KöMaL Problems in Mathematics, November 2016
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on December 12, 2016. |
K. 517. In Normalia, there is a city in which the people called ,,truetellers'' always tell the truth. Those who are not truetellers will tell the truth one day, and then lie on the following day, then also tell the truth, and so on. The last names of Andrew, Barbara, and Cecilia are Small, Large and Long, in some order. Determine the last name of each of them, given their statements below:
on Monday
Andrew: Barbara is not telling the truth.
Barbara: I am not a trueteller.
Cecilia: There is a trueteller among us.
on Tuesday
Andrew: Cecilia told the truth yesterday.
Barbara: Andrew's last name is either Large or Small.
Cecilia: Barbara's last name is not Small.
(6 pont)
solution (in Hungarian), statistics
K. 518. The numbers in the figures and further figures created in the same way are called hexagonal numbers. Without proof, find a formula for the \(\displaystyle n\)th hexagonal number, and use it to show that 2016 is a hexagonal number.
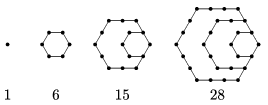
(6 pont)
solution (in Hungarian), statistics
K. 519. In ,,negadecimal'' notation, the place values of the digits of a number are the powers of 10, but with alternating signs, that is, instead of the place values 1, 10, 100, 1000 etc. of decimal notation, they are 1, \(\displaystyle -10\), 100, \(\displaystyle -1000\) etc. For example,
\(\displaystyle 325_{-10} =3 \cdot 100 + 2\cdot (-10) + 5 \cdot 1 = 300 - 20 + 5 = 285_{10}. \)
Represent the number of this year in negadecimal notation.
(6 pont)
solution (in Hungarian), statistics
K. 520. Is it possible to specify six natural numbers, such that by selecting two numbers in every possible way and adding them we should get distinct consecutive natural numbers?
(6 pont)
solution (in Hungarian), statistics
K. 521. In a running race, each participating school entered four runners. Andrew, Ben, Charlie and Dennis were the runners from one school. Andrew finished in the best place out of the four: he finished in the first quarter of all runners participating. Ben came in 18th, followed by Charlie, who was beaten by more than four times as many runners as Andrew. Dennis came in last of the four of them: he finished in the 59th place. How many schools entered students in the running race?
(6 pont)
solution (in Hungarian), statistics
K. 522. Originally, a theatre sold tickets for 1000 forints (HUF, Hungarian currency) a piece for a particular performance. There are 300 seats altogether. Since the full-priced tickets did not sell so well, the theatre issued a coupon. With the coupon, tickets were available for 25% less (so all further customers bought their tickets in this way). The income achieved from the tickets sold for the reduced price was found to be half as much as the income from those with full price. In spite of all these marketing efforts, there were still 50 tickets remaining. For what price should they be sold immediately before the performance so that the total income should reach 80% of the maximum achievable income originally planned?
(6 pont)
 |
Problems with sign 'C'Deadline expired on December 12, 2016. |
C. 1378. One of three real numbers is 2 more than the average of the three numbers. How much greater is that number than the average of the other two?
(5 pont)
solution (in Hungarian), statistics
C. 1379. A certain cyclic trapezium has an inscribed circle. Prove that one of the two line segments joining the points of tangency on the opposite sides is the geometric mean of the bases, and the other is the harmonic mean.
(5 pont)
solution (in Hungarian), statistics
C. 1380. An odd number of digits are written on the circumference of a circle. Each of them is a 0, 1 or 2, and they are not all equal. In each step, we simultaneously write between every pair of adjacent numbers the remainder of their sum divided by 3, and then erase the original two numbers. Is it possible that all numbers become identical on the circumference of the circle after a few such steps?
Proposed by D. Matolcsi, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1381. Let \(\displaystyle M\) denote the intersection of the line of the altitude drawn from vertex \(\displaystyle A\) of an acute-angled triangle \(\displaystyle ABC\) with the Thales' circle of \(\displaystyle BC\). Let \(\displaystyle N\) be the intersection of the altitude from vertex \(\displaystyle C\) with the Thales' circle of \(\displaystyle AB\). Prove that \(\displaystyle |BM|=|BN|\).
(5 pont)
solution (in Hungarian), statistics
C. 1382. Prove the following inequality:
\(\displaystyle \frac{1}{1+\sqrt2}+\frac{1}{\sqrt2+\sqrt3}+\frac{1}{\sqrt3+\sqrt4}+\ldots +\frac{1}{\sqrt{2016}+\sqrt{2017}}< \sqrt{2017}\,. \)
(5 pont)
solution (in Hungarian), statistics
C. 1383. The midpoint of line segment \(\displaystyle AB\) is \(\displaystyle O\), the point closer to \(\displaystyle A\) dividing \(\displaystyle AB\) into a ratio \(\displaystyle 1:4\) is \(\displaystyle C\), and the point closer to \(\displaystyle B\) dividing \(\displaystyle AB\) into a ratio \(\displaystyle 1:4\) is \(\displaystyle D\). The perpendiculars drawn at points \(\displaystyle C\), \(\displaystyle O\) and \(\displaystyle D\) to the line segment \(\displaystyle AB\) intersect the semicircle of diameter \(\displaystyle AB\) at the points \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\), respectively. Determine the angles of triangles \(\displaystyle PQB\) and \(\displaystyle QRB\).
Proposed by B. Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1384. Let \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) and \(\displaystyle d\) denote pairwise different positive integers. Solve the following simultaneous equations:
\(\displaystyle ab = c+d,\)
\(\displaystyle a+b = cd.\)
Proposed by Á. Kertész
(5 pont)
 |
Problems with sign 'B'Deadline expired on January 10, 2017. |
B. 4822. Find all natural numbers \(\displaystyle p\) for which the equation \(\displaystyle x^2+(p+2015)x +2016p+1=0\) has an integer solution.
Proposed by T. Jakab, Sepsiszentgyörgy
(3 pont)
solution (in Hungarian), statistics
B. 4823. In an acute-angled triangle \(\displaystyle ABC\) (\(\displaystyle AB < AC\)), the foot of the altitude from vertex \(\displaystyle A\) is \(\displaystyle D\), and the centre of the circumscribed circle is \(\displaystyle O\). Prove that if the exterior angle bisector of \(\displaystyle BAC\sphericalangle\) is parallel to \(\displaystyle OD\), then the diagonals of the quadrilateral \(\displaystyle AODC\) are equal.
Hungarian Mathematics Competition of Transsylvania
(3 pont)
solution (in Hungarian), statistics
B. 4824. Let \(\displaystyle x\) and \(\displaystyle y\) be real numbers for which \(\displaystyle xy=1\). Determine the largest and smallest values of the expression
\(\displaystyle K=\frac{{(x+y)}^2-(x-y)-2}{{(x+y)}^2+(x-y)-2}. \)
Proposed by J. Szoldatics, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 4825. Problem B. 4825. was already proposed earlier this spring, therefore we replace it with a new problem to be submitted together with the problems in this December issue. We apologize for any inconvenience.
Let us consider the concave hexagon in the figure: the points \(\displaystyle ABCD\) form a unit square, and the triangle \(\displaystyle AEF\) is isosceles, with base length equal to two and one angle equal to \(\displaystyle 135^{\circ}\). By using a single slice, cut the hexagon into two equal pieces. Demonstrate the correctness of your solution.
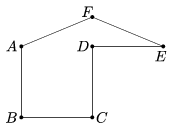
(4 pont)
solution (in Hungarian), statistics
B. 4826. The circles \(\displaystyle a\) and \(\displaystyle b\) intersect at two distinct points \(\displaystyle P\) and \(\displaystyle Q\). Suppose that \(\displaystyle A_0\) is a point that lies on circle \(\displaystyle a\). Define the points \(\displaystyle B_0\), \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle A_2\) etc., respectively, as follows: \(\displaystyle B_i\) is the intersection of line \(\displaystyle A_iP\) with \(\displaystyle b\), and then \(\displaystyle A_{i+1}\) is the intersection of line \(\displaystyle B_iQ\) with \(\displaystyle a\). (If \(\displaystyle A_i = P\) then line \(\displaystyle A_iP\) means the tangent of circle \(\displaystyle a\) at \(\displaystyle P\), and if \(\displaystyle B_i = Q\) then line \(\displaystyle B_iQ\) means the tangent of circle \(\displaystyle b\) at \(\displaystyle Q\).) Show that if there exists an \(\displaystyle A_n\) (\(\displaystyle n\ge 2\)) for which \(\displaystyle A_0\) and \(\displaystyle A_n\) coincide, then this holds for any point \(\displaystyle A_0\) of circle \(\displaystyle a\).
Proposed by K. Williams, Szeged
(4 pont)
solution (in Hungarian), statistics
B. 4827. Suppose that \(\displaystyle p\) is a polynomial of integer coefficients, not identically 0, such that \(\displaystyle p(n)\) is divisible by 2016 for all integers \(\displaystyle n\). What is the minimum possible value of the sum of the absolute values of the coefficients of \(\displaystyle p\)?
(5 pont)
solution (in Hungarian), statistics
B. 4828. Let \(\displaystyle 0<x_1<x_2<\ldots<x_n<2\pi\). Show that
\(\displaystyle \sum_{i,j=1;\; i\ne j}^n \frac{1}{|x_i-x_j|}+\frac{1}{2\pi-|x_i-x_j|}\ge \frac{n^2}{\pi}\sum_{k=1}^{n-1} \frac 1k. \)
On what condition will the equality hold?
(6 pont)
solution (in Hungarian), statistics
B. 4829. Cover the surface of the unit sphere with great circles, such that every point is contained in at most four great circles.
(5 pont)
solution (in Hungarian), statistics
B. 4830. Solve the following equation in the set of positive integers:
\(\displaystyle n!=2^a+2^b. \)
Proposed by K. Williams, Szeged
(4 pont)
 |
Problems with sign 'A'Deadline expired on December 12, 2016. |
A. 680. Let \(\displaystyle M(x)\) be a real polynomial having no real root. Prove that for every real polynomial \(\displaystyle P(x)\) there exists a real polynomial \(\displaystyle Q(x)\) such that \(\displaystyle P{(x)}^2+Q{(x)}^2\) is divisible by the polynomial \(\displaystyle M(x)\).
Based on a problem of the Miklós Schweitzer competition
(5 pont)
solution (in Hungarian), statistics
A. 681. The positive numbers \(\displaystyle a_1,a_2,\ldots,a_n\) satisfy \(\displaystyle \sqrt{a_1}+\sqrt{a_2} +\cdots+\sqrt{a_n}=1\). Show that
\(\displaystyle {a_1}^{a_1}\cdot {a_2}^{a_2}\cdot \ldots \cdot {a_n}^{a_n} \ge {(a_1+a_2+\ldots+a_n)}^2. \)
(5 pont)
solution (in Hungarian), statistics
A. 682. Let \(\displaystyle A_1B_1C_1D_1E_1F_1A_2B_2C_2D_2E_2F_2\) be a cyclic dodecagon such that its diagonals \(\displaystyle A_1A_2\), \(\displaystyle B_1B_2\) and \(\displaystyle C_1C_2\) are concurrent, the diagonals \(\displaystyle A_1A_2\), \(\displaystyle E_1E_2\) and \(\displaystyle F_1F_2\) are concurrent, the diagonals \(\displaystyle C_1C_2\), \(\displaystyle D_1D_2\) and \(\displaystyle E_1E_2\) are concurrent, and finally the diagonals \(\displaystyle B_1B_2\), \(\displaystyle D_1D_2\) and \(\displaystyle F_1F_2\) are concurrent.Let \(\displaystyle k_A\), \(\displaystyle k_C\) and \(\displaystyle k_E\) be three circular arcs in the interior of the dodecagon's circumcircle such that \(\displaystyle k_A\) connects \(\displaystyle A_1\) and \(\displaystyle A_2\), \(\displaystyle k_C\) connects \(\displaystyle C_1\) and \(\displaystyle C_2\), and \(\displaystyle k_E\) connects \(\displaystyle E_1\) and \(\displaystyle E_2\). Let the intersection points of the three arcs be \(\displaystyle B=k_A\cap k_C\), \(\displaystyle D=k_C\cap k_E\) and \(\displaystyle F=k_A\cap k_E\). Prove that the circular arcs \(\displaystyle B_1BB_2\), \(\displaystyle D_1DD_2\) and \(\displaystyle F_1FF_2\) are concurrent. (These arcs degenerate to line segments if their specified points are collinear.)
Marcello Mamino, Dresden, Luca Ghidelli, Ottawa and Ilya Bogdanov, Moscow
(5 pont)
Upload your solutions above.
