KöMaL Problems in Mathematics, January 2017
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 10, 2017. |
K. 529. Four circles are arranged as shown in the figure. The numbers \(\displaystyle 1, 2, 3, \ldots, 10\) are to be written in the ten regions formed by the circles such that the sum of the numbers within each circle is the same. What is the largest possible value of that sum?
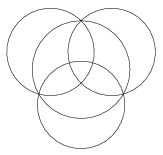
(6 pont)
solution (in Hungarian), statistics
K. 530. Anthony és Blasius inherited a plot of land from their father. They divided it between themselves as instructed by the last will of the father. Each son grew only wheat and corn on this plot. Since the soil is more suitable for corn, a particular area used for growing wheat will only yield one third as much as the same area used for growing corn on it. Anthony produced one and a half as much wheat as corn, while Blasius produced five times as much corn as wheat. The ratio of the yield of wheat to corn for the entire plot was \(\displaystyle 11:27\). In what proportion did the two sons inherit the land?
(6 pont)
solution (in Hungarian), statistics
K. 531. Let us consider a \(\displaystyle 4\times 4\) chessboard. In each step, the colour of every square in a chosen \(\displaystyle 2\times 2\) block is changed (black to white, and white to black).
\(\displaystyle a)\) By performing some of these steps, is it possible to obtain a completely black board?
\(\displaystyle b)\) Is this possible in the case of a \(\displaystyle 5\times 5\) board, provided that the corners are initially white?
(6 pont)
solution (in Hungarian), statistics
K. 532. Greg charges the battery of his cell phone every night, so he can start every new day with a 100% charged battery. If he only uses the phone for talking, the battery lasts 30% longer than when he plays games with it, and it lasts 60% longer than when he is surfing the net. Today, he has talked for 20 minutes on the phone, played for 50 minutes, and spent 80 minutes on the net. The battery is now flat. How long may Greg use the internet with his phone if it is fully charged, and he does not use it for anything else?
(6 pont)
solution (in Hungarian), statistics
K. 533. May the sum of the squares of four consecutive natural numbers be a perfect square?
(6 pont)
solution (in Hungarian), statistics
K. 534. Kate has a round table, it is a circle of area 4 m\(\displaystyle {}^{2}\). She also has a circular tablecloth of exactly the same size to go with it. Joe has a square table, two metres on a side, and a square tablecloth of the very same size. One day, the two of them switched the tablecloths. Each of them laid the other's tablecloth on their own table, with the centre of the cloth carefully positioned on the centre of the table. Each observed that the tablecloth overhung the edge of the table at some places, while the table remained partly uncovered. In which case was the area of the uncovered part greater?
(6 pont)
 |
Problems with sign 'C'Deadline expired on February 10, 2017. |
C. 1392. The number \(\displaystyle 2017-(2+0+1+7)\) is divisible by the number \(\displaystyle (2+20+201)\), that is, 2017 has the following property: if the sum of the digits of the number is subtracted from it, the result will be a four-digit number that is divisible by the sum of the one-digit number formed by the first digit, the two-digit number formed by the first two digits, and the three-digit number formed by the first three digits. How many four-digit numbers have this property?
(5 pont)
solution (in Hungarian), statistics
C. 1393. Prove that there is no triangle whose altitudes have lengths 20, 17 and 9 cm.
(5 pont)
solution (in Hungarian), statistics
C. 1394. How many positive integers are there whose prime factorization contains only the two smallest primes, and whose third power has eight times as many positive divisors as the number has?
(Matlap, Kolozsvár)
(5 pont)
solution (in Hungarian), statistics
C. 1395. The length of one side of a parallelogram \(\displaystyle ABCD\) is twice the length of the other side. Determine the ratio of the area of the parallelogram formed by the interior angle bisectors to the area of \(\displaystyle ABCD\).
(5 pont)
solution (in Hungarian), statistics
C. 1396. All through a football game, a record of the current score is kept and updated. How many different records are possible if the final result is 3-3? In what percentage of the possible records is there a part of the game when one team was leading by at least 2 goals?
(5 pont)
solution (in Hungarian), statistics
C. 1397. Prove that the function
\(\displaystyle f\colon \mathbb{R}\to \mathbb{R},\quad x\mapsto \begin{cases} 2x+2-6k, & \text{if \ } x\in \left[6k; 6k+2\right[ ,\\ \frac{x-2+6k}{2}, & \text{if \ } x\in \left[6k+2; 6k+6\right[ \end{cases} \quad (k\in \mathbb{Z}) \)
(where \(\displaystyle k\) takes every integer value) is one-to-one and equal to its own inverse.
(5 pont)
solution (in Hungarian), statistics
C. 1398. A cube is inscribed in a right circular cone: one face lies on the base of the cone, and the remaining four vertices are on the lateral surface of the cone. What is the surface area of the cube if the base radius of the cone is \(\displaystyle \frac{\sqrt{3}}{2}\,\), and its slant height is three times as large?
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 10, 2017. |
B. 4840. Show that every integer can be represented in the form \(\displaystyle x^{2}+y^{2}-z^{2}\) with appropriate positive integers \(\displaystyle x\), \(\displaystyle y\), \(\displaystyle z\).
(3 pont)
solution (in Hungarian), statistics
B. 4841. The circle \(\displaystyle k\) centred at \(\displaystyle O\) intersects line \(\displaystyle e\) at points \(\displaystyle A\) and \(\displaystyle B\), and it intersects the perpendicular bisector of line segment \(\displaystyle OB\) at points \(\displaystyle C\) and \(\displaystyle D\). Prove that the angle bisector of angle \(\displaystyle COA \sphericalangle\) and line \(\displaystyle e\) enclose an angle of 60 degrees.
(3 pont)
solution (in Hungarian), statistics
B. 4842. Let \(\displaystyle p\) denote an arbitrary (positive) prime number. Find all positive integers \(\displaystyle b\) such that the roots of the quadratic \(\displaystyle x^2-bx+bp = 0\) are integers.
(Proposed by Á. Lelkes, New York City)
(4 pont)
solution (in Hungarian), statistics
B. 4843. The escribed circles drawn to sides \(\displaystyle AC\) and \(\displaystyle BC\) of a triangle \(\displaystyle ABC\) touch the sides at points \(\displaystyle K\) and \(\displaystyle L\), respectively. Prove that the line passing through the midpoints of line segments \(\displaystyle KL\) and \(\displaystyle AB\) is parallel to the angle bisector of \(\displaystyle ACB\sphericalangle\), and it halves the perimeter of the triangle.
(Based on a Kvant problem)
(5 pont)
solution (in Hungarian), statistics
B. 4844. Find all ordered triples \(\displaystyle (p,q,n)\) (where \(\displaystyle n\ge 2\) is a positive integer) such that there exist exactly \(\displaystyle n\) real numbers, not necessarily different, whose product is \(\displaystyle p\) and whose sum is \(\displaystyle q\).
(Proposed by I. Porupsánszki, Miskolc)
(5 pont)
solution (in Hungarian), statistics
B. 4845. Prove that each term of the sequence
\(\displaystyle a_1 =1,\)
\(\displaystyle a_n =\frac{4a_{n-1}+\sqrt{7a^2_{n-1}-3}}{3};\quad n\ge2\)
is rational.
(Proposed by J. Szoldatics, Budapest)
(5 pont)
solution (in Hungarian), statistics
B. 4846. The intersection of five closed half planes is bounded. Show that it is possible to select four out of them such that their intersection is also bounded.
(4 pont)
solution (in Hungarian), statistics
B. 4847. Let \(\displaystyle f\) be a positive bounded function defined on the interval \(\displaystyle [0;1]\). Prove that there are numbers \(\displaystyle x_1\) and \(\displaystyle x_2\) for which
\(\displaystyle \frac{(x_2-x_1)f^2(x_1)}{f(x_2)} >\frac{f(0)}4. \)
(O. Reutter, Germany)
(6 pont)
solution (in Hungarian), statistics
B. 4848. Find all convex polyhedra \(\displaystyle P\) whose interior contains a point \(\displaystyle O\) such that every plane passing through \(\displaystyle O\) intersects \(\displaystyle P\) in a parallelogram centred at \(\displaystyle O\).
(6 pont)
 |
Problems with sign 'A'Deadline expired on February 10, 2017. |
A. 686. In the triangle \(\displaystyle ABC\), the incircle is denoted by \(\displaystyle \omega\). The excircle opposite to \(\displaystyle A\) is tangent to the line \(\displaystyle BC\) at point \(\displaystyle A_1\). Let \(\displaystyle X\) be an arbitrarily chosen point on the extension of the segment \(\displaystyle AA_1\) beyond \(\displaystyle A_1\), and let the line \(\displaystyle BC\) meet the tangents drawn from \(\displaystyle X\) to \(\displaystyle \omega\) at \(\displaystyle Y\) and \(\displaystyle Z\), such that \(\displaystyle BY<BZ\). Show that \(\displaystyle XY-XZ\) does not depend on the position of the point \(\displaystyle X\).
(Russian problem)
(5 pont)
solution (in Hungarian), statistics
A. 687. Let \(\displaystyle f(x)\) and \(\displaystyle g(x)\) be nonzero polynomials such that the degree of \(\displaystyle f(x)\) is higher than that of \(\displaystyle g(x)\). Suppose that for infinitely many prime numbers \(\displaystyle p\), the polynomial \(\displaystyle pf(x)+g(x)\) also has a rational root. Show that \(\displaystyle f(x)\) has a rational root.
(Italian problem)
(5 pont)
A. 688. Prove that among any \(\displaystyle {\color{red}4097}\) distinct \(\displaystyle 0\)–\(\displaystyle 1\) sequences of length \(\displaystyle 24\), there are two which differ from each other at no more than \(\displaystyle 7\) positions.
(Brazilian problem)
(5 pont)
Upload your solutions above.
