| [103] Hajba Károly | 2003-11-24 10:08:25 |
 Megoldás a 23. feladatra:
Legyen (S) a négyzetbe írandó számok összege és (K) az egy sor-oszlop-átló összege. Végezzük el a következő műveletet:
A két átló kétszereséhez adjuk hozzá a középső oszlop és sort és vonjuk ki belőle a szélső oszlopokat és sorokat. Így egyrészről a középső elem 6-szorosát, mésrészről 2*K-t kaptunk. Tehát a középső elem 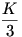 ill. ill. 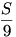 -cel egyenlő. -cel egyenlő.
A mi esetünkben a középső szám 5 és K=15. Mivel mindkét szám páratlan, így az egy sor-oszlop-átlóba írandó másik két szám vagy mindkettő páros vagy mindkettő páratlan. Továbbá az oszlopok és sorok szélső elemeinek összege páratlan, ez vagy 3 páratlan, vagy 2 páros és 1 páratlan szám összege. Ebből következik, hogy a 4 páros szám csak a sarkokba kerülhet.
A bűvös négyzetnél a nem egy sor-oszlop-átlóba írt 3 szám, mely egyéb keretfeltételeknek is megfelel, egyértelműen meghatározza a többi számot. Így a négy sarokszámot kétféle irányultsággal tudom beírni, hogy ne lehessen egymásba forgatni. Ha a tükrözéssel kialakult állapotot is azonosnak tekintjük, csak egy megoldás létezik. Tehát a megoldás az alábbi és a tükörképe:
Hajba Károly
|
| Előzmény: [102] lorantfy, 2003-11-23 09:15:26 |
|
| [102] lorantfy | 2003-11-23 09:15:26 |
 23.a) feladat Írd be az 1,2,3,4,5,6,7,8,9 számokat egy 3x3 bűvös négyzetbe!
(Úgy, hogy a sorok, oszlopok és átlók összege is azonos legyen.)
| .... |
. |
. |
| . |
.... |
. |
| . |
. |
.... |
|
23.b) feladat Hányféle beírás lehetséges, ha az egymásba forgathatókat nem tekintjük különbözőnek?
(Elemi forgatás (45 fok): amikor a főátló (....) oszlopba, a másik sorba megy át.)
|
|
| [101] Hajba Károly | 2003-11-21 13:46:46 |
 Kedves Lajos!
A pozitív egész számok tartományában értelmeztem és a 2. sor első számának 1-gyel kell kezdődnie és legalább 2 jegyű. Továbbá mind a 8 összeg egyenlő.
László pontosítása után természetesen csak egy létezik. A középső száma: 107, összege: 321
Hajba Károly
|
| Előzmény: [99] Lóczi Lajos, 2003-11-21 11:06:19 |
|
| [100] lorantfy | 2003-11-21 11:28:15 |
 Kedves Lajos és Károly!
Elnézést, de elfelejtettem írni a BŰVÖS NÉGYZET-hez, hogy a pontok csak helykitöltő szerepet játszanak, különben összeesik a TeX tábla. Szóval gondom volt az üres rekeszekkel és így tudtam gyorsan megoldani. A beírt számok: 1, 19, 98. (Az 1 számjegy mellett szintén csak "helynövelő" a pont.)
|
| Előzmény: [99] Lóczi Lajos, 2003-11-21 11:06:19 |
|
| [99] Lóczi Lajos | 2003-11-21 11:06:19 |
 Kedves Onogur!
Attól függ, hogyan értjük a kérdést.
Pontosan milyen feltételekkel kaptál kilenc megoldást? Gondolom, a négyzet sor- és oszlopösszegei ugyanaz a szám, de a fő- és mellékátlók összege is ez? A pontok egy számjegyet jelölnek? Negatív értékek megengedettek?
|
| Előzmény: [98] Hajba Károly, 2003-11-21 10:21:01 |
|
|
| [97] SchZol | 2003-11-20 16:23:38 |
 Kedves Suhanc!
Igen a nehezítésben meghagytam a feltételt, és van rá megoldásom! Egyébként, ha benézel a Biliárdgolyók és más méricskélős feladatok című téma alá, ott megtalálod Lorantfy megoldását.
Üdv, Zoli
|
| Előzmény: [96] Suhanc, 2003-11-20 14:54:09 |
|
| [96] Suhanc | 2003-11-20 14:54:09 |
 Üdvözlet! Ha jól láttam, a 15. feladatra még senki nem írt megoldást. Van egy ötletem, de az megszegi azt a kikötést,ami még az 5. feladatban szerepelt, névszerint: minden ládában 1000 pénzérme van. Sch Zolitól kérdezném: a nehezítésben meghagytad ezt a feltételt? Ha igen, van megoldásod rá?
|
|
| [95] lorantfy | 2003-11-19 22:39:21 |
 Egy könnyed kis feladat. A 7. osztályos fiamnak volt valamelyik versenyen.
Töltsétek ki a bűvös négyzetet!
|
|
|
| [93] jenei.attila | 2003-11-19 13:00:17 |
 Úgy gondolom, ez a feladat nem különbözik a négyzet szerkesztésétől, ugyanis mindkét esetben adott egység mellett a négyzetgyök(2) hosszúságú szakaszt kell megszerkeszteni csak körző segítségével. Bármelyik feladat megoldása megoldja a másikat is.
|
| Előzmény: [92] Hajba Károly, 2003-11-19 00:54:04 |
|
|
| [91] Kós Géza | 2003-11-18 22:50:54 |
 A 18-szöges megoldást is nézzük meg, szerintem nagyon tanulságos.
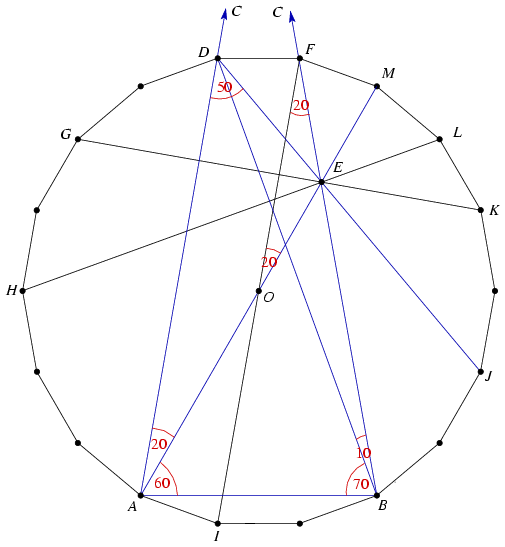
A szabályos 18-szögnek két nagy előnye van. Az egyik, hogy az átlók és oldalak közötti szögek mindig a 10o többszörösei, ezért esélyünk van megtalálni a feladat ábráját az átlók között. A másik, hogy sok olyan pont van a belsejében, ahol nagyon sok átló megy át. Az ábrán az E egy ilyen pont.
Legyen E először csak az AM átmérő és DJ metszéspontja. A DJ tükörképe az AM egyenesre KG, tehát KG is átmegy E-n. A KG egy nagyon speciális átló, a hozzá tartozó középponti szög éppen 120o. Ebből következik, hogy az O és F pontok egymás tükörképei a KG átlóra. Az OM egyenes tükörképe a KG átlóra éppen FB, mert O tükörképe F, és az irányok is stimmelnek. Tehát FB is átmegy E-n. Végül HL az FB tükörképe az AM átmérőre, tehát ez is átmegy E-n.
|
 |
| Előzmény: [63] Kós Géza, 2003-11-13 14:25:51 |
|
| [90] lorantfy | 2003-11-18 20:45:43 |
 Kedves Péter Pál!
Gratulálok! Jó a megoldás. Annyi vari lehet, hogy az első menetben egy kannibál és egy fehérember megy át és a fehérember hozza vissza a csónakot. Én már előre megcsináltam táblázatban, hogy gyakoroljam a TeX táblát:
| 3K |
3F |
|
|
|
| 2K |
2F |
F,K > |
|
|
| 2K |
2F |
< F |
K |
|
|
3F |
K,K > |
K |
|
|
3F |
< K |
2K |
|
| K |
F |
F,F > |
2K |
|
| K |
F |
< K,F |
K |
F |
| 2K |
|
F,F> |
K |
F |
| 2K |
|
< K |
|
3F |
| K |
|
K,K > |
|
3F |
| K |
|
< K |
K |
3F |
|
|
K,K > |
K |
3F |
|
|
|
3K |
3F |
|
|
| Előzmény: [89] Pach Péter Pál, 2003-11-17 21:37:15 |
|
| [89] Pach Péter Pál | 2003-11-17 21:37:15 |
 Megoldást írok a 18. feladatra:
1. lépés: Átmegy két kannibál, egyikük a túlparton marad, másikuk visszahozza a csónakot.
2. lépés: Ugyanez még egyszer.
3. lépés: Átmegy két fehérember, egyikük ott marad, másikuk viszont egy kannibál társaságában visszatér.
4. lépés: Átkel a még hátralévő két fehérember, a túlparti kannibál visszaviszi a csónakot.
5-6. lépés: Most már csak az van hátra, hogy a kannibálok is átkeljenek. Először átkelnek ketten, majd egyikük visszmegy a harmadikért.
Könnyen végiggondolhatjuk, hogy a kannibálok az átkelés során sosem kerültek többségbe. Ez azt jelenti, hogy mindannyiukat sikerült – épségben – átjuttatnunk a túlpartra.
|
| Előzmény: [79] lorantfy, 2003-11-16 17:50:10 |
|
| [88] Pach Péter Pál | 2003-11-17 21:34:00 |
 Trükkös a megoldásod, BrickTop. Egyébként nem szükséges, hogy a két ponton átmenő egyenes is adott legyen. Leírok egy megoldást, ami csak a két pont (és természetesen a körző megfelelő használatának) ismeretét feltételezi
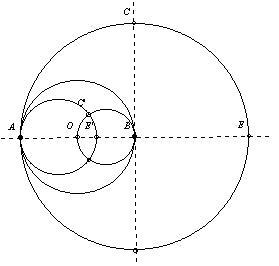
A 20. feladat II. megoldása következik: Könnyen bizonyítható, hogy körző segítségével (vonalzó nélkül) tudunk invertálni egy pontot egy olyan körre, aminek a középpontját is ismerjük. (Ezt először külső pontra érdemes belátni.) Aki nem ismeri, gondolkozzon el rajta.
A két pont, amihez négyzetet akarunk rajzolni, legyen A és B!(A keresett négyzet ABCD.) AB-hez háromszögrácsot rajzolva megkapjuk A tükörképét B-re: E-t. Most E-t invertáljuk az A középpontú, AB sugarú körre, a képe az AB szakasz felezőpontja, O lesz. Az O középpontú, 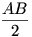 sugarú kör legyen k. C-t megkaphatjuk a B középpontú, AB sugarú kör, és a B-ben AB egyenesére állított merőleges egyenes (egyik) metszéspontjként. Ha ezt a két alakzatot invertáljuk k-ra, akkor az egyenesből is kör lesz, és így már meg tudjuk szerkeszteni metszéspontjukat. A körünk képe az AE’ átmérőjű kör, ahol E’ az E pont képe, ugyanis O illeszkedik AE-re. (Ezt a kört meg tudjuk rajzolni, hiszen felezőpontját megszerkeszthetjük ugyanúgy, ahogy AB felezőpontját megszerkesztettük. Az egyenesünk képe a BO átmérőjű kör. sugarú kör legyen k. C-t megkaphatjuk a B középpontú, AB sugarú kör, és a B-ben AB egyenesére állított merőleges egyenes (egyik) metszéspontjként. Ha ezt a két alakzatot invertáljuk k-ra, akkor az egyenesből is kör lesz, és így már meg tudjuk szerkeszteni metszéspontjukat. A körünk képe az AE’ átmérőjű kör, ahol E’ az E pont képe, ugyanis O illeszkedik AE-re. (Ezt a kört meg tudjuk rajzolni, hiszen felezőpontját megszerkeszthetjük ugyanúgy, ahogy AB felezőpontját megszerkesztettük. Az egyenesünk képe a BO átmérőjű kör.
A két kapott kör metszéspontjai közül az egyik C’, vagyis C képe. Ha C’-t invertáljuk k-ra, akkor megkapjuk a keresett C pontot. Természetesen D ugyanígy kapható meg.
A 20. feladat speciális esete a Mohr-Mascheroni-tételnek, ami a következő állítást bizonyítja: „Minden körzővel és vonalzóval elvégezhető szerkesztés elvégezhető csak körző segítségével is.” Erről, és még számos híres matematikai problémáról olvashatunk Heinrich Dörrie: A diadalmas matematika c. könyvében. (Szóval ez most egyben könyvajánlás is!) A könyvet egyébként az egyik matektanárunk, Hraskó András ajánlotta.
|
 |
| Előzmény: [87] BrickTop, 2003-11-17 20:48:41 |
|
| [87] BrickTop | 2003-11-17 20:48:41 |
 20. feladat, megoldás: Adott A és B pont.
1) A-ból és B-ből körívezünk AB-vel --> C metszéspont.
2) A-ból és C-ből körívezünk AB-vel --> D metszéspont.
3) A-ból és D-ből körívezünk AB-vel --> E metszéspont.
4) E-ből körívezünk BD-vel --> F metszéspont az AB szakaszon.
5) B-ből körívezünk BE-vel, D-ből körívezünk FB-vel --> G a két körív metszéspontja (a két körív valójában érinti egymást).
6) F-ből körívezünk EG-vel --> a keletkezett körív és a B középpontú, AB sugarú körív (ld. 1)) metszéspontja a négyzet harmadik pontja, H.
7) H-ből körívezünk AB-vel :) --> a keletkezett körív és az A középpontú, AB sugarú körív (ld. 1)) metszéspontja a négyzet negyedik pontja.
Kicsit több, mint egy éve jöttem rá erre a megoldásra. Most megprobáltam szerkesztéssel ellenőrizni, nem nagyon jött ki, de biztos azért, mert bénán szerkesztek. Elméletileg szerintem jó. Bizonyítást nem írtam, mert ha megvan az ábra, már nagyon egyszerű belátni, hogy a négyzet pontjait kapjuk. Ábrát nem készítettem, mert lusta voltam (órákig tartana egy ilyen ábrát megcsinálni az én programarzenálommal), és mert az ábra lelövi a poént. Így aki meg akarja oldani a feladatot, egyszerűen nem olvassa el a szerkesztés menetét.
Remélem nem néztem el semmit és nem vesztegettem el negyed órát egy hibás szerkesztés leírásával :)
|
| Előzmény: [86] SchZol, 2003-11-17 20:07:20 |
|
|
| [85] BrickTop | 2003-11-17 18:32:42 |
 A 20. feladatban a 2 pont nincs véletlenül összekötve? Mert nekem van megoldásom, de csak ha egy szakasz van megadva (tehát 2 pont ami össze van kötve).
|
| Előzmény: [84] SchZol, 2003-11-17 17:14:16 |
|
| [84] SchZol | 2003-11-17 17:14:16 |
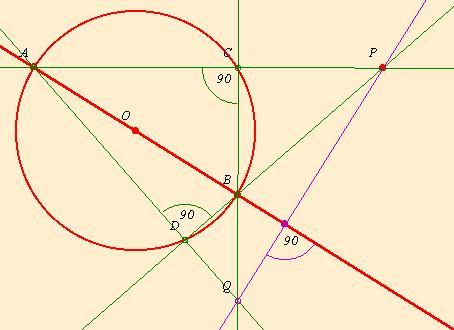
 PQ azért merőleges AB-re, mert PAQ háromszögben QC és PD magasságvonal, tehát B a PAQ háromszög magasságpontja, ebből következik, hogy AB egyenes is magassága a PAQ háromszögnek, tehát merőleges AB PQ-ra.
20.feladat: Adott két pont. Egyetlen körző segítségével rajzoljunk négyzetet, melynek e két pont két szomszédos csúcsa.
|
| Előzmény: [83] lorantfy, 2003-11-17 16:41:14 |
|
| [83] lorantfy | 2003-11-17 16:41:14 |
 Mivel csak vonalzót használhatunk mást nem is tehetünk csak összekötünk két pontot. PA majd PB. Ezek metszik a kört C és D pontokban. Ezután CB, AD ezek metszik egymást Q-ban.
Bizonyítandó: PQ egyenes merőleges AB-re!
|
 |
| Előzmény: [82] jenei.attila, 2003-11-17 15:32:04 |
|
| [82] jenei.attila | 2003-11-17 15:32:04 |
 Kedves László!
Köszönöm a szép ábrát, kicsit reméltem is, hogy lesz türelmed megrajzolni. Maradva a geometriánál, egy nem túl nehéz de érdekes feladat: adva van egy kör, a középpontján átmenő egyenes, és egy pont a körön és egyenesen kívül. Egy egyenes vonalzó használatával szerkesszünk a ponton átmenő, egyenesre merőleges egyenest.
|
| Előzmény: [81] lorantfy, 2003-11-17 15:15:00 |
|
|
| [80] jenei.attila | 2003-11-17 13:18:39 |
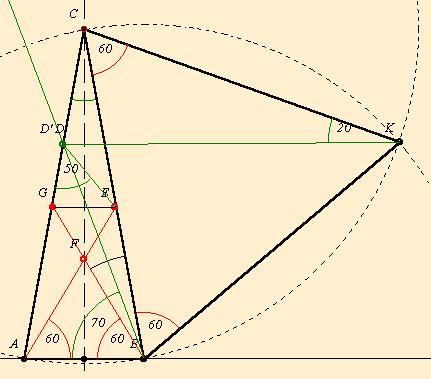
 Utoljára az általam feladott háromszöges feladatról. Csillag megoldása ABD szög=50 fok esetére ismét nagyon ötletes és egyszerű. Én jóval körülményesebben oldottam meg, mégis leírom, mert megoldja az ABD=70 fok esetet is. Tehát: Szerkesszünk a BC oldalra kifelé szabályos háromszöget, amelynek harmadik csúcsa legyen K. A D´ pontot AC-n vegyük fel úgy, hogy CKD´ szög=20 fok legyen. Megmutatjuk, hogy ekkor D és D´ egybeesik. Valóban, mivel D´CK szög=80 fok és CKD´=20 fok, ezért CD´K=80 fok és KC=KD´=KB. A D´KB szög=40 fok, ezért (és KD´=KB miatt) KBD´ szög=70 fok. De KBD szög is =70 fok, ezért D´=D. Megállapítottuk tehát, hogy a CDK háromszög egybevágó az ABC háromszöggel, ezért CD=AB. De GD=GC-CD=GB-CD=GB-AB=GB-FB=GF, és GF=GE miatt GD=GE, amiből GDE=50 fok, és EDB=20 fok.
Az ABD=50 fok esete: D helyett L-lel jelöljük a szóbanforgó pontot, és D maradjon meg az előzőek szerint, tehét ABL szög =50 fok és EDA szög=50 fok. Szintén DC=AB=AL miatt AEL és CED háromszögek egybevágók, ezért EL=ED, de LDE szög =50 fok (D-t most így vettük vel, nem az előző feladatból jött, bár egybeesik vele), DLE szög is = 50 fok, amiből ELB szög =80 fok.
Bocs a hosszú hozzászólásért, legközelebb rövidebb leszek.
|
|
| [79] lorantfy | 2003-11-16 17:50:10 |
 Kedves Fórumosok!
Biztos ismeritek azt a feladatot, hogy vigyük át a farkast a nyulat és a káposztát a folyón, ha a csónakunkban csak egy hely van és a farkas megeszi a nyulat, a nyúl meg a káposztát ha egyedül hagyjuk őket. Ha nem, olvassátok el a Szegény ember káposztája c. Gárdonyi mesét:
http://www.brody.iif.hu/hmek/gardonyi/tihanyi/kaposzta.htm
Ennek egy variációja a következő: 18. feladat:
A folyó egyik partján áll 3 kannibál és 3 fehérember. Egy kétszemélyes csónakjuk van és úgy kell átkelniük a folyón, hogy egyik parton sem lehetnek többségben a kannibálok, mert akkor megeszik a fehérembereket. A csónakban ülő partotérő emberek már partonlévőnek számítanak.
|
 |
|
| [78] Csillag | 2003-11-14 22:27:12 |
 Üdv Mindenkinek!
Azt hiszem jobb lenne, ha ettől a témakörtől elválasztanánk a "divatosabb" témákat: pl. Rubik-kocka, billiárdgolyók,...
Más: a (66)-os hozzászólásomban: nem paralelogramma, hanem deltoid a DFEG négyszög:)
GB
|
|
| [77] toto | 2003-11-14 18:38:51 |
 http://www.superliminal.com/cube/cube.htm
Itt lehet találni egy virtuális, négydimenziós 3x3x3x3-as kockát. Nem volt időm megnézni, de lehet olyan érdekes, mint egy 4x4x4 es
|
| Előzmény: [71] SchZol, 2003-11-14 05:48:40 |
|
| [76] Bubu | 2003-11-14 17:32:18 |
 Üdvözletem! Csatlakoznék a kockás cikk kérőihez. Másrészt elmélkedtem a saját problémámon (a 2 hibás golyó esete), az mindenesetre biztosnak tűnik, hogy teljes általánosságban nem megoldható. Úgyhogy a feladat része lett az is, hogy találjuk ki a feladatot:) Egyébként nagyon tetszik a fórum, kár hogy egyelőre kevesen vagyunk. Remélem hamar híre megy, és akkor akár komolyabb problémák is szóba jöhetnek - mint anno a levélváltások...:))
Bubu
|
|
| [75] Hajba Károly | 2003-11-14 13:12:31 |
 Kedves László!
A geodéták, mikor a tervezési alaptérképhez a térképet digitalizálják a meglévő kézzel, tustollal rajzolt állapotról, egyszerűen csak azt mondják: 'bedigizem neked a térképet'. Nem azt mondom, hogy szép, de mindenképpen rövid és már egyes helyeken használják.
Károly
|
| Előzmény: [73] lorantfy, 2003-11-14 12:56:58 |
|
| [74] Hajba Károly | 2003-11-14 13:01:02 |
 Visszatérek a biliárdgolyós feladathoz, mivel úgy tűnik számomra, még sok érdekes dolgot lehet kihozni belőle.
- [39] hozzászólásbeli Gáti Baetrix Zoltán által közzétett táblázata a nehezebb változatnak éppen nem felel meg, de ha a 3. mérésben a 8-as golyót a 12-esre cseréljük, már tökéletes.
- [52]-beli Bubu hozzászólásában a több eltérő golyó felé általánosít. Bennem pedig már korábban felmerült egy másik általánosítási lehetőség, miszerint valamely golyó(k)ról állítjuk, hogy nem tér el és ez alapján, hogy változik a mérhető golyók száma. Továbbá mi a helyzet a kevesebb ill. több mérési számok esetén.
16. feladat: Ha n a mérések száma, mennyi a legnagyobb g(n) golyók száma, mely esetén még meghatározható a hibás golyó és annak eltérése is?
17. feladat: Ha 2-szer mérhetünk, hány biztosan nem hibás golyót kell ismernünk, hogy a lehető legtöbb ismeretlen golyó közül tudjuk kiválasztani az egyetlen hibás golyót és eltérését?
Hajba Károly
|
|
| [73] lorantfy | 2003-11-14 12:56:58 |
 Kedves Károly, Zoli és Kockarajongók!
Feltúrtam a fizika szertárt és megtaláltam a Fizikai Szemle 82/2-es számában a cikket. Jövő héten beszkennelem és recognitázom - szóval nyomtatott formából elektronikus formába alakítom. (Jó lenne erre egy egyszerű szó - a digitalizálni talán nem a legszerencsésebb - ha tudtok jobbat írjátok meg!) Az érdeklődőknek tudom küldeni.
|
| Előzmény: [72] Hajba Károly, 2003-11-14 08:40:05 |
|
| [72] Hajba Károly | 2003-11-14 08:40:05 |
 Kedves Zoli!
Isten hozott a kockabűvöltek táborába!
Beszkennelem a cikket, de feltételezem, hogy a Fizikai Szemlebeli cikk részletesebb lehet. Ti. késöbb jelent meg és többen jegyezték.
> Ti láttatok már 4*4*4 Rubik-kockát?
Anno volt a kezemben egy, talán kölcsön is kaptam egy hétre, de lehet, hogy az a dodekaéder volt. Ki tudja, ezirányú emlékeimet belepte már a rozsda. Tény, hogy nem bírtam vele :o(
Üdv: Károly
|
| Előzmény: [71] SchZol, 2003-11-14 05:48:40 |
|
| [71] SchZol | 2003-11-14 05:48:40 |
 Kedves Károly!
Engem érdekelne a Rubik-kockás cikk, ha beszkenneled. Nagyon szeretem a Rubik-kockát, hetente egy párszor mindig kirakom. Ti láttatok már 4*4*4 Rubik-kockát? Sajnos Én még nem láttam, csak hallottam róla.
Üdv, Zoli
|
|
| [70] Hajba Károly | 2003-11-13 23:50:18 |
 Kedves László!
Nem azt a cikket ismerem, hanem a könyvbelit (A bűvös kocka - Gondolat - 1981), amit még csak Marx jegyzett (no nem a Tőkés :o).
A 'spin' pedig, hát... anno szerettem a fizika ezen részét is.
Ha érdekel a könyvbeli cikk, megpróbálhatom beszkennelni és drótpostán elküldeni.
Üdv: Hajba Károly
|
| Előzmény: [68] lorantfy, 2003-11-13 23:16:47 |
|
| [69] lorantfy | 2003-11-13 23:22:51 |
 Az 5. feladatra: még nem írtunk megoldást. Az eredeti szöveg: Adott 100 láda mindegyikben 1000 db 2 grammos 1 forintos, kivéve egyet amiben 1 grammosak az 1 forintosok. Legkevesebb hány mérésből tudjuk eldönteni melyik ládában vannak a selejtes egy forintosok, ha minden láda ugyanúgy néz ki, és csak egy egykarú mérlegünk van.
Aki nem ismeri annak érdemes átgondolni a trükköt: Sorszámozzuk meg a ládákat 1-100-ig és minden ládából tegyünk fel a mérlegre annyi forintost amennyi a láda sorszáma. Ezt mérjük le. Ha minden ládában 2 grammos érmék lennének akkor (1+100)x100 = 10100 grammot kellene mérnünk. Amennyivel kevesebbet mérünk annyi a keresett láda sorszáma.Tehát egy mérés elegendő.
Az eredeti kitűző – Sch Zoli – nehezítése:
15. feladat: Hány mérés szükséges, ha a 100 közül két ládában vannak 1 grammos forintok.
|
| Előzmény: [6] SchZol, 2003-11-01 22:12:06 |
|
| [68] lorantfy | 2003-11-13 23:16:47 |
 Kedves Lajos!
Örülök, hogy feltetted a megoldást. Úgy néz ki a „fiatalok” tényleg nem harapnak erre a témára. A „spin” szóhasználatból arra következtetek, hogy talán Te is olvastad a Fizikai Szemlében megjelent cikket (21 éve) Ha esetleg valakinek meglenne elektronikus formában köszönettel venném:
MARX GY., GAJZÁGÓ É., GNÄDIG P., ZÁMBÓ V.: A bűvös kocka univerzuma - Fizikai Szemle 32 (1982) 73-77
|
| Előzmény: [59] Hajba Károly, 2003-11-13 00:09:23 |
|
|
|
| [65] Lóczi Lajos | 2003-11-13 18:57:33 |
 Álljon itt a háromszöges feladat egy általánosítása: az alapon fekvő szögek a 80o helyett legyenek  , a 60o-os BAE szög helyett legyen , a 60o-os BAE szög helyett legyen  , a 70o-os ABD szög pedig legyen most , a 70o-os ABD szög pedig legyen most  ; ezekről tehát azt tesszük fel csak, hogy 0< ; ezekről tehát azt tesszük fel csak, hogy 0< <90o, 0< <90o, 0< < < , 0< , 0< < < . Jelölje továbbá a keresett BDE szöget . Jelölje továbbá a keresett BDE szöget  . A rövidség kedvéért egy x szög tangensét jelölje . A rövidség kedvéért egy x szög tangensét jelölje  x. x.
Ekkor elemi koordinátageometriai érvelés mutatja, hogy
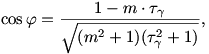
ahol 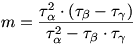 . .
Az  =80o, =80o,  =60o, =60o,  =70o értékeket behelyettesítve, "némi" algebrai egyszerűsítés után például az alábbi alakot kapjuk (ki-ki maga is megpróbálkozhat eljutni idáig): =70o értékeket behelyettesítve, "némi" algebrai egyszerűsítés után például az alábbi alakot kapjuk (ki-ki maga is megpróbálkozhat eljutni idáig):
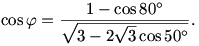
13. feladat. Bizonyítsuk be, hogy a fenti kifejezés jobb oldala cos 20o.
|
| Előzmény: [63] Kós Géza, 2003-11-13 14:25:51 |
|
| [64] jenei.attila | 2003-11-13 17:28:42 |
 Ötletes a hivatkozott KÖMAL-ban közölt 18 szöges megoldás, bár abban a feladatban az ABD szög 50 fok. Valószínűleg a módszer alkalmazható akkor is, mikor ABD szög=70 fok. Kiváncsi lennék a 18 szöges megoldástól független megoldásra ABD=50 fok esetén.
|
| Előzmény: [63] Kós Géza, 2003-11-13 14:25:51 |
|
|
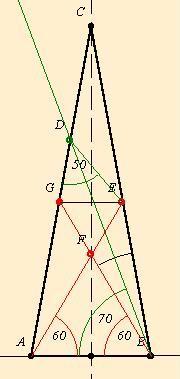
| [62] lorantfy | 2003-11-13 13:51:17 |
 Kedves Csillag és Attila!
Szép a megoldás! Egy ábrát megérdemel.
|
 |
|
| [61] jenei.attila | 2003-11-13 10:34:03 |
 Szia Csillag!
Szép megoldás, gratulálok. Egy két apróbb megjegyzést tennék. Amikor felírtad, hogy GD=GF=GE, innen már azonnal következik, hogy GDE szög = GED szög = 50 fok, de ADB szög = 30 fok, amiből EDB szög = 20 fok. Csak egy kis egyszerűsítés. Az én megoldásom is hasonló, megtartva a Te jelöléseidet, a következő: DC/GD=CB/CE=AB/GE. A GE félegyenesen vegyük fel H pontot úgy, hogy GH=GC legyen. Ekkor EH=GH-GE=GB-GF=FB=AB. Vagyis DC/GD=AB/GE=EH/GE miatt CH párhuzamos DE-vel. De GCH szög=GHC szög= 50 fok (mivel GC=GH) =GDE szög. EDB szög=GDE szög -ADB szög= 50-30=20 fok. A TeX-hel még nem tudok rendesen bánni, legközelebb azért megpróbálom.
|
| Előzmény: [57] Csillag, 2003-11-12 22:20:02 |
|
| [60] Hajba Károly | 2003-11-13 00:31:47 |
 Ha (46) Jenei Attila geometriai feladata a 10. és (52) Bubu kérdése a 11. akkor
12. feladat: Kössük össze 12 darab, folytonos, a kiinduló pontba visszazáródó és a külső pontsoron túl nem nyúló egyenes szakasszal (azaz egy 12 szakaszból álló hurokkal) az alábbi 49 pontot.
HK
|
 |
|
| [59] Hajba Károly | 2003-11-13 00:09:23 |
 Kedves László!
Úgy tűnik nekem, hogy csak ketten vagyunk jelen abból a generációból, kiket elbűvölt a bűvös kocka, habár jelenleg is kapható. Ezért is ill., hogy Mihály kérésére csökkenjen a megoldatlan feladatok száma, válaszolok a bűvös kockás feladatra.
Megoldás a 9. feladatra:
Az eredeti kockán található oldaléleknek két állásuk lehetséges, alaphelyzet ill. (180°-os) elforgatottság. Nevezzük 0 ill. 1/2 spinnek. Egy rendesen összeállított kocka spinjei mindig egész számot adnak ki, tehát első ránézésre a bűvös hasáb rendellenesen lett összeállítva, ami persze nem igaz, mivel alaphelyzetből és 0 spinnel lett összekeverve.
Ha jobban megnézzük az ábrát, látható, hogy a hasáb forma miatt 4 oldalél "le lett vágva", így azoknak csak egy színűk van, de ha 180°-kal elforgatom, önmagába tér vissza. Így e 4 elemnél a 0 és 1/2 spin teljesen egyformának tűnik. Ha az összekeverés előtt egy aszimetrikus jellel meg lettek volna jelölve, akkor 1 vagy 3 elem 1/2 spin elfordulást mutatna.
Hajba Károly
|
| Előzmény: [43] lorantfy, 2003-11-08 15:50:59 |
|
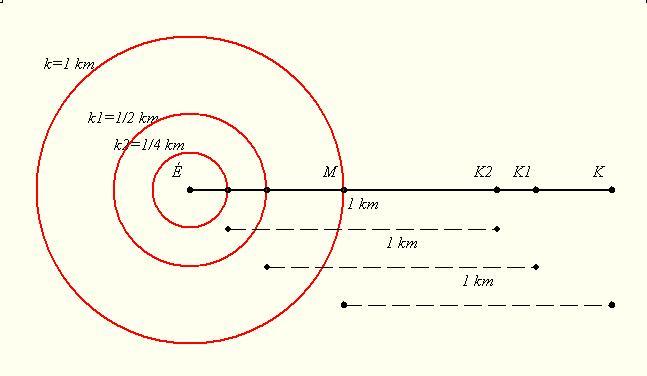
| [58] lorantfy | 2003-11-12 22:31:25 |
 Kedves Lajos!
Nekem az 1 km helybenjárás kelet felé az nem tetszik, de miközben gondolatban ráhúztál a határesetre megálltál-e n-szer az 1/n sugarú köröknél és beidomítottad-e a medvét, hogy menjen körve n-szer kelet felé? Mert ha igen tiéd a Nagy Polarbear emlékérem. Persze mindig kicsit közelebbről kell elindítani a medvét. ( A felülnézeti ábrán a távolságok nem arányosak!)
Sirpinek gratula a jó ötletért!
|
 |
|
| [57] Csillag | 2003-11-12 22:20:02 |
 Üdv Mindenkinek!
Sajnos ábrát nem tudok rajzolni, de egy megoldást elmondok a geometria példához: E tükörképe a C-nél levő szögfelezőre G. A C-nél levő szögfelező és az AE metszéspontja F. GD=GF, mert
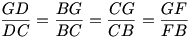
(szögfelezőtétel többszöri felhasználása, GCB =GBC =GBC =20o) =20o)
Tehát GD=GF=GE=FE(mert GEF szabályos háromszög). BGA =40,FGD =40,FGD =140,GDF =140,GDF =20,DF||CB,FDB =20,DF||CB,FDB =DBC =DBC =10,DGE =10,DGE =80,GDE =80,GDE =50,BDE =50,BDE =GDE =GDE -GDF -GDF -FDB -FDB =20. =20.
Vagyis a keresett szög 20 fokos.
GB
|
| Előzmény: [46] jenei.attila, 2003-11-10 10:44:46 |
|
| [56] Lóczi Lajos | 2003-11-12 19:38:44 |
 Tetszetős ez a megoldás... Kérdezném, kinek mi a véleménye e megoldás alábbi határesetéről: az északi sarkponttól 1 km-re délfelé kezdi meg az útját; 1 km-t északra haladva bejut az É sarkra, kelet felé onnan nem tud (mert nem lehet) haladni, tehát nem mozdul, majd dél felé 1 km-t ballag és visszajut a kezdőpontba.
Azaz, elfogadjuk-e "1 km keletre haladásnak" azt, ha valahol nem lehet kelet felé haladni.
Másik megjegyzésem: hogyan lehetne (formálisan, esetleg rajz nélkül) bizonyítani, hogy több lehetséges útvonal nincsen? (Hiszen az első megoldás is meggyőzőnek tűnt.)
Azzal is érdekes -- és minden bizonnyal sokmegoldású -- feladatokat lehetne gyártani, ha pl. a megtett távolságok összemérhetők/meghaladják a bolygó (fél)kerületét.
|
| Előzmény: [55] Sirpi, 2003-11-12 14:58:22 |
|
| [55] Sirpi | 2003-11-12 14:58:22 |
 Lorybetti: a feltételek csak úgy teljesülhetnek, ha a medve kezdetben pontosan a déli sarkponton áll, majd halad É fele, K fele és D fele és visszajut a déli sarkpontra.
Nem csak így lehet... Vegyünk az északi sarkpont közelében egy olyan szélességi kört, aminek kerülete osztja az 1km-t, és a kiindulópont ettől 1km-rel délre legyen. Ebben az esetben az É, K, D út triviálisan a kezdőpontba vezet, és akkor mégse pingvint találtunk :-) Vagyis az eredeti feladat is értelmes, nem kell permutálni az irányokat.
S
|
| Előzmény: [50] lorybetti, 2003-11-10 22:23:48 |
|
|
|
| [52] Bubu | 2003-11-12 01:14:45 |
 Rendbonto leszek, elnezest erte... Szoval a billiardgolyos feladat (amit egyebkent anno GY peldakent lekuzdottem:)) egy kulonleges matematikai kepzettseggel nem biro (erettsegi), de egyebkent feletteb intelligens rokonomat "megihlette". Azt allitja, hogy 5 meressel 12 golyobol ki tud valasztani 2 db eltero tomegut! Precizebben: van 12 kulsore egyforma golyo. 10 tomege megegyezik, kettoje elter (hogy milyen "iranyban" es mennyire, azt nem tudjuk). Egy ketkaru merleg segitsegevel valasszuk ki a ket kulonc golyot ot meressel. A megoldasrol sejtelmem sincs, de a hetvegen fogok vele foglalkozni. Aki barmilyen reszeredmenyt/otletet tud, az mailezzen legyen szives!
|
|
| [51] lorantfy | 2003-11-11 23:00:51 |
 A tevés feladat megoldása:
Az osztószámok: k , l, m, a tevék száma: n és k < l < m < n.
A végakarat teljesítésének szükséges feltétele a kölcsönkért 1 tevével:
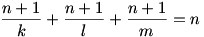
Mindkét oldalt elosztva (n+1) –el és 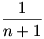 –et mindkét oldalhoz hozzáadva: –et mindkét oldalhoz hozzáadva:
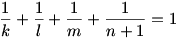
Ezt az egyenletet kell megoldanunk a 0 < k < l < m < n+1 : egész számok feltétellel.
Látszik, hogy k = 2, ugyanis k = 3 esetén a lehető legkisebb l, m, n+1 értékekre is az összeg 1-nél kisebb:
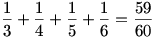
Már csak három ismeretlenünk van:
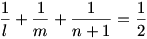
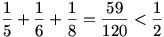
emiatt l lehetséges értékei: l = 3, l = 4
Kezdjük l = 3–mal:
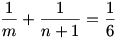
és 6 < m < 12 ( az összeg felének reciprokánál kisebb)
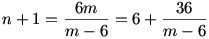
Tehát (m-6) osztója 36-nak.
m = 7, n+1 = 42, n = 41 jó megoldás,
m = 8, n+1 = 24, n = 23 jó megoldás,
m = 9, n+1 = 18, n = 17 jó megoldás,
m = 10, n+1 = 15, n = 14 NEM jó megoldás, mert 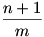 nem egész szám. nem egész szám.
l = 4 a következő eset
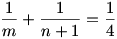
és 4 < m < 8 ( az összeg felének reciprokánál kisebb)
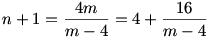
Tehát (m-4) osztója 16-nak.
m = 5, n+1 = 20, n = 19 jó megoldás,
m = 6, n+1 = 12, n = 11 jó megoldás.
Összesen 5 megoldást találtunk!
|
|
| [50] lorybetti | 2003-11-10 22:23:48 |
 Kedves Fálesz Mihály!
Egyetértek Veled, így szeretném csökkenteni a megoldatlan példák számát.A medvés példa- Fizban 22.es hozzászólása A szöveg így szólt: "Elindul Észak felé, és megy 1 km-t. Ezután elfordul Kelet felé, és megint megtesz 1 km-t. Aztán Délnek fordul, és -ki gondolta volna- megtesz még 1 km utat. Ezután a medve visszajut a P pontba."
A feladat megoldása: a feltételek csak úgy teljesülhetnek, ha a medve kezdetben pontosan a déli sarkponton áll, majd halad É fele, K fele és D fele és visszajut a déli sarkpontra. Tartok töle, hogy Fizban rosszul írta az irányokat, mert így a medve fekete-fehér színű és Pingvin névre hallgat. Ha jegesmedvéről lenne szó-ami persze fehér: az irányok sorrendje: D, K és É vagy K, É, D vagy É, D, K (utóbbi két esetben csak érinti az északi sarkpontot)
Értékes megjegyzés: A medve olyan gömbi háromszögben mozog, melynek minden szöge derékszög. Lehet hogy Bolyait is ez ihlette meg?
|
|
| [49] Fálesz Mihály | 2003-11-10 18:10:51 |
 Sziasztok,
Kicsit kezdenek elburjánzani a meg nem oldott feladatok. Pillanatynilag a következőkre nincs még teljes megoldás:
-- 2. feladat (9 pont), 2. hozzászólás
-- 3. feladat (emberevők) [3]
-- 5. feladat (100 láda pénz) [6]
-- milyen színű a medve [22]
-- tevék [26]
-- Rubik-hasáb [43]
-- mekkora az EDB szög [46-47]
Összesen 7, ami túl sok. Azt javaslom, hogy most egy darabig ne írjunk új feladatokat, inkább ezekere lássunk megoldást, és a továbbiakban is törekedjünk arra, hogy ne legyen egyszerre - mondjuk - háromnál több megoldatlan feladat.
F.M.
|
|
| [48] Sirpi | 2003-11-10 14:18:59 |
 Ez a szummafelcserélés tökéletes megoldás, gratula, én is így csináltam (mellesleg azért nem így adtam fel, mert így sokkal könnyebb, csupán a 2, 3, 5, 8 kitevőket kivéve szerintem nehezebb feladatot kapunk.
|
| Előzmény: [40] Pach Péter Pál, 2003-11-07 23:14:59 |
|
| [47] lorantfy | 2003-11-10 11:21:06 |
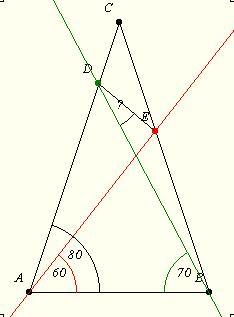
 Egy ábra a lenti feladathoz. (Imádom az Euklides programot!)
|
 |
|
| [46] jenei.attila | 2003-11-10 10:44:46 |
 Egy geometria feladat: Az ABC egyenlő szárú háromszög AB alapon fekvő szögei 80 fokosak. A-ból az alappal 60 fokos szöget bezáró egyenes a BC szárat E pontban, B-ből az alappal 70 fokos szöget bezáró egyenes az AC szárat D pontban metszi. Mekkora az EDB szög?
|
|
| [45] Hajba Károly | 2003-11-10 01:19:09 |
 > köszönöm, hogy ilyen szép táblázatos formában feltetted az eredményt
Tanulom a TeX-et. :o)
> Te biztosan emlékszel még a RUBIK kockára
Mi az, hogy emlékszem! Engem a gimi 3. osztályában ért (ma 11. o.), s a kockám nemegyszer a tanári asztalon vészelte át az óra második felét több más kockával egyetemben. Így az ábrád öt percnyi tanulmányozása után rájöttem a "trükk"-re, de hagyok mást is gondolkodni.
|
| Előzmény: [43] lorantfy, 2003-11-08 15:50:59 |
|
| [44] Lóczi Lajos | 2003-11-09 16:21:43 |
 Valóban, ez így szép és jó. Utólag természetesen a "mi" formulánkat is megtaláltam, pl. a http://mathworld.wolfram.com/RiemannZetaFunction.html oldalon ez a (23)-as formula :-) Érdemes megnézni, van néhány szép ábra (és csaknem 100 egyéb dzeta-képlet)...
|
| Előzmény: [40] Pach Péter Pál, 2003-11-07 23:14:59 |
|
| [43] lorantfy | 2003-11-08 15:50:59 |
 Kedves Károly!
Gratulálok a megoldáshoz és köszönöm, hogy ilyen szép táblázatos formában feltetted az eredményt!
Te biztosan emlékszel még a RUBIK kockára és remélem, hogy a fiatalabbak is ismerik. Nekem nagy sikerélmény volt, hogy meg tudtam oldani. 3 napom ment rá egy téli vizsgaidőszakban és meg is lett az eredménye, 4-es lett az analízis vizsgám… A következő nyáron Angliában jártam és ott lehetett kapni a Rubik kocka mindenféle változatát. Vettem is egy nyolcszög alapú hasáb alakút és összekeverés után a begyakorolt transzformációkkal próbáltam visszaforgatni az alaphelyzetbe. Rejtélyes módon az alábbi eredményre jutottam: egy élközépen lébő kocka megfordult a többi mind a helyére került. 9. feladat : Hogyan lehetséges ez?
|
 |
|
|
| [41] lorantfy | 2003-11-08 00:39:03 |
 Kedves Fórumosok !
Örülök, hogy ilyen sokan foglalkoztatok a biliárdgolyós példával, még idemásolok egy megoldást, ami felhasználja ugyan az előbbi mérés eredményét, de talán annak aki később idetéved érthetőbb:
A 12 golyót 3 4-es csoportra bontom.
OOOO OOOO OOOO
Két 4-es csoportot összehasonlítok a mérleggel (1. mérés)
OOOO -- OOOO
1.1. Egyenlők: ekkor a maradék 4 között van az eltérő
OOOO = OOOO HHHH
Veszek 2-t az első 8 golyó közül (ezek jók) és 2-t a maradék 4-ből
OO -- HH HH
Összemérem őket (2. mérés),
1.2. Ha lebillen a mérleg akkor a mérlegen lévő kettő (HH) közül a 3. méréssel eldöntöm melyik az eltérő golyó.
1.3. Ha egyenlő a 2. mérés eredménye akkor a nem mért 2 közül (HH) döntök a 3. méréssel. (Egyiket összemérem egy jó golyóval)
2.1. Ha a két 4-es csoport összemérésekor lebillen a mérleg. Ekkor amerre lebillent azt a 4 golyót N betűvel jelölöm ( ezek között lehet egy nehezebb)a másik oldalon lévő 4-et K betűvel jelölöm (ezek között lehet egy könnyebb)
Pl.: KKKK < NNNN OOOO
2.2. Bal oldalra felteszek a mérlegre 3 db K jelű golyót és 1 db N jelűt, jobb oldalra pedig 1 db (a megmaradt) K jelűt és a 3 db biztosan jó golyót. (Még 3 db N jelű és egy jó (O) marad ki)
KKKN -- KOOO NNN O
Nézzük az eseteket:
3.1. Ha a mérleg jobbra billen le. Ekkor a bal oldali 3 K közül 1 golyó könnyebb.
KKKN < KOOO NNN O
Ezek közül egy méréssel tudok dönteni, hiszen tudom, hogy a hibás golyó könnyebb. Kettőt összemérek, amelyik felemelkedik az a hibás. Ha egyenlő a kettő összemért, akkor a 3. a hibás golyó.
3.2. Ha a mérleg egyensúlyban marad akkor a kimaradt 3 db N jelű golyó
KKKN = KOOO NNN O
között van egy nehezebb, amit a 3. méréssel az előzőhöz hasonlóan el lehet dönteni.
3.3. Ha a mérleg balra billen ki, akkor ezt okozhatja a bal oldali N jelű golyó vagy a jobb oldalon lévő K jelű golyó.
KKKN > KOOO NNN O
Ezt a 3. méréssel könnyen el lehet dönteni, ha pl. a K jelűt összemérem egy jó golyóval. Ha felemelkedik akkor ez a hibás, ha egyenlők, akkor az N jelű.
|
|
| [40] Pach Péter Pál | 2003-11-07 23:14:59 |
 A 8. feladatra írok megoldást, úgyhogy, aki még nem oldotta meg (és szeretne rajta gondolkozni), ne olvassa tovább. Tekintsük a következő átalakításokat:
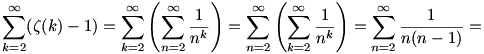
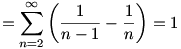
Pozitív számokat összegzünk, és a határérték valóban létezik (olvassuk az átalakításokat hátulról visszafelé), így nem "csaltunk", amikor megcseréltük a két szummát. Ezen kívül a mértani sor összegképletét, és egy ún. "teleszkópos trükköt" alkalmaztunk.
Az előbb bizonyított állítás nyilvánvaló következménye, hogy
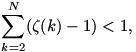
ugyanis az előbbi összegnek van olyan tagja, ami ebben az összegzésben nem szerepel. (Mint már megállapítottuk, minden tag pozitív: 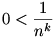 ) )
Pach Péter Pál
|
| Előzmény: [30] Lóczi Lajos, 2003-11-05 23:59:16 |
|
| [39] lorantfy | 2003-11-07 09:56:01 |
 A biliárdgolyós példa alábbi megoldását Gáti Beatrix küldte nekem.
|
 |
|
| [38] lorantfy | 2003-11-06 23:19:20 |
 Kedves Csillag! Nagyon szép a megoldásod, gratulálok! Holnap felteszek hozzá egy táblázatot, hogy mikor melyik golyó jön ki, igy mindenki ellenőrizheti, hogy jó is. Elemben a tevés példán gondolkodók még keresgélhetnek, ha van idejük, mert én 5 megoldást találtam.
|
|
| [37] Csillag | 2003-11-06 16:02:59 |
 A billiárdgolyós probléma mindkét nehezített változatát megoldja a következő három mérés. Ezzel 12 golyó esetén meghatározható, hogy melyik volt hibás és hogyan, 13 golyó esetén pedig, hogy melyik volt hibás: 1.mérés: (x1,x2,x3,x4) összehasonlítása (x5,x6,x7,x8)-cal 2.mérés: (x1,x2,x5,x11) összehasonlítása (x3,x6,x9,x10)-zel 3.mérés: (x1,x6,x9,x11) összehasonlítása (x3,x4,x7,x12)-vel
|
| Előzmény: [20] Kós Géza, 2003-11-05 12:21:41 |
|
| [36] Kós Géza | 2003-11-06 14:24:35 |
 Kedves Csimby,
Amit írtatok, az mindenképpen megérdemel egy fél Túró Rudit, de jobb lenne egy szép, világos, kerek megoldássá átírni. Ehhez pontosabban kell kezelni a falvak és a hittérítők lehetséges állapotait.
|
| Előzmény: [23] Csimby, 2003-11-05 18:21:35 |
|
| [35] lorantfy | 2003-11-06 14:18:01 |
 Az eredeti tevés példa úgy szólt, hogy 11 tevét örökölnek és hogyan oszthatnák el ha a legidősebb felét, a középső harmadát, a legkisebb hatodát örökölte. És a bölcs kádi javaslatára kölcsönkérnek egy tevét, amit az osztozkodás után vissza is adnak.
|
|
|
|
| [32] Hajba Károly | 2003-11-06 12:31:28 |
 A 7. feladathoz:
Először is elnézést mindenkitől, de még nem sikerült elmélyedni a TeX-ben, így annak lehetőségeit most nem használom ki. (De ami késik, nem múlik.)
Mivel a tevék számához még 1-t hozzáadva el tudták osztani kényelmesen és még meg is maradt a kölcsönteve, ezért a K, L, M számok reciprokösszege alulról közelíti az 1-t, de nagyobb mint a legkisebb elérhető N-re N/(N+1)=0,9; ahol N=2+3+4=9. (Lehet ennél finomabban is lehatárolni.)
Tehát azokat a számhármasokat kell megvizsgálni, melyek reciprokösszege ebbe a tartományba esik. K=2, mivel a 3, 4, 5 számhármasra 0,78..; továbbá 2, 4, 5 számhármasra 0,8666... jön ki, mint alsó korlát, másrészről 2, 3, 6 számhármasra 1,00 jön ki, mint felső korlát. Én a két számhármas között két megoldást találtam:
K=2, L=3, M=7, N=41
K=2, L=4, M=6, N=11
Hajba Károly
|
| Előzmény: [26] lorantfy, 2003-11-05 21:34:18 |
|
| [31] Rizsa | 2003-11-06 12:27:26 |
 A tevel szama 17, es 2, 3, 6 reszre kell bontani a majdani 18at.
|
|
| [30] Lóczi Lajos | 2003-11-05 23:59:16 |
 Mivel közben sikerült tisztáznom az előző hozzászólásban megfogalmazott sejtésem (a bizonyítás nem nehéz, teljesen elemi, csak két apró ötlet kell, és minden szükséges információ megtalálható a hozzászólásban), ezért
8. feladat: Mutassuk meg, hogy tetszőleges N 2 természetes számra 2 természetes számra
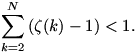
|
| Előzmény: [29] Lóczi Lajos, 2003-11-05 23:20:59 |
|
| [29] Lóczi Lajos | 2003-11-05 23:20:59 |
 Az 1. feladattal kapcsolatban a következő érdekes általánosítás tűnik igaznak: nevezetesen nem számít, hogy mely hatványfüggvények reciprokait szerepeltetjük a szummákban (ami ott 2, 3, 5, illetve 8 volt). A rövidség kedvéért vezessük be a következő (szokásos) jelölést: ha s>1 valós szám, akkor legyen
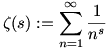
a híres-nevezetes dzeta-függvény. (Mint ismeretes, ennek a függvénynek komplex s-ekre történő kiterjesztése szerepel az egyik leghíresebb, mindmáig megoldatlan matematikai sejtésben, a Riemann-hipotézisben.)
Ezzel a jelöléssel az előző hozzászólásban beláttuk tehát, hogy
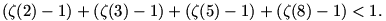
Sejtésem a következő: 2-től kezdve akárhány ilyen tagot adunk össze, az összeg mindig kisebb lesz 1-nél, azaz, ha N 2 tetszőleges természetes szám, akkor 2 tetszőleges természetes szám, akkor
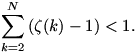
A sejtést alátámasztják a Mathematica programmal végzett numerikus kísérletek (például ha N=50, akkor a fenti összeg körülbelül 0,99999999999999911...), valamint a Mathematica azon állítása, hogy
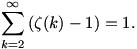
(Ha a program ezt állítja, akkor valószínűleg ezt már bebizonyította valaki, a sejtéshez nyilván "elég" lenne ez utóbbi állítást megmutatni, hiszen a szumma N-ben monoton nő.)
A sejtéssel kapcsolatos bármely észrevételt szívesen veszek.
|
|
| [28] Lóczi Lajos | 2003-11-05 22:56:02 |
 Ha szabad integrálokat használni, akkor következzen egy megoldás az 1. feladatra.
Mivel az összegzendő kifejezések szigorúan monoton fogyóak, ezért felfoghatók integrálok alsó (téglalapos) közelítőösszegeiként -- csak arra kell vigyáznunk, hogy az integrálás határát 1-gyel hamarabb kezdjük, mint a szummázásét. (A szumma első két tagját külön kell kezelnünk, mert különben felső becslésünk túl durva lenne.) Tehát
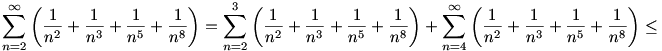
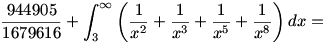
![\frac{944905}{1679616}+\left[-\frac{1}{x}-\frac{1}{2x^2}
-\frac{1}{4x^4}-\frac{1}{7x^7} \right]_3^\infty=
\frac{944905}{1679616}+\left( 0+\frac{24007}{61236}\right)=](keplet.cgi?k=FE7C5468F3C5143E)
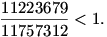
|
| Előzmény: [1] Sirpi, 2003-10-30 10:07:33 |
|
| [27] Lóczi Lajos | 2003-11-05 22:15:39 |
 A már említetteken kívül pár egyéb "ötlet" a tréfás kérdés megválaszolásához.
Az ex függvényen kívül a (konstans.ex) függvény, mint általános megoldás is szóba jöhet (abban az értelemben, hogy a függvény és deriváltja megegyezik).
Speciálisan a kuncogó függvény lehet az azonosan nulla függvény is.
De kuncoghat azért is, mert ő mondjuk a Dirichlet-függvény (amely tehát racionális pontokban 1, irracionálisokban 0, s így sehol sem folytonos, sehol sem deriválható).
Sőt, kuncoghat azért is, mert ő pl. az x2 függvény, s így deriválás után az értékkészlete nagyobb lesz.
|
| Előzmény: [11] enel, 2003-11-04 14:32:31 |
|
| [26] lorantfy | 2003-11-05 21:34:18 |
 Valamikor régen amikor a Scientific American még Tudomány néven magyarul is megjelent olvastam benne egy matek feladványt. De sajnos ez olyan régen volt, hogy a pontos számokat már elfelejtettem, így kénytelen vagyok a feladatot általánosan megfogalmazni: 7. feladat: A gazdag tevekereskedő mielőtt meghalt magához hívta 3 fiát és elmondta nekik, hogy rájuk hagyja N db tevéjét. A tevék K-ad részét a legidősebb, L-ed részét a középső és M-ed részét pedig a legkisebb fia kapja. A kereskedő halála után a fiúk bajban voltak mert az N szám K, L, M egyikével sem volt osztható. Szerencsére éppen egy tevekaraván haladt át a falun és a legkisebb fiúnak támadt egy ötlete. Kölcsönkért egy tevét a karavánból. Így az N+1 tevét el tudták osztani egymás között a végakaratnak megfelelően és még maradt is 1 teve, amit visszaadtak a tulajdonosának. Milyen K,L,M,N számokra teljesíthető a fenti felosztás ? ( K<L<M<N pozitív egész számok!)
|
|
| [25] Kritya3 | 2003-11-05 20:47:52 |
 Most egy kicsit offolok, remélem nem orrol meg rám a Moderátor: olyat hallottam, hogy OKTV napján a versenyig még egy számot sem szabad összeadni.
|
| Előzmény: [21] Frenky, 2003-11-05 15:56:04 |
|
| [24] Rácz Béla | 2003-11-05 19:04:54 |
 Ha valakit szétvetne a kíváncsiság, közölhetem, hogy az összes eddigi kétkarú mérleges feladat megtalálható a Skljarszkij-Csencov-Jaglom: Válogatott feladatok és tételek az elemi matematika köréből c. gyűjteményben (I. kötet, rögtön az eleje.)
Igazából ezt a könyvajánlóba kellett volna írnom, mert a Skljarszikij messze a legjobb matekkönyv, ami valaha is a kezembe került. Szovjet minőség!!! ;-)
|
| Előzmény: [20] Kós Géza, 2003-11-05 12:21:41 |
|
| [23] Csimby | 2003-11-05 18:21:35 |
 MEGOLDÁS A SZIGETES FELADATHOZ:
Akkor esznek meg egy papot amikor a legközelebbi olyan faluba ér ahonnan egy társa indult (ha egyedül van akkor amikor az indulási faluba visszaér). Tehát ha kezdetben P pap indult, amikorra mindet megeszik, P falu lesz pogány méghozzá az a P amelyből indultak (hiszen egészen addig nyugodtan téríthet egy pap amíg indulási helyre nem ér, ahol is hívő falut talál: -> megeszik, az indulási falu pogány lesz. -> az addig útbaeső falvakat megtéríti*. Az utánuk indulók, mivel nem indulhatnak a meglévő pogány falukból (hiszen ezek induló faluk voltak és mindenki más faluból indul) biztosan olyan faluból kell, hogy induljanak amelyeket már megtérítettek, tehát amint elindulnak, rögtön megeszik őket. Mindenki máshonnan indul, tehát mindenkit máshol esznek meg, tehát mindegyik falu pogány lesz. * probléma akkor lehet, ha a P db pap indulása után még indulnak valamikor pap(ok), de ez még az előtt történik, hogy kialakulna az a helyzet amikor már csak a P db indulási falu pogány (azaz amikor még lehet olyan helyekről indulni amelyet még senki sem térített meg). Ekkor két eset lehet: - az induló már megtérített faluból indul -> meghal rögtön, és a falu pogány lesz - pogány faluból indul (amelyben előtte még senki sem járt) , ekkor felfoghatjuk úgy mintha P+1 pap indult volna, és ugyanaz a megoldás mint P-re.
Kiss Gábor és Csajbók Bence
|
|
| [22] Fizban | 2003-11-05 17:53:20 |
 Üdv mindenkinek!
Az én feladatomat biztosan sokan ismerik, de azért leírom, hátha valakinek új:
Van egy medve a Földön egy P pontban. Elindul Észak felé, és megy 1 km-t. Ezután elfordul Kelet felé, és megint megtesz 1 km-t. Aztán Délnek fordul, és -ki gondolta volna- megtesz még 1 km utat. Ezután a medve visszajut a P pontba. A kérdés: Milyen színű a medve?
|
|
| [21] Frenky | 2003-11-05 15:56:04 |
 Üdv! nos igen szóval addig eljutottam hogy csoportok kellenek aztán elkezdtem nézni hogy mlyen csoportok néztem 2 erre rájöttem hamar hogy rossz néztem a 3-at ezzel sokat szenvedtem meg persze a 4gyel és ezzel is jutottam elgtovább valahogy úgy próbáltam hogy a régebbi mérés golyóit is belevonoma dologba , pl a régi mérésből két golyót kicserélek a bizonytalan golyók valamelyikére , és akkor ugye ha megint eldől a serpenyő akkor még mindig köztük van a gyanús ha meg nem dől el akkor azok közül az egyik amit elvettem , de végül mindig úgy lett hogy van két gyanús golyóm és nincs több mérés...vagy estetleg 3 bizonytalan golyó és egy mérés.
holnap matek OKTV:-) úgyhogy holnap délelőtt lesz időm letisztázni és föladni a kömalt:-) hozzá is kezdek még most(annál többet alhatok)
|
|
| [20] Kós Géza | 2003-11-05 12:21:41 |
 Az feladatot én eredetileg úgy ismertem, hogy azt is meg kell mondani, hogy a kakukktojás könnyebb vagy nehezebb a többinél. Ez ugyan nehezítés, de segít abban, hogy az első mérést kitaláljuk.
Ha n mérésünk van hátra, akkor azoknak összesen 3n lehetséges kimenetele lehet, ezért legfeljebb ennyi lehetséges esetet tudunk a mérések által megkülönböztetni. (Ez akkor is igaz, ha az egyes mérések összeállítása függ a korábbi mérések eredményétől.)
Kezdetben 24 eset van, mert 12 golyó lehet a kakukktojás, és a kakukktojás könnyű és nehéz is lehet. A 3 mérés legfeljebb 33=27 esetet különböztethet meg, a becslés itt (még) stimmel.
Az első mérésnél ugyanannyi golyót, mondjuk k darabot kell tennünk a két serpenyőbe. Az első kérdés, hogy mennyi legyen a k.
Ha a mérleg egyensúlyban marad, akkor a többi 12-2k golyó között van a kakkukktojás, ami összesen 2(12-2k) esetet jelent. Ha k 3, akkor ez legalább 12 eset, amit nem lehet 2 mérésből megkülönböztetni. Ha k 3, akkor ez legalább 12 eset, amit nem lehet 2 mérésből megkülönböztetni. Ha k 4, akkor legfeljebb 8 eset. A k-t tehát nem szabad 4-nél kisebbnek választanunk. 4, akkor legfeljebb 8 eset. A k-t tehát nem szabad 4-nél kisebbnek választanunk.
Ha a mérleg nincs egyensúlyban, akkor 2k ,,gyanús'' golyónk van. Ebből k darab ,,nehéz-gyanús'', a másik k darab pedig ,,könnyű-gyanús'', ez összesen 2k eset. A hátralevő két mérés legfeljebb 9 esetet különböztethet meg, tehát k-t nem szabad 4-nél nagyobbnak választani.
Összefoglalva, az első mérésnél csak négy-négy golyót tehetünk a két mérlegserpenyőbe. Már csak a további méréseket kell kitalálni. :-)
* * *
Aki ismeri vagy már megoldotta a feladatot, gondolkodhat két változaton.
Első változat: van 13, látszólag egyforma golyó, az egyik könnyebb vagy nehezebb a többinél. Három mérésből mondjuk meg, melyik az. (Nem kell megmondani, hogy könnyebb, vagy nehezebb.)
Második változat: van 12, látszólag egyforma golyó, az egyik könnyebb vagy nehezebb a többinél. Három mérésből mondjuk meg, melyik az, és azt is, hogy könnyebb, vagy nehezebb. (Eddig ugyanaz a feladat.) A nehezítés: a mérések összeállítása nem függhet a korábbi mérések eredményétől, előre meg kell mondanunk, hogy az egyes mérésekben mely golyókat tesszük a két serpenyőbe.
|
| Előzmény: [17] lorantfy, 2003-11-05 10:21:31 |
|
| [19] Kós Géza | 2003-11-05 11:58:49 |
 Megkértem az e-mailben küldött megoldás szerzőit, hogy másolják be ide a megoldásukat és itt vitassuk meg. (Szerencsésebb, ha nem én másolgatok be ide e-maileket.)
|
| Előzmény: [18] Kós Géza, 2003-11-05 11:36:33 |
|
| [18] Kós Géza | 2003-11-05 11:36:33 |
 Azt javaslom, hogy a megoldásokat is ide írjuk, ne tördeljük szét a témát többfelé. Én az emberevős feladatra kaptam egy megoldást e-mailben, mindjárt ide másolom.
|
|
| [17] lorantfy | 2003-11-05 10:21:31 |
 Segítség a biliárdgolyós feladathoz: 3 csoportra osztjuk a 12 golyót. Összemérjük az első két csoportot. Ha egyenlő akkor innen már 2 méréssel a könnyű a dolgunk, ha felhasználjuk, hogy az első 8 golyó biztosan "jó". Ha az első mérésnél nem egyenlő a két csoport akkor figyelembe véve, hogy a mérleg merre billent le egy különleges mérést kell összeállítanunk, ahol a mérleg kibillenésének irányából is információkat tudunk szerezni. Na erre kell neked rájönni!
|
|
| [16] SchZol | 2003-11-04 20:14:40 |
 Sziasztok!
Én már megoldottam a billiárdgolyós példát, pont ma jött meg Lórántfytól a könyv, amit felajánlott. Szívesen leírom a megoldásom, ha kell.
Üdv,
Zoli
|
|
|
| [14] Frenky | 2003-11-04 17:18:34 |
 Üdv! JAJJ ez a billiárdgolyós példa.... érmével ismerem de végülis teljesen mindegy vagy egy hétig gondolkoztam rajta de nem sikerült.... mondjuk helyenként már elég sokáig eljutottam, sőt azt hittem sikerült, de aztán persze nem... na ennek egyszer beírhatnánk a megoldását...:-) mert az életben rá nem jövök...
|
|
|
| [12] Kós Géza | 2003-11-04 14:53:11 |
 Szia Laci,
Jó kérdés. :-)
Szerintem nem mindegy, hogy ismered a feladatot és a megoldást, vagy te találod meg. Ha te oldod meg elsőnek, és beírod a megoldást, az egyfajta dicsőség, de az is igaz, hogy nem mindig jó túl hamar lelőni a megoldást. Ha viszont ismered és úgy lövöd le, akkor...
Talán úgy kellene felfogni, mintha egy asztaltársaságban ülnénk egy pofa sökóla mellett :-). Ott sem mindig jó azonnal bedobni a megoldást, hagyni kell a többieket is gonsolkodni.
Ha viszont egy feladatot régóta nem oldottak meg, akkor lehet kérni, hogy valaki, aki ismeri, írja le. Én már régóta várom, hogy a 4. feladatot megoldja valaki, mert van egy kicsit nehezebb változata is, amit szeretnék majd feladni.
Üdv.
Géza
|
| Előzmény: [11] enel, 2003-11-04 14:32:31 |
|
| [11] enel | 2003-11-04 14:32:31 |
 Sziasztok! Nekem egy régi problémám, hogy ha egy feladatnak tudom a megoldását (mindegy, hogy most oldottam meg vagy korábban) akkor mikor "illik" (ha egyáltalán illik) beírni egy fórumra. Utálom, ha hamar megmondják a megoldást, Magam szeretem megoldani a fejtöro"ket, feladványokat. Ez annyira így van, hogy ha egy vicc kérdéssel indul, akkor arra is próbálok "megfelelni". Mesélek egy példát: Két függvény sétál a sivatagban. Odaugrik a rablófüggvény és rájuk ordít. "Adjátok ide az értékkészleteiteket, mert különben lederivállak benneteket!" Erre az egyik függvény elkezd kuncogni. Miért?
|
|
| [10] Mate | 2003-11-04 13:05:56 |
 Sziasztok! Úgy látom, ma gyereknap van, úgyhogy ha valaki megcsinálja a novemberi számban kitűzendő elektrosztatika-feladatomat integrálszámítás nélkül, vendégem egy somlói galuskára, és megkapja a Rácz Béla által felajánlott tábla csokit (ugyanis a Tom and Jerry példát úgysem oldja meg senki...)Vigh Máté:))
|
|
| [9] Rácz Béla | 2003-11-04 00:33:05 |
 Jó, én pedig felajánlok minimum 1 tábla csokit annak, aki elsőként megoldja Kós Géza: Tom és Jerry c. feladatkölteményét (Kömal 2003/5.) - Természetesen csak akkor, ha nem maga Géza az illető.
|
|
|
|
| [6] SchZol | 2003-11-01 22:12:06 |
 5.feladat:
Adott 100 láda mindegyikben 1000db 2grammos 1 forintos, kivéve egyett amiben 1grammosak az 1 forintosok. Legkevesebb hány mérésből tudjuk eldönteni melyik ládában vannak a selejtes egy forintosok, ha minden láda ugyanúgy néz ki, és csak egy egykarú mérlegünk van.
Szívesen fogadom a megoldásokat emailben.
Zoli
|
|
| [5] lorantfy | 2003-10-31 23:34:57 |
 4.feladat: Van 12 db biliárdgolyó mindegyik ugyanolyan színű és formájú csak az egyiknek a súlya eltér a másiktól. Azt nem lehet tudni hogy könnyebb vagy nehezebb. A feladat a következő: Hogyan tudod megállapítani biztosan hogy melyik a kakukktojás, ha van egy kétkarú mérleged és csak 3-szor mérhetsz vele? Az első e-miles megoldónak Gazsó Zoltán: "Visual" Adatbázis kezelők objektum-orientált programozása c. könyvét tudom felajánlani vagy egy tábla csokit.
|
|
| [4] Lóczi Lajos | 2003-10-31 20:12:50 |
 Kedves Sirpi,
nem tudom, hogy eldöntöttétek-e már, ebbe a rovatba várjunk-e megoldásokat (vagy csak bizonyos idő után), esetleg nyissunk egy új témát külön a megoldásoknak, hogy ne lőjük le a poént...szóval ha van elképzelés erről bárki részéről, írja meg.
Lajos
|
| Előzmény: [1] Sirpi, 2003-10-30 10:07:33 |
|
| [3] Kós Géza | 2003-10-30 11:08:09 |
 3. feladat. Az Óperenciás tenger közepén áll az Emberevők Szigete. Ez a sziget kör alakú, s partja mentén pontosan 26 falu található, lakosaik pogányok. A falvak nevei sorra az angol ábécé 26 betűjével kezdődnek (ciklikus sorrendben). A szigetet történelme folyamán pontosan 26 angol hittérítő kereste fel, ezek nevei is az angol ábécé különböző betűivel kezdődtek. Minden hittérítő először abba a faluba ment, amely nevének kezdőbetűje az ő neve kezdőbetűjével megegyezett. A szigeten egyszerre több hittérítő is tartózkodhatott, de egy faluban egyszerre csak egy. Ha egy hittérítő olyan faluba ért, amelynek lakosai éppen pogány hiten voltak, akkor megtérítette őket, és tovább ment a tengerpart mentén a következő faluba úgy, hogy a tenger jobb kéz felől essen. Ha viszont megtérített faluba ért, akkor a falu lakosai visszatértek a pogánysághoz és felfalták a szerencsétlent.
A hittérítők sorsa nem kétséges, de vajon milyen hiten vannak a falvak a hittérítők működése után?
(A feladat a KöMaL 1983. áprilisi számában jelent meg.)
|
|
| [2] Fálesz Mihály | 2003-10-30 10:22:23 |
 Javaslom, hogy számozzuk a feladatokat, ahogyan az két azonos nevű uralkodótól (vagy éppen világháborútól) kezdve szokás. :-)
Szóval, hátha valaki nem ismeri ezt a több, mint száz éves feladatot, amely a nagy Samuel Lloydtól származik.
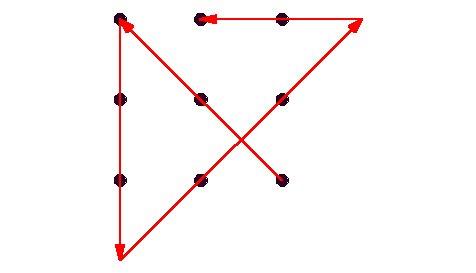
2. feladat. A képen 9 pont látható; egy négzet csúcsai, középpontja és oldalfelező pontjai. Rajzoljunk olyan folytonos töröttvonalat, amely csupán 4 (négy), egymáshoz csatlakozó szakaszból áll, és mindegyik ponton átmegy.
(Nem csalás, nem ámítás, ilyen töröttvonal tényleg létezik!)
|
 |
|
| [1] Sirpi | 2003-10-30 10:07:33 |
 Ha valakinek van valami jó matekpéldája, amit érdemesnek tart a többiekkel megosztani, akkor ide bátran beírhatja. Aktív KöMaL feladatokat légyszi ne irjatok be! Következzen elsőnek egy saját feladatom, azért is, hogy a TeX-et gyakoroljam: Biz. be: 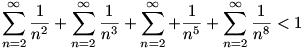
Sirpi |
|
















 =80o,
=80o,  =60o,
=60o,  =50o -- ha nem tévedek, ezekre gondoltál --, majd algebrai egyszerűsítések után a keresett
=50o -- ha nem tévedek, ezekre gondoltál --, majd algebrai egyszerűsítések után a keresett  szögre 80o adódik.
szögre 80o adódik. =50
=50 ADB
ADB x.
x. 








 2 természetes számra
2 természetes számra 


 3, akkor ez legalább 12 eset, amit nem lehet 2 mérésből megkülönböztetni. Ha k
3, akkor ez legalább 12 eset, amit nem lehet 2 mérésből megkülönböztetni. Ha k
