New exercises and problems in Mathematics
May
2001
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in May 2001 |
C. 630. In a 4-digit number, the sum of the first two digits is equal to that of the last two digits. The sum of the first and last digits is equal to the third digit. Finally, the sum of the second and fourth digits is twice the sum of the other two digits. Which number has all these properties?
C. 631. Determine the value of c so that the area enclosed by the graphs y=|x-1|+|x+1| and y=c is 30.
C. 632. The sequence 3, 15, 24, 48, ... contains those multiples of 3, in increasing order, which are 1 less than a perfect square. Determine the remainder when the 2001st term of the sequence is divided by 1000.
Proposed by Zs. Magyar, Budapest
C. 633. Each face of a tetrahedron has the same area, moreover, they all have equal inradii. Prove that the faces are all congruent.
C. 634. A 1 litre measure is in the shape of a frustum of a cone. Half a litre can be measured at the 2/3 of the altitude of the frustum. Find the ratio of the diameters of the bases.
 |
New problems in May 2001 |
B. 3462. Determine those positive integers n for which 100 can be expressed in the form \(\displaystyle \pm1\pm2\pm\dots\pm n\). (3 points)
B. 3463. The diameter of a half disc shaped sponge is 20 cm. A corner of a room is wiped with the sponge so that the two extremal points of its diameter touch the two perpendicular walls all the time. Determine the area one can wipe this way. (3 points)
B. 3464. A number has n digits which add up to 9n-8. How many such n-digit numbers are there? (4 points)
B. 3465. Let m, n be positive integers, and set the points E and F on side AB of a unit square ABCD such that AE=1/n and BF=1/m. Determine m and n such that the line through B that forms an angle of 30o with AB touches the semicircle drawn inside the square with diameter EF. Is it possible that AC touches the semicircle at the same time? (3 points)
Proposed by B. Bíró, Eger
B. 3466. In the plane a square ABCD is
given. Determine the locus of those points P for which sin(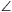
APB)=sin(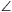DPC). (4 points)
B. 3467. Find the maximum of the function x(1+x)(3-x) on the set of positive numbers, without using calculus. (4 points)
B. 3468. No three diagonals of a convex 10-gon intersect at the same point. A point P is given inside the polygon such that P is not incident to any diagonal of the polygon. Prove that there are at least 28 ways to select 4 vertices of the polygon such that P is inside the quadrilateral determined by these points. (5 points)
B. 3469. Find those continuous functions f, for which f(f(x))=f(x)+x for every real number x. (5 points)
Gillis-Turán Mathematics Competition, 2001
B. 3470. Find an equation for the line that touches the curve y=3x4-4x3 at two different points. (4 points)
B. 3471. An ant is walking inside the region bounded by the curve whose equation is x2+y2+xy=6. Its path is formed by straight segments parallel to the coordinate axes. It starts at an arbitrary point on the curve and takes off inside the region. When reaching the boundary, it turns by 90o and continues its walk inside the region. When arriving at a point on the boundary which it has already visited, or where it cannot continue its walk according to the given rule, the ant stops. Prove that, sooner or later, and regardless of the starting point, the ant will stop. (5 points)
Gillis-Turán Mathematics Competition, 2000
 |
New advanced problems in May 2001 |
A. 266. Points A1, A2, A3, B1, B2, B3 lie on a circle. Let, for any 0<t<1 and i=1, 2, 3, Ci(t) and Di(t) denote the two points that divide the segment AiBi in the ratio t:(1-t). Let e(t) denote the radical axis of the circumcircles of triangles C1(t)C2(t)C3(t) and D1(t)D2(t)D3(t) (if it exists). Prove that the lines e(t) are either parallel or concurrent.
A. Dőtsch, Szeged
A. 267. Let m, n be positive integers and let 0\(\displaystyle le\)x\(\displaystyle le\)1. Prove that (1-xn)m+(1-(1-x)m)n\(\displaystyle ge\)1.
10th Vojtech Jarnik Mathematical Competition, Ostrava, 2000
A. 268. Let us choose arbitrarily n vertices of a regular 2n-gon and colour them red. The remaining vertices are coloured blue. We arrange all red-red distances into a nondecreasing sequence and do the same with blue-blue distances. Prove that the two sequences hence obtained are identical.
10th Vojtech Jarnik Mathematical Competition, Ostrava, 2000
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: solutions@komal.elte.hu.