Matematikából kitűzött gyakorlatok és feladatok
2001. május

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött (könnyebb) gyakorlatok

C. 630. Egy négyjegyű szám első két számjegyének összege egyenlő az utolsó két számjegy összegével. Az első és az utolsó számjegy összege a harmadik számjegyet adja. A második és negyedik számjegy összege az első és a harmadik összegének kétszerese. Melyik ez a négyjegyű szám?

C. 631. Az y=|x-1|+|x+1| függvény grafikonja és az y=c egyenletű egyenes által közrezárt síkidom területe 30. Mekkora a c állandó értéke?

C. 632. A 3, 15, 24, 48, ... sorozat a 3 azon többszöröseiből áll, amelyek 1-gyel kisebbek egy négyzetszámnál. Mennyi a maradék, ha a sorozat 2001-edik tagját elosztjuk 1000-rel?

Javasolta: Magyar Zsolt, Budapest

C. 633. Egy tetraéder lapjainak területe egyenlő, továbbá a háromszög lapok beírható köreinek sugarai is egyenlőek. Mutassuk meg, hogy a tetraéder lapjai egybevágóak.

C. 634. Csonkakúp alakú, felfelé szélesedő 1 literes háztartási mérőedényen a 1/2 liter jele az edény magasságának 2/3 részénél található. Mekkora az alapkör és a fedőkör átmérőjének aránya?

A B pontversenyben kitűzött feladatok

B. 3462. Milyen n-ekre érhető el, hogy a 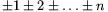alakú összegek között szerepeljen a 100? (3 pont)

B. 3463. Egy félkör alakú szivaccsal, amelynek átmérője 20 cm, végigtöröljük egy szoba padlójának egy sarkát úgy, hogy az átmérő két végpontja folyamatosan érinti a szoba derékszöget bezáró két falát. Mekkora területet töröl fel eközben a szivacs? (3 pont)

B. 3464. Hány olyan n-jegyű szám van, amelyben a számjegyek összege 9n-8? (4 pont)

B. 3465. Az egységoldalú ABCD négyzet AB oldalán lévő E és az F pontokra \(\displaystyle AE={1\over n}\) és \(\displaystyle BF={1\over m}\), ahol m és n pozitív egész számok. A B pontból kiinduló, AB-vel 30^o-os szöget bezáró egyenes érinti az EF, mint átmérő fölé, a négyzet belsejébe rajzolt félkört. Határozzuk meg az m és n értékét. Van-e a kapott számpárok között olyan, amely mellett a félkör érinti az AC átlót is? (3 pont)

Javasolta: Bíró Bálint, Eger

B. 3466. Határozzuk meg az ABCD négyzet síkjában azon pontok mértani helyét, amelyekre sin APB\(\displaystyle szog\)=sin DPC\(\displaystyle szog\). (4 pont)

B. 3467. Keressük meg az x(1+x)(3-x) kifejezés maximumát a pozitív számok körében a differenciálszámítás alkalmazása nélkül. (4 pont)

(A feladat megoldása előtt ajánljuk Csete Lajos 267. oldalon kezdődő cikkének elovasását.)

B. 3468. Egy konvex tízszög semelyik három átlója sem megy át egy ponton, és egy, a sokszög belsejében lévő P pont egyik átlón sincs rajta. Mutassuk meg, hogy a sokszög csúcsai közül legalább 28-féleképpen választható ki négy úgy, hogy az általuk meghatározott négyszög tartalmazza P-t. (5 pont)

B. 3469. Határozzuk meg mindazokat a folytonos f függvényeket, amelyekre f(f(x))=x+f(x) minden x valós számra. (5 pont)

Gillis-Turán matematikaverseny, 2001

B. 3470. Írjuk föl annak az egyenesnek az egyenletét, amely az y=3x⁴-4x³ egyenletű görbét két különböző pontban érinti. (4 pont)

B. 3471. Egy hangya mászkál az x²+y²+xy=6 egyenletű görbe által határolt területen. Útvonala a koordinátatengelyekkel párhuzamos egyenes szakaszokból áll. A hangya a görbe tetszőleges pontjából kiindulva addig megy egyenesen a görbe belsejében, amíg újra eléri a görbe határát. Ekkor 90^o-kal elfordul és folytatja útját a görbe belsejében. A hangya csak akkor áll meg, ha olyan határponthoz ér, amelyben már járt, vagy ha nem tudja útját a fenti szabálynak megfelelően folytatni. Bizonyítsuk be, hogy függetlenül a kiindulási ponttól a hangya előbb-utóbb megáll. (5 pont)

Gillis-Turán matematikaverseny, 2000

A pontversenyben kitűzött nehezebb feladatok

A. 266. Az A₁, A₂, A₃, B₁, B₂, B₃ pontok egy körön helyezkednek el. Tetszőleges 0<t<1 valós számra legyen C_i(t) és D_i(t) az A_iB_i szakaszt t:(1-t) arányban osztó pont (i=1, 2, 3). Legyen e(t) a C₁(t)C₂(t)C₃(t) és D₁(t)D₂(t)D₃(t) háromszögek körülírt köreinek hatványvonala (ha létezik).

Igazoljuk, hogy az e(t) egyenesek vagy párhuzamosak, vagy egy ponton mennek át.

Dőtsch András, Szeged

A. 267. Legyen m, n pozitív egész és 0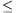x\(\displaystyle le\)1. Igazoljuk, hogy

Vojtech Jarnik emlékverseny, Ostrava, 2000

A. 268. Egy szabályos 2n-szög n csúcsát pirosra, a többi csúcsát kékre színeztük. Nagyság szerint sorbarendezzük az összes piros pontpár távolságát, és nagyság szerint sorbarendezzük az összes kék pontpár távolságát is. Bizonyítsuk be, hogy az így kapott két, 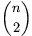hosszúságú számsorozat ugyanaz.

Vojtech Jarnik emlékverseny, Ostrava, 2000

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2001. június 15.