A 2001. szeptemberi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 635. Számtanórán megkérdezték a gyerekeket, hogy hány lába van összesen egy tyúknak, hat kutyának és hét palpigradinak (a palpigradi egy állat latin neve). Aladár szerint 46, Benő szerint 52, Cecília szerint 66, Dóra szerint 78, Eufrozina szerint pedig 82. Melyiküknek van igaza?

Zrínyi verseny feladata alapján

Megoldás. Ha a palpigradi lábainak száma x, akkor a lábak száma összesen 2+6^.4+7^.x=7(x+3)+5. A lábak száma tehát 7-tel osztva 5-öt ad maradékul. A 46, 52, 66, 78 és 82 számok közül csak a 82 ad 5-öt maradékul 7-tel osztva, tehát csak Eufrozinának lehet igaza.

A 2+6^.4+7^.x=82 egyenletet megoldva azt is megtudhatjuk, hogy a palpigradinak 8 lába van.

C. 636. Ábrázoljuk a derékszögű koordinátarendszerben azokat a pontokat, amelyek koordinátáira

-2$\displaystyle le$x$\displaystyle le$2, -3$\displaystyle le$y$\displaystyle le$3, {x} $le$ {y}.

(A {z} a z szám törtrészét jelöli.)

Megoldás. Az egységnégyzet belsejében levő pontokra a harmadik egyenlőtlenségben a törtrész jele elhagyható, hiszen itt a pontok koordinátái megegyeznek a törtrészükkel. Ezért elég azt nézni, hogy mely pontok koordinátáira teljesül az, hogy x $le$ y. Ezek pontok az y=x egyenletű egyenesen, illetve fölötte levő pontok. Az egységnégyzet függőleges oldalai és csúcsai, ahol {x}=0, a halmazhoz tartoznak; vízszintes oldalainak belső pontjai, ahol {y}=0, nem. A többi négyzetben ugyanilyen ábrákat kapunk.

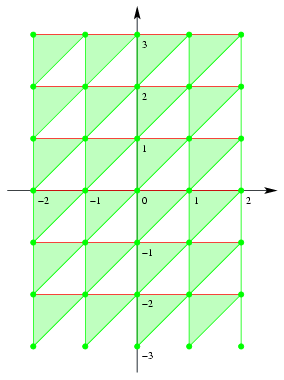
Figyelembe véve az első és a második egyenlőtlenséget a következő halmaz adódik. (A halmaz a zöld színnel jelölt háromszögekből, szakaszokból és pontokból áll; a piros színnel jelölt szakaszok nem tartoznak a halmazhoz.)

C. 637. Melyik az a pozitív egész szám, amely a tízes és a nyolcas számrendszerben is háromjegyű, továbbá számjegyeinek összege mindkét esetben tizennégy?

Megoldás. Írjuk fel a szám mindkét alakját:

a^.10²+b^.10+c=x^.8²+y^.8+z.

Mindkét oldalból vonjunk ki a számjegyek összegét, 14-et:

99a+9b=63x+7y.

Kivonva 63x-et,

99a+9b-63x=7y.

Ennek bal oldala osztható 9-cel, ezért a jobb oldala is. Így y értéke 9 vagy 0. De nyolcas számrendszerben nincs 9-es számjegy. Ezért y értéke 0.

Az x+y+z=14 feltétel miatt x+z=14. Mivel x és z legfeljebb 7 és összegük 14, azért x is és y is 7-tel egyenlő. A keresett szám tehát 8-as számrendszerben 707, ami a 10-es számrendszerben 455.

C. 638. Hány olyan négyzetes oszlop van, amelyben az élek cm-ben mért mérőszáma egész szám, és a felszín mérőszáma cm²-ben megadva annyi, mint a térfogat mérőszáma cm³-ben megadva?

Megoldás. Jelöljük n-nel a négyzetes hasáb alapélét, a magasságát pedig k-val. A térfogat és a felszín egyenlőségéből

n²k=2n²+4nk.

Ezt n-nel osztva és rendezve:

nk-2n-4k=0.

Adjunk mindkét oldalhoz 8-at, a baloldal így szorzattá alakítható:

(n-4)(k-2)=8.

A 8 lehetséges szorzattá alakításai: 8^.1,4^.2,2^.4,1^.8. Negatív tényezők nem jöhetnek szóba, mert n-4>-4 és k-2>-2. Ebből (n,k)-ra négy megoldást kapunk: (12,3); (8,4); (6,6) és (5,10). A feltételeknek tehát négyféle oszlop tesz eleget.

C. 639. Hány olyan pozitív egész számokból álló (a;b) számpár van, amelyre

1$\displaystyle le$a$\displaystyle le$2001, 1 $le$ b$\displaystyle le$2001,

és az a és b számok legkisebb közös többszöröse 2001?

Megoldás. A 2001 törzstényezős felbontása 3^.23^.29. A két szám prímtényezős alakja tehát: a=3^k^.23^m^.29ⁿ, illetve b=3^p^.23^q^.29^r, ahol mindegyik kitevő 0 vagy 1 lehet.

A (k,p), (m,q) és (n,r) párok három-háromfélék lehetnek: (0,1), (1,0) és (1,1); a (0,0) nem lehetséges. A három kitevőpárt egymástól függetlenül választhatjuk ki. Ha például a három kitevőpár (0,1), (1,1) és (0,1), akkor az a=3⁰^.23¹^.29⁰, b=3¹^.23¹^.29¹ számpárt kapjuk.

Ezért a lehetséges (a,b) számpárok száma 3³=27.

Már regisztráltál?
Új vendég vagy?