A 2001. szeptemberi informatika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

I. 1. A KöMaL honlapján megtalálható Bölcsföldi József és Balázs Géza (Perczel Mór Gimnázium, Siófok) cikke a barátságos számokról:

,,Pitagorasz óta ismeretes, hogy a és b természetes számok barátságos számpárt alkotnak, ha a önmagától különböző osztóinak összege b, és b önmagától különböző osztóinak összege a. A barátságos számpár tagjai közül az egyik értelemszerűen osztódús (megvastagított szám), a másik osztószegény. Ezek a párok a következők:
(220, 284), (1184, 1210), (2620, 2924), (5020, 5564), (6232, 6368), (10 744, 10856).''

Készítsünk programot, amely beolvas két természetes számot (N<M<1 000 000), majd kiírja azon (b_i, b_j) barátságos számokat, amelyekre N<b_i, b_j<M. (10 pont)

Egyszerűsített algoritmus:

Algoritmus Barátságos_számok;
  Be: N, M
Első lépés az intervallum beolvasása,
  Ciklus I:=N-től M-ig
melynek minden elemére meg kell nézni: van-e intervallumbeli barátságos párja.
    K:=1; J:=2;
K lesz az osztók összege, J pedig az éppen vizsgált osztó.
    Ciklus amíg J*J<I
      Ha I mod J=0 akkor K:=K+J+I div J;
      J:=J+1;
Addig kell ismételnünk az osztók összeadását, amíg az osztó kisebb, mint a szám gyöke. Az osztót (a szám osztható vele, vagyis a vele való osztás után a maradék 0) és az osztás eredményét is hozzáadjuk az összeghez.
    Ciklus vége
    Ha (J*J=I) ÉS (I mod J=0) akkor K:=K+J
Abban az esetben, ha a szám éppen négyzetszám (J*J=I), akkor csak az osztót (J) kell egyszer hozzáadni.
    Elágazás vége
   Ha (K>I) ÉS (K<=M)
Ha az osztók összegét, K-t még nem ellenőriztük, vagyis nagyobb, mint az I (K>I) de még az intervallum eleme, akkor meg kell néznünk, hogy barátságos-e K az I-hez, vagyis K önmagától különböző osztóinak összege I-e. (Hatékonyság szempontjából persze ez nem a legjobb, mert így ezeket a számokat többször megnézzük. Hiszen akkor is, amikor az majd sorra kerül.)
      akkor L:=1; J:=2;
Ugyanúgy végezzük az osztó összegének kiszámolását, mint az előbb. L lesz az osztók összege, J pedig az éppen vizsgált osztó.
        Ciklus amíg J*J<K
          Ha K mod J=0
            akkor L:=L+J+K div J;
          Elágazás vége
          J:=J+1;
Addig kell ismételnünk az osztók összeadását, amíg az osztó kisebb, mint a szám gyöke. Az osztót (a szám osztható vele, vagyis a vele való osztás után a maradék 0) és az osztás eredményét is hozzáadjuk az összeghez.
        Ciklus vége
        Ha (J*J=K) ÉS (K mod J=0)
          akkor L:=L+J;
Abban az esetben, ha a szám éppen négyzetszám (J*J=K), akkor csak az osztót (J) kell egyszer hozzáadni.
        Elágazás vége
        Ha I=L
          akkor Ki:I,K
Akkor kell kiírni a barátságos számpárt, ha azok önmagától különböző osztóinak összege a másik. Vagyis I önmagától különböző osztóinak összege K, ennek az önmagától különböző osztói pedig L. Vagyis, ha I=L.
        Elágazás vége
    Elágazás vége
  Ciklus vége
Eljárás vége

Turbo Pascal program:

Program baratsagos;
  uses newdelay,crt;
  var i,j,k,l,n,m: longint;
begin
  clrscr; writeln('Baratsagos szamok'); writeln;

  writeln('Mettol?'); readln(n);
  writeln('Meddig?'); readln(m);
  for i:=n to m do
  begin
    k:=1; j:=2;
    while j<sqrt(i) do
    begin
      if i mod j=0 then k:=k+j+i div j;
      j:=j+1;
    end;
    if (j=sqrt(i)) and (i mod j=0) then k:=k+j;
    if (k>i) and (k<=m) then
    begin
      l:=1; j:=2;
      while j<sqrt(k) do
      begin
        if k mod j=0 then l:=l+j+k div j;
        j:=j+1;
      end;
      if (j=sqrt(k)) and (k mod j=0) then l:=l+j;
      if i=l then writeln(i,'-',k);
    end;
  end;
  readln;
end.

I. 2. A programozási nyelvek többsége képes arra, hogy egyetlen utasítással egy ellipszist rajzoljunk a képernyőre. Ez azonban csak olyan ellipszis lehet, amelynek tengelyei párhuzamosak a képernyő széleivel.

Készíts programot, amely tetszőleges állású ellipszist képes a képernyőre rajzolni! Paraméterként adjuk meg a két tengely hosszát, valamint a nagytengely és a képernyő felső széle által bezárt szöget fokban! (10 pont)

Megoldás:

Algoritmus Ellipszis(a,b,szög:Valós),

ahol a a nagytengely, b a kistengely és szög az elforgatás szöge.
  c_szög:=0;
  Ciklus amíg c_szög<180
Egy rajzoláskor két pontot rajzolunk ki. Így addig kell rajzolni, amíg az ellipszis feléig el nem jutunk a szög szerinti bejárás során.
    r:=a*b / sqrt(b*b*cos(pi*c_szög/180)*cos(pi*c_szög/180)+
                  a*a*sin(pi*c_szög/180)*sin(pi*c_szög/180));
r a távolságot jelenti a polárkoordinátás felírásban. Ennek levezetése a következő: x=rcos $alpha$ és y=rsin $alpha$ felhasználásával az ellipszis egyenlete $1={x^2\over a^2}+{y^2\over b^2}={r^2\cos^2\alpha\over a^2}+{r^2\sin^2\alpha\over b^2}$ , így $\displaystyle r^2={1\over{{\cos^2\alpha\over a^2}+{\sin^2\alpha\over b^2}}}$, illetve $\displaystyle r={ab\over\sqrt{b^2\cos\alpha+a^2\sin^2\alpha}}$.
    x:=r*cos(pi*(c_szög-szög)/180);
    y:=r*sin(pi*(c_szög-szög)/180);
A polárkoordináták visszaszámolása már egyszerű az elforgatással együtt.
    PontRajzolás(MaxX div 2 + Trunc(x),MaxY div 2 + Trunc(y));
    PontRajzolás(MaxX div 2 - Trunc(x),MaxY div 2 - Trunc(y));
A programozási nyelvek tudnak pontot rajzolni. Az x és y koordinátákat csak a képernyő közepére kell tolni.
    epszilon:=arctan(1/sqrt(x*x+y*y));
    c_szög:=c_szög+epszilon;
Az utolsó lépés a következő pont kiszámolása előtt a szögelfordulás és vele együtt az új szög kiszámolása. $epszilon$ -t forduljunk el, ami legyen a legkisebb olyan szög, ami már észrevehető, tehát a szomszédos képkockába esik, de nem hagy üresen szomszédos pixelt. Vagyis 1 képkockát lép merőlegesen a középponttól húzott szakaszra. Az utóbbi hossza éppen $\displaystyle \sqrt{x^2+y^2}$
  Ciklus vége;
Eljárás vége;{_Ellipszis}

I. 3. Megtakarított pénzünket N (1$\displaystyle le$N$\displaystyle le$10) éven keresztül egy bankba rakjuk az alábbi módon:

1. N éven keresztül minden hónap elején beteszünk A forintot, és egy évre X százalékos kamattal (X>0, valós szám) lekötjük.

2. A lekötés lejártakor, a következő hónap elején kapjuk meg az éves kamatot, ekkor a bent levő pénzt a kamattal együtt egy évre újra lekötjük.

Készítsünk táblázatot (PENZ.XLS), amelybe egy adott helyre beírva N, A és X értékét, N éven keresztül kiszámolja, hogy mennyi pénzünk van a bankban! A táblázatban pontosan N sor szerepeljen, azaz ha N-et változtatjuk, akkor a felesleges sorok ne látsszanak!

Példa: (N=3, A=1000, X=10 esetén)

1. év: 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 11000 12000

2. év: 13100 14200 15300 16400 17500 18600 19700 20800 21900 23000 24100 25200

3. év: 26410 27620 28830 30040 31250 32460 33670 34880 36090 37300 38510 39720

(10 pont)

Megoldás.

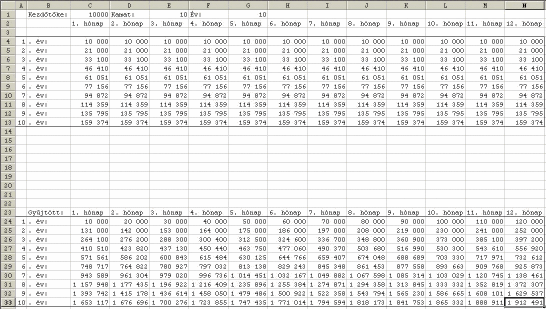
A statikus, mindig állandó tartalmú cellák rendben vannak. A dinamikusan változó cellák esetén függvényeket kell használni, mely kifejezéseknek az értéke jelenik meg.

A feladat megoldásában csak akkor jelenjen meg valami a cellában, ha az adott cella a még kiírandó év sorában van. Tehát aszerint üres vagy van valami a cellában, hogy az adott sor hol van. Ezt a HA(feltétel; igaz esetén része; hamis esetén része) függvény segítségével tudjuk megtenni. Fogalmazzuk meg a feltételt. Ehhez segítségül kell még egy függvény hívnunk, mégpedig a SOR(cella) függvényt, mely az adott cella sorának sorszámát adja meg. Tehát mindig az lesz a feltételünk, hogy az adott cella sora hányadik, és ha még ki kell írni, akkor kiírjuk, különben nem jelenik meg semmi. Vagyis ha az év sorszáma (sor sorszáma mínusz a kezdés) kisebb vagy egyenlő a kiírandó évek számánál (ez mindig a G1-es cellában helyezkedik el, ezért kell a $-jel a sor és oszlop jelzés elé is.)

Az, hogy mi jelenik meg már nehezebb kérdés. A feladatot két fő részre osztjuk, és a két táblában is három-három oszlopra írunk fel feltételes kiírást. Az első és második oszlopban, mindkét tábla esetén csak annyi szerepel, hogy az adott év sorszáma, illetve a ". év:" megjelenik-e vagy sem, az előbb tárgyalt feltétel esetén.

Most jön a feladat neheze. Az első táblázatban megadjuk, hogy adott év (sor) adott hónapjában (oszlop/cella) mennyi az akkor lejárt pénzösszeg, az újonnan betett tőke és a kamat összege. A második táblázatban van a gyűjtött pénz értékei. Egy év adott hónapjában, a bankba levő pénzünk mennyiségét az első táblázat segítségével számoljuk ki. Mégpedig úgy, hogy az adott évben (sor) az adott hónapig (oszlop/cella) mennyi az első táblában levő értékek összege, és még kellenek az előző évből, a hiányzó hónapokhoz tartozó pénzösszegek.

Tehát a megoldás:

A4: "=HA(SOR(A4)-3<=$G$1;SOR(A4)-3;"")" A13-ig.

B4: "=HA(SOR(B4)-3<=$G$1;". év:";"")" B13-ig.

C4: "=HA(SOR(B4)-3<=$G$1;$C$1+C3*$E$1/100+C3;"")" N13-ig

A24: "=HA(SOR(A24)-23<=$G$1;SOR(A24)-23;"")" A33-ig

B24: "=HA(SOR(B24)-23<=$G$1;". év:";"")" B33-ig

C24: "=HA(SOR(B24)-23<=$G$1;SZUM(D3:$N3)+SZUM($C4:C4);"")" N33-ig

Már regisztráltál?
Új vendég vagy?