 |
A 2002. novemberi B-jelű matematika feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
B.3582. Oldjuk meg a természetes számok körében a
3xyz-5yz+3x+3z=5
egyenletet. (3 pont)
Megoldás: Hozzuk az egyenletet (3x-5)(yz+1)=-3z alakra. Mivel -3z\(\displaystyle le\)0 és yz+1>0, szükségképpen 3x-5\(\displaystyle le\)0, vagyis x értéke csak 0 vagy 1 lehet. Az első esetben az egyenlet (5y-3)z=-5 alakra hozható. Ekkor egyrészt z osztója 5-nek, másrészt mivel 5y-3 nem osztható 5-tel, szükségképpen z osztható 5-tel, tehát z=5, 5y-3=-1, ez azonban nem lehetséges. A második esetben az egyenletet (2y-3)z=-2 alakra hozhatjuk, ahonnan az előző okoskodáshoz hasonlóan z=2, 2y-3=-1 következik, így y=1. Az egyenlet egyetlen megoldása tehát x=y=1, z=2.
B.3583. Egy ABC háromszög beírt körének középpontját összekötöttük a háromszög csúcsaival. Az így kapott háromszögek közül az egyik hasonló az ABC háromszöghöz. Mekkorák az ABC háromszög szögei? (3 pont)
Megoldás: Legyenek a háromszög szögei \(\displaystyle alpha\),\(\displaystyle beta\),\(\displaystyle gamma\), a beírt kör középpontja K. Tegyük fel, hogy a BCK háromszög hasonló az ABC háromszöghöz. Ennek a háromszögnek a szögei, \(\displaystyle beta\)/2,\(\displaystyle gamma\)/2 és \(\displaystyle pi\)/2+\(\displaystyle alpha\)/2 valamilyen sorrendben megegyeznek az ABC háromszög szögeivel. Az nem lehet, hogy \(\displaystyle pi\)/2+\(\displaystyle alpha\)/2=\(\displaystyle alpha\), mert abból \(\displaystyle alpha\)=\(\displaystyle pi\) következne. Szimmetria okokból feltehetjük hát, hogy \(\displaystyle pi\)/2+\(\displaystyle alpha\)/2=\(\displaystyle gamma\). Mivel \(\displaystyle beta\)=\(\displaystyle beta\)/2 nem lehet, ezért \(\displaystyle beta\)=\(\displaystyle gamma\)/2 és \(\displaystyle alpha\)=\(\displaystyle beta\)/2, ahonnan
\(\displaystyle pi\)/2+\(\displaystyle alpha\)/2=\(\displaystyle gamma\)=2\(\displaystyle beta\)=4\(\displaystyle alpha\)
adódik. Ezek szerint a háromszög szögei \(\displaystyle alpha\)=\(\displaystyle pi\)/7, \(\displaystyle beta\)=2\(\displaystyle pi\)/7 és \(\displaystyle gamma\)=4\(\displaystyle pi\)/7.
B.3584. Írjuk le az egész számokat egyesével 1-től 10n-1-ig, és legyen az eközben leírt számjegyek száma A. Ezek után ismét írjuk le az egész számokat egyesével, ezúttal 1-től 10n-ig, és legyen az így leírt nullák száma B. Bizonyítsuk be, hogy A=B. (4 pont)
Megoldás: Jelölje Ai az 1-től 10n-1-ig leírt számok közül a legalább i-jegyűek számát, Bi pedig az 1-től 10n-ig leírt számok közül azoknak a számát, ahol hátulról az i-edik értékes jegy 0. Példaképpen: A1=B1=10n-1 és An=Bn=1. Mivel A=A1+A2+...+An és B=B1+B2+...+Bn, elég annyit megmutatni, hogy 1\(\displaystyle le\)i\(\displaystyle le\)n esetén Ai=Bi. Ez azonban nyilvánvaló, hiszen a szóban forgó számok között egy-egy értelmű megfeleltetést létesíthetünk a megfelelő helyre beillesztett 0 számjegy beiktatásával, illetve a fordított irányban, a megfelelő helyen álló 0 számjegy eltörlésével.
B.3585. Határozzuk meg az a paraméter azon értékeit, amelyekre az
\(\displaystyle \sqrt{1+x^4\)1-2ax+x^2">
egyenlőtlenség minden pozitív x-re teljesül. (3 pont)
XI. Nemzetközi Magyar Matematika Verseny
Megoldás: Ha a\(\displaystyle le\)0, akkor pozitív x esetén
\(\displaystyle 1-2ax+x^2\ge1+x^2=\sqrt{1+2x^2+x^4\)\sqrt{1+x^4},">
tehát az egyenlőtlenség nem teljesül. Ha a\(\displaystyle ge\)1 és x\(\displaystyle ge\)1, akkor
\(\displaystyle 1-2ax+x^2 \(\displaystyle 1-2ax+x^2<1<\sqrt{1+x^4},\)
a\(\displaystyle ge\)1 esetén tehát minden pozitív x szám kielégíti az egyenlőtlenséget.
A fennmaradó 0<a<1 esetet vizsgálva megállapíthatjuk, hogy pozitív x értékek esetén 1-2ax+x2>1-2x+x2\(\displaystyle ge\)0, és ezért ekkor a szóban forgó egyenlőtlenség sorra ekvivalens az
1+x4>(1-2ax+x2)2,
4ax3-4a2x2-2x2+4ax>0,
\(\displaystyle x^2-{2a^2+1\over2a}x+\)0,">
\(\displaystyle \Bigl(x-{2a^2+1\over4a}\Bigr)^2+1-\Bigl({2a^2+1\over4a}\Bigr)^\)0">
egyenlőtlenségekkel. Ez utóbbi pontosan akkor teljesül minden pozitív x-re, ha a pozitív \(\displaystyle x={2a^2+1\over4a}\) esetén is teljesül, vagyis ha
\(\displaystyle 1-\Bigl({2a^2+1\over4a}\Bigr)^\)0,">
vagy ami ezzel ekvivalens, 4a>2a2+1. Ez utóbbi pedig pontosan akkor teljesül, ha \(\displaystyle 1-\sqrt{2}/2 B.3586. Az a paraméter mely
értékeire van a lg(ax)=2lg(x+1) egyenletnek pontosan egy
megoldása? (4 pont) Megoldás: Ha x megoldása az egyenletnek, akkor szükségképpen ax>0 és x>-1. Ezen feltételek mellett az egyenlet ekvivalens az ax=(x+1)2 egyenlettel. Ezt átalakítva az x2+(2-a)x+1=0 egyenlethez jutunk, melynek diszkriminánsa D=a2-4a. Ha D<0, akkor az egyenletnek nincs megoldása. Ha D=0, akkor vagy a=0, ami az ax>0 feltétel miatt nem jöhet szóba, vagy a=4, mely esetben az x2+(2-a)x+1=0 egyenlet megoldása x=1, mely egyben megoldása az eredeti egyenletnek is. D>0 pontosan akkor teljesül, ha a<0 vagy 4<a, mely esetben az x2+(2-a)x+1=0 egyenlet két megoldása
\(\displaystyle {a-2\pm\sqrt{a^2-4a}\over2}.\)
Ha a>4, akkor \(\displaystyle a-2=\sqrt{a^2-4a+4\)\sqrt{a^2-4a}"> miatt mindkét megoldás pozitív, így eleget tesz az ax>0 és x>-1 feltételeknek is. Ezek az a értékek tehát nem jöhetnek szóba.
Ha viszont a<0, akkor az ax>0 és x>-1 feltételek a -1<x<0 kikötésre redukálódnak. Most \(\displaystyle |a-2\)\sqrt{a^2-4a}"> miatt mindkét gyök negatív. A kisebbik gyök,
\(\displaystyle {a-2-\sqrt{a^2-4a}\over2}<{a-2\over2}<-1,\)
nem megoldása az eredeti egyenletnek. Azt kell tehát megvizsgálnunk, milyen a<0 esetén lesz
\(\displaystyle {a-2+\sqrt{a^2-4a}\over2\)-1,">
vagyis \(\displaystyle a-2+\sqrt{a^2-4a\)-2">, \(\displaystyle \sqrt{a^2-4a\)-a=\sqrt{a^2}">. Ez azonban a<0 esetén mindig teljesül.
Összefoglalva, az egyenletnek pontosan akkor van pontosan egy megoldása, ha a=4 vagy a<0.
B.3587. Adott gömb köré négyzet alapú, egyenes csonkagúlát írunk. Mekkora lehet a csonkagúla térfogatának és felszínének az aránya? (4 pont)
Megoldás: A gömb középpontját a csonkagúla éleivel összekötve a csonkagúla 6 négyszög alapú gúlára bontható fel. Mindegyik gúlának a magassága megegyezik a gömb sugarával, amit R-rel jelölünk. A gúlák alaplapja pedig a csonkagúla egy-egy lapjával egyezik meg. Ha a csonkagúla lapjai rendre A1,A2,...,A6 területtel bírnak, akkor az egyes gúlák térfogata V1=A1R/3, V2=A2R/3, ..., V6=A6R/3. Ezért a csonkagúla térfogata
\(\displaystyle V=V_1+V_2+\ldots+V_6={(A_1+A_2+\ldots+A_6)R\over3}={AR\over3},\)
ahol A éppen a csonkagúla felszíne. A szóban forgó arány tehát R/3, függetlenül attól, milyen csonkagúlát írtunk az R sugarú gömb köré.
B.3588. Adott egy kör és a belsejében az M pont. Egy M csúcsú derékszög szárai a kört az A és B pontokban metszik. Mi az AB szakasz felezőpontjának mértani helye, ha a derékszög körbefordul az M pont körül? (4 pont)
Megoldás: Jelölje az adott k kör középpontját O, az (esetleg elfajuló) OM szakasz felezőpontját K, az AB szakasz felezőpontját pedig F. Jelölje továbbá a k kör sugarát r, az M pontnak a kör középpontjától mért távolságát pedig d. Azt állítjuk, hogy a keresett mértani hely egy olyan k* kör, melynek középpontja K, sugara pedig \(\displaystyle \sqrt{2r^2-d^2}/2\).
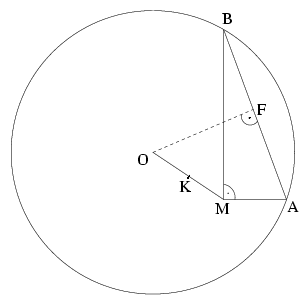
Először megmutatjuk, hogy F illeszkedik a k* körre. Mivel az FK szakasz az OMF háromszög súlyvonala, a jól ismert azonosság szerint (mely könnyen levezethető, ha az OKF és MKF háromszögek OF, illetve MF oldalára felírjuk a koszinusz-tételt)
\(\displaystyle KF^2={2OF^2+2MF^2-OM^2\over4},\)
ez az összefüggés nyilván teljesül az elfajuló O=M esetben is. Az AMB derékszögű háromszögből MF=FA=FB, az OFA derékszögű háromszögből pedig ezek után OF2+MF2=OF2+FA2=OA2=r2 adódik, ahonnan KF2=(2r2-d2)/4, ahogyan azt állítottuk.
Végül megmutatjuk, hogy a k* kör minden pontja megfelelő. Legyen F a k* kör tetszőleges pontja, és jelölje A és B az OF-re F-ben állított merőlegesnek a k körrel alkotott két metszéspontját, ekkor F nyilván az AB szakasz felezőpontja. Annyit kell tehát csak megmutatni, hogy az AMB szög derékszög. Azonban
\(\displaystyle MF^2={4KF^2+OM^2-2OF^2\over2}={2r^2-2OF^2\over2}=OA^2-OF^2=AF^2,\)
ahonnan FM=FA adódik. Ezért M rajta van az AB átmérőjű körön, tehát Thalesz tétele értelmében az AMB szög valóban derékszög.
B.3589. Bizonyítsuk be, hogy végtelen sok olyan n páratlan pozitív egész szám létezik, amelyre 2n+n összetett szám. (4 pont)
Megoldás: Megmutatjuk, hogy ha n 6k+1 alakú, akkor 2n+n osztható 3-mal. Ez k=0 esetén nyilván igaz, hiszen ekkor n=1, 2n+n=3. Ha pedig ak=26k+1+6k+1 osztható 3-mal, akkor ak+1 is osztható, ugyanis különbségük,
ak+1-ak=26k+7+6k+7-(26k+1+6k+1)=63.26k+1+6
szemlátomást osztható 3-mal. A teljes indukció elve miatt tehát az állítás igaz minden k természetes szám esetén. Továbbá ha k>0, vagyis n>1, akkor 2n+n>3. Megállapíthatjuk tehát, hogy minden olyan 1-nél nagyobb n pozitív egész számra, mely 6-tal osztva 1 maradékot ad, 2n+n összetett szám. Mivel végtelen sok ilyen szám van, és az egyben páratlan is, a feladatot megoldottuk.
B.3590. Az x3-10x+11=0 egyenlet gyökei u, v és w. Határozzuk meg az
arctg u+arctg v+arctg w
értékét. (5 pont)
Megoldás: Legyen u\(\displaystyle le\)v\(\displaystyle le\)w, \(\displaystyle \arctan u=\alpha\), \(\displaystyle \arctan v=\beta\) és \(\displaystyle \arctan w=\gamma\). Ekkor a gyökök és együtthatók közötti összefüggések felhasználásával tan\(\displaystyle alpha\)+tan\(\displaystyle beta\)+tan\(\displaystyle gamma\)=0, tan\(\displaystyle alpha\)tan\(\displaystyle beta\)+tan\(\displaystyle beta\)tan\(\displaystyle gamma\)+tan\(\displaystyle gamma\)tan\(\displaystyle alpha\)=-10 és tan\(\displaystyle alpha\)tan\(\displaystyle beta\)tan\(\displaystyle gamma\)=-11. Így
\(\displaystyle \tan({\alpha+\beta+\gamma})={\tan(\alpha+\beta)+\tan\gamma\over1-\tan(\alpha+\beta)\tan\gamma}={\tan\alpha+\tan\beta+\tan\gamma-\tan\alpha\tan\beta\tan\gamma\over1-\tan\alpha\tan\beta-\tan\beta\tan\gamma-\tan\gamma\tan\alpha}=1.\)
Ezért \(\displaystyle \alpha+\beta+\gamma={\pi\over4}+k\pi\) valamely k egész számra.
Az x3-10x+11 polinom a -4,-3,1,2,3 helyeken rendre a -13,14,2,-1,8 értékeket veszi fel, ahonnan leolvasható, hogy -4<u<-3, 1<v<2 és 2<w<3, vagyis \(\displaystyle \arctan(-4)+\arctan1+\arctan2\approx0,5667<\alpha+\beta+\gamma<\arctan(-3)+\arctan2+\arctan3\approx1,1071\), ahonnan k=0, a keresett érték tehát \(\displaystyle {\pi\over4}\).
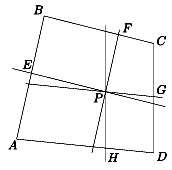
B.3591. A konvex ABCD négyszög
területe T, egy belső pontja P. A P-n
keresztül BC-vel húzott párhuzamos egyenes a BA oldalt
az E, az AB-vel húzott párhuzamos egyenes a BC
oldalt az F, az AD-vel húzott párhuzamos egyenes a
CD oldalt a G pontban, a CD-vel húzott párhuzamos
egyenes az AD oldalt a H pontban metszi. Jelölje az
AEPH négyszög területét t1, a PFCG
négyszög területét t2. Bizonyítsuk be, hogy 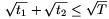 .
.
(5 pont)
Megoldás: Legyen AH=a, HD=PG=b, AE=c, EB=PF=d, CF=e, FB=PE=f, CG=g, GD=PH=h. Jelölje még a BAC és BCD szögeket rendre \(\displaystyle alpha\) és \(\displaystyle beta\). Ekkor a bizonyítandó állítás ekvivalens a
\(\displaystyle \sqrt{ac\sin\alpha+fh\sin\beta}+\sqrt{bd\sin\alpha+eg\sin\beta}\le\)
\(\displaystyle \le\sqrt{(a+b)(c+d)\sin\alpha+(e+f)(g+h)\sin\beta}\)
egyenlőtlenséggel. Mivel mindkét oldalon pozitív szám áll, ez tovább ekvivalens a négyzetreemelés és rendezés után nyert
\(\displaystyle 2\sqrt{(ac\sin\alpha+fh\sin\beta)(bd\sin\alpha+eg\sin\beta)}\le(ad+bc)\sin\alpha+(eh+fg)\sin\beta\)
egyenlőtlenséggel. Újabb ekvivalens átalakítást végrehajtva végül a
\(\displaystyle 0\le\Bigl((ad-bc)\sin\alpha+(eh-fg)\sin\beta\Bigr)^2+4(ag-bh)(df-ce)\sin\alpha\sin\beta\)
egyenlőtlenséghez jutunk. Most már csak az (ag-bh)(df-ce)\(\displaystyle ge\)0 egyenlőtlenséget kell igazolnunk.
Tegyük fel egy pillanatra, hogy a P pont az AC átlón helyezkedik el és azt p:q arányban osztja. Ekkor a párhuzamos szelők tétele miatt
a:b=p:q=c:d=f:e=h:g,
ahonnan ad=bc, eh=fg, ag=bh és df=ce következik. Ekkor tehát (ag-bh)(df-ce)=0, sőt (ad-bc)sin\(\displaystyle alpha\)+(eh-fg)sin\(\displaystyle beta\)=0 is igaz, így ekkor \(\displaystyle \sqrt{t_1}+\sqrt{t_2}=\sqrt{T}\). Megmutatjuk, hogy minden más esetben (ag-bh)(df-ce)>0, és ennek következtében a bizonyítandó állítás határozott egyenlőtlenséggel teljesül.
Tegyük fel, hogy a P pont az ADC háromszög belsejében van, és legyen a PB és AC szakaszok metszéspontja P'. Az értelemszerű jelölésekkel élve, amint azt láttuk, a'g'-b'h'=d'f'-c'e'=0. Azonban most a'<a,g'<g,b'>b és h'>h, vagyis ag-bh>a'g'-b'h'=0. Ugyanígy d'<d,f'<f,c'>c és e'>e miatt df-ce>d'f'-c'e'=0, és így az (ag-bh)(df-ce) szorzat valóban pozitív. Ha pedig a P pont az ABC háromszög belsejében van, akkor hasonló meggondolással azt kapjuk, hogy ag-bh és df-ce is negatív, szorzatuk viszont ebben az esetben is pozitív. Ezzel a bizonyítás végére értünk, az egyenlőség esetét is tisztázva.
