 |
A 2003. novemberi B-jelű matematika feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
B.3672.
Bizonyítandó, hogy minden háromszögből levágható két háromszög úgy, hogy a megmaradó ötszög egy alkalmas pontjából az ötszög minden oldalát hegyesszögben lássuk.(3 pont)
Surányi János (Budapest)
Megoldás: Ha az ABC háromszög (egyik) legnagyobb oldala BC, akkor az A csúcsból induló magasságvonal M talppontja a BC szakasz belső pontja. Az AM szakasz belsejében vegyünk fel egy olyan P pontot, amelyre az MPB és az MPC szög nagysága egyaránt nagyobb, mint \(\displaystyle \pi\)/5, ez elérhető, ha P-t az M ponthoz elég közel választjuk. Legyen K a BM szakasz azon belső pontja, amelyre az MPK szög nagysága \(\displaystyle \pi\)/5. Hasonlóképpen, legyen L a CM szakasz azon belső pontja, amelyre az MPL szög nagysága \(\displaystyle \pi\)/5. Legyen végül E és F az AB illetve AC oldal azon pontja, amelyre az APE és APF szögek nagysága 2\(\displaystyle \pi\)/5. Ekkor az AEKLF ötszög mindegyik oldala 2\(\displaystyle \pi\)/5 szög alatt látszik az ötszög belsejében lévő P pontból. Az ABC háromszögből tehát a BEK és CFL háromszögeket levágva megfelelő ötszöget kapunk.
B.3673.
Oldjuk meg az alábbi egyenletrendszert a pozitív valós számok körében:x2+y2+xy =7, x2+z2+xz =13, y2+z2+yz =19.
(4 pont)
Megoldás: A második egyenletből az elsőt kivonva z2-y2+xz-xy=6, majd a baloldal szorzattá alakítása után (z-y)(x+y+z)=6 adódik. Hasonlóképpen kapjuk a második és harmadik egyenletből, hogy (y-x)(x+y+x)=6. A két eredményt összevetve látható, hogy z-y=y-x, ahonnan x+y+z=3y. Ennélfogva (y-x)3y=6, vagyis xy=y2-2. Ezt az első egyenletbe behelyettesítve kapjuk, hogy x2=9-2y2, amit az x2y2=(y2-2)2 összefüggésbe behelyettesítve Y=y2-re a (9-2Y)Y=(Y-2)2 másodfokú egyenlethez jutunk. Az átalakítás után kapott 3Y2-13Y+4=0 egyenletet megoldva látjuk hogy Y két lehetséges értéke Y=4 és Y=1/3. Figyelembe véve azt is, hogy y pozitív, y lehetséges értékeire y=2, illetve \(\displaystyle y=1/\sqrt{3}\) adódik. Ha y=2, akkor xy=y2-2 miatt x=1, z-y=y-x alapján pedig z=3 adódik, és ez valóban megoldása az egyenletrendszernek. Ha azonban \(\displaystyle y=1/\sqrt{3}\), akkor xy=y2-2<0 miatt x<0 adódna, ebben az esetben tehát nem kapunk megoldást.
B.3674.
Milyen k pozitív egész szám esetén lehet az első k darab prímszám szorzata két pozitív köbszám összege?(4 pont)
Megoldás: Ha k=1, akkor ez lehetséges: 2=13+13. Megmutatjuk, hogy k\(\displaystyle \ge\)2 esetén ez már nem lehetséges. Valóban, ekkor az első k prímszám szorzata osztható 3-mal, 9-cel azonban nem. Ezzel ellentétben, két köbszám összege, ha 3-mal osztható, akkor osztható 9-cel is. Ennek igazolásához vizsgáljuk meg, milyen maradékot adhat egy n egész szám köbe 9-cel osztva. Ha n osztható 3-mal, akkor n3 osztható 9-cel. Minden más esetben n felírható 3k+1 vagy 3k-1 alakban, alkalmas k egész számmal. Mivel
(3k\(\displaystyle \pm\)1)3=27k3\(\displaystyle \pm\)27k2+9k\(\displaystyle \pm\)1=9(3k3\(\displaystyle \pm\)3k2+k)\(\displaystyle \pm\)1,
két egész szám köbének összege pontosan akkor osztható 3-mal, ha vagy mindkét szám osztható 3-mal, vagy pedig közülük 3-mal osztva az egyik +1, míg a másik -1 maradékot ad. Az elmondottak alapján a két egész szám köbének összege mindkét esetben osztható 9-cel.
B.3675.
Egy háromszöget a súlyvonalai hat háromszögre osztanak. Lehet-e ezek közül valamelyik hasonló az eredeti háromszöghöz?(3 pont)
Bártfai Pál (Budapest)
Megoldás: Legyen S a háromszög súlypontja, F az AB oldal felezőpontja. Tegyük fel, hogy az AFS háromszög hasonló az eredeti háromszöghöz. Ha ennek a háromszögnek az A,F,S csúcsoknál lévő szögeit rendre \(\displaystyle \varphi\), \(\displaystyle \psi\), \(\displaystyle \omega\) jelöli, akkor a szokásos jelöléseket használva \(\displaystyle \varphi\)<\(\displaystyle \alpha\), \(\displaystyle \psi\)>\(\displaystyle \beta\) és \(\displaystyle \omega\)>\(\displaystyle \gamma\), így csak két eset lehetséges: vagy \(\displaystyle \varphi\)=\(\displaystyle \beta\), \(\displaystyle \psi\)=\(\displaystyle \gamma\) és \(\displaystyle \omega\)=\(\displaystyle \alpha\), vagy pedig \(\displaystyle \varphi\)=\(\displaystyle \gamma\), \(\displaystyle \psi\)=\(\displaystyle \alpha\) és \(\displaystyle \omega\)=\(\displaystyle \beta\). Tekintsük a második esetet, ekkor a CAF egyenlő szárú háromszögből b=CF. Ez éppen a háromszög c oldalhoz tartozó sc súlyvonala, melyre sc2=(2a2+2b2-c2)/4, ahonnan 4b2=2a2+2b2-c2, vagyis 2a2=2b2+c2. Az AC:AB=AF:FS arányosság alapján kapjuk, hogy b:c=(c/2):(sc/3)=(c/2):(b/3), ahonnan 2b2=3c2. Innen 2a2=3c2+c2, a2=2c2 adódik. Ha tehát az a oldal hosszát a=2-nek választjuk, akkor \(\displaystyle c=\sqrt{2}\) és innen \(\displaystyle b=\sqrt{3}\).
Ez jó is lesz: ha az ABC háromszögben a=2, \(\displaystyle b=\sqrt{3}\) és \(\displaystyle c=\sqrt{2}\), akkor sc2=(2a2+2b2-c2)/4=3, ahonnan \(\displaystyle SF=(1/3)s_c=1/\sqrt{3}\), valamint sa2=(2b2+2c2-a2)/4=3/2, ahonnan \(\displaystyle AS=(2/3)s_a=\sqrt{2}/\sqrt{3}\). Mivel \(\displaystyle AF=(1/2)c=1/\sqrt{2}\), kapjuk hogy
\(\displaystyle BC:CA:AB=a:b:c=2:\sqrt{3}:\sqrt{2}={\sqrt{2}\over\sqrt{3}}: {1\over\sqrt{2}}:{1\over\sqrt{3}}=SA:AF:FS,\)
vagyis az FSA háromszög valóban hasonló az ABC háromszöghöz. A feladatban feltett kérdésre tehát igenlő választ adhatunk.
B.3676.
Bergengóciában a totón négy mérkőzésre lehet tippelni. Betli Benő - nevéhez méltó módon - szeretne barátai előtt egy olyan szelvénnyel büszkélkedni, amelyen egyetlen találat sincs. Hány szelvény ügyes kitöltésével mehet biztosra?(5 pont)
Dobos Sándor (Budapest)
Megoldás: Vizsgáljuk először azt a játékot - hívjuk ezt kettes totónak -, amikor csak az első két mérkőzés eredményére lehet tippelni. Nyilvánvaló, hogy itt 2 szelvény kitöltése még nem elegendő, hiszen ha az első szelvényről az első tipp eredménye, a második szelvényről pedig a második tipp eredménye bejön, akkor nem lesz Benőnek betlis szelvénye. 3 szelvény kitöltése is csak akkor lehet megfelelő, ha a 3 szelvény mindegyike más tippet tartalmaz mind a két mérkőzés eredményére. Ha ugyanis az első két szelvény ugyanazt a tippet (jelöljük ezt A-val) tartalmazza mondjuk az első meccs eredményére, a harmadik szelvényen pedig a másik mérkőzésre a B tipp van megjelölve, akkor Benőnek nem lesz betlis szelvénye abban az esetben, amikor az első mérkőzés kimenetele A, a másodiké pedig B. Ha viszont Benő 3 szelvényt úgy tölt ki, hogy mind a három más tippet tartalmaz az egyes mérkőzések eredményére, akkor ezzel biztosra mehet: akármi is az első mérkőzés eredménye, két olyan szelvénye lesz, amelyiken arra rosszul tippelt, és ezek közül legalább az egyiken rossz tipp szerepel a második meccs kimenetelére is.
Vizsgáljuk meg most a hármas totó esetét, amikor is az első három mérkőzésre lehet tippelni. Ha Benő csak 4 szelvényt tölt ki, akkor valamelyik mérkőzésre két szelvényen is ugyanazt kell, hogy megjelölje, és ha ez a találat éppen bejön, akkor Benő szelvényei között már csak legfeljebb 2 alkalmas szelvény marad, ami, mint láttuk, nem elég arra, hogy Benő teljes bizonyossággal az első két mérkőzés eredményének egyikét se találja el. Nyilván ennél kevesebb szelvény kitöltése még inkább nem elegendő. 5 szelvény kitöltésével viszont már biztosra mehet, ha a következő séma alapján jár el: AAA, BBA, ABC, BAC, CCB. Itt A,B,C az 1,2,X tetszőleges permutációját jelenti. Valóban, ha a harmadik meccs eredménye A, akkor a harmadik, negyedik és ötödik szelvény jöhet szóba; mivel ezeken az első két mérkőzésre rendre az AB, BA, CC tippek szerepelnek, a kettes totóra vonatkozó megjegyzésünk alapján e három szelvény közül valamelyik biztosan nem tartalmaz egyetlen találatot sem. Hasonló a helyzet akkor is, ha a harmadik mérkőzés eredménye C. Végül, ha a harmadik meccs eredménye B, akkor az első négy szelvény jöhet szóba, és akármi is az első mérkőzés kimenetele, ezek közül még mindig marad kettő, ami ezt nem találja el, és különböző tippet tartalmaz a második meccsre.
Rátérve az eredeti kérdésre, 7 szelvény kitöltésével Benő még nem mehet biztosra (és akkor persze 7-nél kevesebb szelvény kitöltése sem lehet elegendő). Ha ugyanis Benő 7 szelvényt tölt ki, akkor lesz közöttük legalább 3 olyan, amelyiken a negyedik mérkőzés eredményére ugyanaz a tipp szerepel. Ha a negyedik mérkőzésnek éppen ez lesz az eredménye, akkor Benő szelvényei között már csak legfeljebb 4 olyan marad, amely a célnak esetleg megfelelhet. Ezek valamelyike kell hogy rossz tippet tartalmazzon az első 3 meccs mindegyikére. Azt viszont már láttuk, hogy a hármas totó esetében Benőnek legalább 5 szelvényt ki kell töltenie.
Azonban 8 szelvény kitöltésével már elérheti célját, ha azokat így tölti ki: 1111, 2211, XX21, 2222, 1122, XX12, 12XX, 21XX. Valóban, ha az utolsó meccs eredménye 1, akkor az utolsó 5 szelvény jöhet szóba, melyeken az első három mérkőzésre rendre a 222, 112, XX1, 12X, 21X tippek szerepelnek, ami megfelel az első sémának az A=2, B=1, C=X választással. Mivel az 1 és 2 jelölések felcserélésével ugyanezt a 8 szelvényt kapjuk, hasonló a helyzet akkor is, ha az utolsó meccs eredménye 2. Végül, ha az utolsó meccs eredménye X, akkor az első 6 szelvény valamelyikén kell elérni, hogy az első három mérkőzés egyikére se legyen találat. Ebben az esetben, ha a harmadik mérkőzés eredménye 1 vagy X, akkor elég a harmadik, negyedik és ötödik szelvény valamelyikén elérni, hogy az első két mérkőzés egyikére se legyen találat, ez pedig elérhető, hiszen ezeken a szelvényeken az első két meccsre rendre az XX, 22, 11 tippek szerepelnek. Szimmetria okokból hasonló a helyzet akkor is, ha a harmadik mérkőzés eredménye 2, csak most az első, második és hatodik szelvényt kell megnézni.
B.3677.
Határozzuk meg mindazokat a pozitív egészekből álló (\(\displaystyle \alpha\);\(\displaystyle \beta\)) számpárokat, amelyekre a pozitív egészek halmazát fel lehet bontani két diszjunkt halmazra, A-ra és B-re úgy, hogy {\(\displaystyle \alpha\)a | a\(\displaystyle \in\)A}= {\(\displaystyle \beta\)b | b\(\displaystyle \in\)B} teljesüljön.(4 pont)
IMC10, Kolozsvár, 2003
Megoldás: Tegyük fel, hogy létezik ilyen felbontás, ekkor vagy 1\(\displaystyle \in\)A vagy 1\(\displaystyle \in\)B tejesül. Az első esetben
\(\displaystyle \alpha\) {
{  a | a
a | a A}={
A}={  b | b
b | b B}
B}
miatt van olyan b B, amelyre
B, amelyre  =
= b, vagyis
b, vagyis  osztója
osztója  -nak. A második esetben hasonló módon következik, hogy
-nak. A második esetben hasonló módon következik, hogy  osztja
osztja  -t. A kívánt felbontás tehát csak akkor lehetséges, ha az
-t. A kívánt felbontás tehát csak akkor lehetséges, ha az  és
és  számok közül valamelyik osztja a másikat. Ha történetesen
számok közül valamelyik osztja a másikat. Ha történetesen  =
= , akkor a feladatban szereplő két halmaz egyenlőségéből A=B adódik, ekkor tehát nem létezik a kívánt felbontás.
, akkor a feladatban szereplő két halmaz egyenlőségéből A=B adódik, ekkor tehát nem létezik a kívánt felbontás.
Most megmutatjuk, hogy ha  =d
=d , ahol d egynél nagyobb egész szám, akkor a keresett felbontás megvalósítható. Jelölje T azon pozitív egészek halmazát, amelyek d-vel nem oszthatók, és minden k nemnegatív egész számra definiáljuk a Tk={ dkt | t
, ahol d egynél nagyobb egész szám, akkor a keresett felbontás megvalósítható. Jelölje T azon pozitív egészek halmazát, amelyek d-vel nem oszthatók, és minden k nemnegatív egész számra definiáljuk a Tk={ dkt | t T} halmazt. Ekkor a Tk halmazok páronként diszjunktak, egyesítésük pedig éppen a pozitív egész számok halmaza lesz. Legyen A=T0
T} halmazt. Ekkor a Tk halmazok páronként diszjunktak, egyesítésük pedig éppen a pozitív egész számok halmaza lesz. Legyen A=T0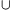 T2
T2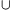 T4
T4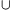 ... a páros indexű Ti halmazok egyesítése, B=T1
... a páros indexű Ti halmazok egyesítése, B=T1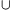 T3
T3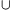 T5
T5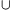 ... pedig a páratlan indexű Ti halmazok egyesítése; ekkor nyilván A és B diszjunkt halmazok, egyesítésük pedig a pozitív egészek halmaza. Ha n=
... pedig a páratlan indexű Ti halmazok egyesítése; ekkor nyilván A és B diszjunkt halmazok, egyesítésük pedig a pozitív egészek halmaza. Ha n= a valamilyen a
a valamilyen a A számra, akkor létezik olyan k nemnegatív egész és t
A számra, akkor létezik olyan k nemnegatív egész és t T, hogy a=d2kt, mely esetben n=(d
T, hogy a=d2kt, mely esetben n=(d )(d2kt)=
)(d2kt)= b, ahol b=d2k+1t eleme T2k+1-nek, és ezáltal B-nek is. Következésképpen
b, ahol b=d2k+1t eleme T2k+1-nek, és ezáltal B-nek is. Következésképpen 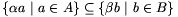 . Fordítva, ha n=
. Fordítva, ha n= b teljesül valamilyen b
b teljesül valamilyen b B számra, akkor létezik olyan k nemnegatív egész és t
B számra, akkor létezik olyan k nemnegatív egész és t T, hogy b=d2k+1t, mely esetben n=(
T, hogy b=d2k+1t, mely esetben n=( /d)(d2k+1t)=
/d)(d2k+1t)= a, ahol a=d2kt eleme T2k-nak, és ezáltal A-nak is, ami igazolja, hogy
a, ahol a=d2kt eleme T2k-nak, és ezáltal A-nak is, ami igazolja, hogy 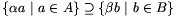 , tehát {
, tehát {  a | a
a | a A}={
A}={  b | b
b | b B}.
B}.
Szimmetria okokból, a keresett felbontás megvalósítható akkor is, ha  =d
=d  alkalmas egynél nagyobb d egész számmal. Összefoglalva, a keresett számpárok pontosan azok az (
alkalmas egynél nagyobb d egész számmal. Összefoglalva, a keresett számpárok pontosan azok az ( ,
, ) párok, ahol
) párok, ahol  és
és  különböző pozitív egész számok, és közülük valamelyik egész számú többszöröse a másiknak.
különböző pozitív egész számok, és közülük valamelyik egész számú többszöröse a másiknak.
B.3678.
A konvex ABCD négyszög A csúcsán át a BD átlóval és B csúcsán át az AC átlóval párhuzamosan húzott egyenesek metszéspontja E. Bizonyítsuk be, hogy az EC egyenes ugyanolyan arányban osztja a BD átlót, mint az ED egyenes az AC átlót.(3 pont)
Surányi János (Budapest)
Megoldás: Jelölje az átlók metszéspontját M, az AM és ED szakaszok metszéspontját Y, a BM és EC szakaszok metszéspontját pedig X. Ekkor az AMBE négyszög parallelogramma, amelyben EB=AM és AE=MB. Az EBX és CMX háromszögek hasonlóságából adódóan
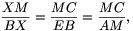
ahonnan
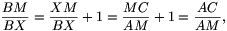
vagyis
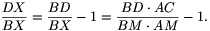
Szimmetria okok miatt a CY/AY arányt megkapjuk, ha a fenti kifejezésben az A és B, illetve a C és D pontok szerepét felcseréljük. Mivel a kifejezés ezáltal nem változik, kapjuk, hogy CY/AY=DX/BX, éppen amit bizonyítanunk kellett.
B.3679.
Bizonyítsuk be, hogy tetszőleges a, b, c, d pozitív számokra: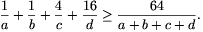
(4 pont)
Megoldás: Ha x,y pozitív számok, akkor (x-y)2 0 miatt (x+y)2=(x-y)2+4xy
0 miatt (x+y)2=(x-y)2+4xy 4xy, ahol egyenlőség az x=y esetben áll fenn. Az egyenlőtlenséget a pozitív xy(x+y) mennyiséggel leosztva kapjuk hogy
4xy, ahol egyenlőség az x=y esetben áll fenn. Az egyenlőtlenséget a pozitív xy(x+y) mennyiséggel leosztva kapjuk hogy
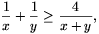
ahol egyenlőség pontosan az x=y esetben áll fenn. Ezen egyenlőtlenség ismételt alkalmazásával nyerjük a bizonyítanó állítást:
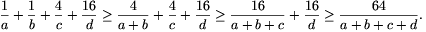
Egyenlőség pontosan akkor áll fenn, ha az mindhárom közbülső esetben teljesül, vagyis a=b, a+b=c, a+b+c=d esetén, ami azzal ekvivalens, hogy a=b=t, c=2t, d=4t alkalmas pozitív t számmal.
B.3680.
A hegyesszögű ABC háromszög körülírt köréhez érintőket húzunk az A, B és C csúcsokban. Tekintsük azt a PQR háromszöget, amelynek ezek az érintők az oldalai, a betűzést úgy választva, hogy C a PQ oldalon helyezkedjék el, B a PR oldalon, végül az A a QR oldalon.Jelölje C1 az ABC háromszög C-ből induló magasságának a talppontját az AB oldalon. Bizonyítsuk be, hogy CC1 felezi a QC1P szöget.
(5 pont)
Gillis-Turán verseny
Megoldás: A szokásos jelöléseket használva a CC1B derékszögű háromszögből CC1=asin  és C1B=acos
és C1B=acos  . A kerületi és középponti szögek tételének alapján a BCP egyenlő szárú háromszög P-nél lévő csúcsszöge
. A kerületi és középponti szögek tételének alapján a BCP egyenlő szárú háromszög P-nél lévő csúcsszöge  -2
-2 , vagyis a BCP és CBP szög egyaránt
, vagyis a BCP és CBP szög egyaránt  . Ezért CP=BP=a/(2cos
. Ezért CP=BP=a/(2cos  ). A C1BP háromszögre a koszinusz-tételt felírva
). A C1BP háromszögre a koszinusz-tételt felírva
C1P2=C1B2+BP2-2C1B.BP.cos ( +
+ )=
)=
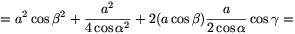
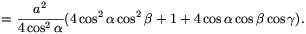
Szimmetria okokból CQ=b/(2cos  ) és
) és
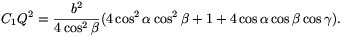
Ezért
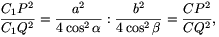
vagyis C1P:C1Q=CP:CQ. A szögfelező-tétel megfordítása miatt tehát a PQC1 háromszög C1-ből induló szögfelezője a PQ oldalt a C pontban metszi, és éppen ezt kellett bizonyítanunk.
B.3681.
Egy tetraéder hat éle közül ötnek a hosszáról tudjuk, hogy nem nagyobb, mint 2. Igazoljuk, hogy a tetraéder térfogata legfeljebb 1.(4 pont)
Megoldás: Tegyük fel, hogy az ABCD tetraéderben a CD él kivételével minden él hosszáról tudjuk, hogy nem nagyobb 2-nél. Legyen az AB él hossza 2x, ahol tehát x 1. Ha a C pont vetülete az AB egyenesre M, akkor az AM és BM szakaszok közül valamelyik hossza legalább x, és így a Pithagorasz tétel alapján MC2
1. Ha a C pont vetülete az AB egyenesre M, akkor az AM és BM szakaszok közül valamelyik hossza legalább x, és így a Pithagorasz tétel alapján MC2 4-x2. Az ABC háromszög AB oldalhoz tartozó magassága tehát nem hosszabb, mint
4-x2. Az ABC háromszög AB oldalhoz tartozó magassága tehát nem hosszabb, mint 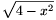 , és ugyanez igaz az ABD háromszög AB oldalhoz tartozó magasságára is. Mivel ez utóbbi nem lehet nagyobb a tetraéder ABC lapjához tartozó magasságánál, a tetraéder térfogata nem lehet nagyobb, mint
, és ugyanez igaz az ABD háromszög AB oldalhoz tartozó magasságára is. Mivel ez utóbbi nem lehet nagyobb a tetraéder ABC lapjához tartozó magasságánál, a tetraéder térfogata nem lehet nagyobb, mint
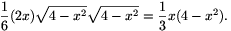
Elegendő tehát azt megmutatni, hogy 0<x 1 esetén x(4-x2)
1 esetén x(4-x2) 3, vagyis hogy
3, vagyis hogy
x3-4x+3=(x-1)(x2+x-3) 0.
0.
Ez pedig nyilván igaz, hiszen a megengedett tartományban x-1 0 és x2+x-3
0 és x2+x-3 -1<0. Az is leolvasható a bizonyításból, hogy a tetraéder térfogata csakis akkor lehet 1, ha x=1, az ABC és ABD háromszögek AB oldalhoz tartozó magassága egyaránt
-1<0. Az is leolvasható a bizonyításból, hogy a tetraéder térfogata csakis akkor lehet 1, ha x=1, az ABC és ABD háromszögek AB oldalhoz tartozó magassága egyaránt 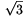 , továbbá a tetraéder ABC laphoz tartozó magassága egybeesik az ABD háromszög AB oldalhoz tartozó magasságával. Ez pontosan azt jelenti, hogy mind az ABC, mind az ABD lap 2 egység oldalú szabályos háromszög, melyek síkja egymásra merőleges.
, továbbá a tetraéder ABC laphoz tartozó magassága egybeesik az ABD háromszög AB oldalhoz tartozó magasságával. Ez pontosan azt jelenti, hogy mind az ABC, mind az ABD lap 2 egység oldalú szabályos háromszög, melyek síkja egymásra merőleges.
