 |
A C. 1302. feladat (2015. szeptember) |
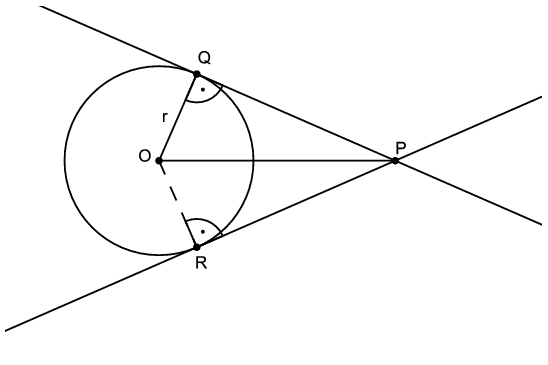
C. 1302. Adott egy \(\displaystyle O\) középpontú, \(\displaystyle r\) sugarú kör, és rajta kívül egy \(\displaystyle P\) pont. A \(\displaystyle P\)-ből húzott érintők érintési pontjai a körön legyenek \(\displaystyle Q\) és \(\displaystyle R\). Mekkora legyen az \(\displaystyle |OP|\) távolság, hogy a \(\displaystyle PQOR\) négyszög területe megegyezzen a kör területével?
(5 pont)
A beküldési határidő 2015. október 12-én LEJÁRT.
Megoldás. Készítsünk ábrát. Mivel egy körhöz húzott érintő merőleges az érintési pontba húzott sugárra, így \(\displaystyle PQO\sphericalangle=PRO\sphericalangle=90^{\circ}\).
Az \(\displaystyle OPQ\) derékszögű háromszögben Pitagorasz tételét felírva: \(\displaystyle QP^2=OP^2-r^2\). Ennek a háromszögnek a területe: \(\displaystyle t_{PQO}=\frac12\cdot QP\cdot QO=\frac12r\cdot QP\).
A kör területe: \(\displaystyle t_{\circ}=r^2\pi\). Mivel az \(\displaystyle OPQ\) és az \(\displaystyle OPR\) háromszög egybevágó (két oldal és a nagyobbikkal szemközti szög megegyezik), ezért \(\displaystyle t_{PQOR}=t_{PQO}+t_{PRO}=2t_{PQO}=2\cdot \frac12r\cdot QP=r\cdot QP\).
A feltétel szerint tehát \(\displaystyle r^2\pi=r\cdot QP\), vagyis (\(\displaystyle r>0\)-val osztva mindkét oldalt) \(\displaystyle r\pi=QP\), amiből \(\displaystyle r^2\pi^2=QP^2=OP^2-r^2\). Innen \(\displaystyle r^2\pi^2+r^2=OP^2\), vagyis \(\displaystyle r^2(\pi^2+1)=OP^2\), amiből \(\displaystyle OP=r\sqrt{\pi^2+1}\). Mivel \(\displaystyle r\), \(\displaystyle \pi\), \(\displaystyle QP\) és \(\displaystyle OP\) pozitív, ezért a gondolatmenet visszafelé is igaz, tehát ha \(\displaystyle |OP|=r\sqrt{\pi^2+1}\), akkor a \(\displaystyle PQOR\) négyszög területe megegyezik a kör területével.
Statisztika:
A KöMaL 2015. szeptemberi matematika feladatai

