A C. 1303. feladat (2015. szeptember)

C. 1303. Egy \(\displaystyle 130~\rm{cm}^2\) területű, téglalap alakú origami papír két szomszédos csúcsát szimmetrikusan középre hajtottuk úgy, hogy a középre hajtott két oldal szabályos háromszöget formáz az ábra szerint. Mekkorák az eredeti papírlap oldalai?

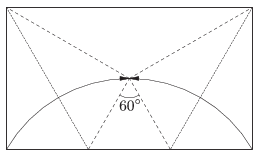
(5 pont)

A beküldési határidő 2015. október 12-én LEJÁRT.

Megoldás. A hajtás miatt a megfelelő szögek és szakaszok megegyeznek, ezt jelöljük az ábrán.

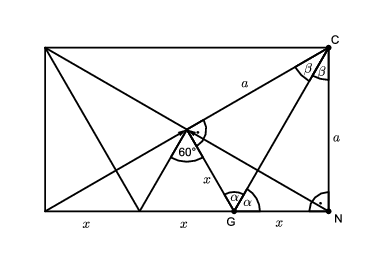
A \(\displaystyle G\) csúcsnál \(\displaystyle 180^{\circ}=60^{\circ}+2\alpha\), amiből \(\displaystyle \alpha=60^{\circ}\). A \(\displaystyle CNG\) derészögű háromszögben \(\displaystyle \beta=GCN\sphericalangle=180^{\circ}- 90^{\circ}-60^{\circ}=30^{\circ}\), vagyis a \(\displaystyle CNG\) háromszög egy szabályos háromszög fele, és így \(\displaystyle GC=2x\). Felírva a háromszögre a Pitagorasz-tételt: \(\displaystyle a^2=(2x)^2-x^2=3x^2\), amiből \(\displaystyle a=\sqrt3x\).

A téglalap területe \(\displaystyle 3x\cdot a\), vagyis \(\displaystyle 130=3x\cdot\sqrt3 x\), ahonnan \(\displaystyle x^2=\frac{130}{3\sqrt3}\), vagyis \(\displaystyle x=\sqrt{\frac{130}{3\sqrt3}}\).

A téglalap oldalai: \(\displaystyle 3x=3\sqrt{\frac{130}{3\sqrt3}}\) és \(\displaystyle a=\sqrt3x=\sqrt{\frac{130}{\sqrt3}}\).

Statisztika:

338 dolgozat érkezett.
5 pontot kapott:	259 versenyző.
4 pontot kapott:	53 versenyző.
3 pontot kapott:	12 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	5 dolgozat.

A KöMaL 2015. szeptemberi matematika feladatai