KöMaL Problems in Mathematics, December 2005
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on January 10, 2006. |
K. 61. There is a 20 by 10-metre rectangular park next to one of the chateaux on the Loire. A rectangular spiral path of 1 metre width leads to the interior of the park. The lord of the chateau walks down the spiral path every morning (always staying in the middle of the path and making right-angle turns at the corners), waters the white daisies he grows in a square flowerbed 1 m on a side, and then he walks back. What is the distance he covers altogether?
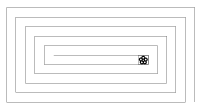
(6 pont)
solution (in Hungarian), statistics
K. 62. Sophie has a toy that contains 9 wooden rods of different colours sticking out of a square wooden board, as shown in the figure. It is a logical puzzle. The task is to place nine red, nine green, and nine blue rings of the same shape on the rods. Each rod should have three rings of different colours on it, and at each level, the colours of the three rings along the directions indicated by the arrows in the diagram should also be different. In how many arrangements can the rings be placed on the rods? (Two arrangements count as different if there is at least one rod on which the order of the rings is different.)
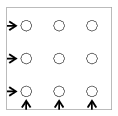
(6 pont)
solution (in Hungarian), statistics
K. 63. In the triangle ABC, X is the midpoint of side AB and Y is the midpoint of side AC. BY and CX intersect at S. Show that a) the areas of the triangles SBX and SCY are equal; b) the areas of triangle SBC and quadrilateral AXSY are equal.
(6 pont)
solution (in Hungarian), statistics
K. 64. Express the following sum as a ratio of two integers:
(6 pont)
solution (in Hungarian), statistics
K. 65. x is a real number, such that . Determine the exact values of
and
.
(6 pont)
solution (in Hungarian), statistics
K. 66. There are only 5 candies left on the Christmas tree: two of them filled with jelly and the other three filled with almond paste. The wrapping of the candies does not show the flavour. Hanga decided to eat one of them every day. Which is more probable: that she will eat the second jelly-filled candy on the third day, or that she will eat the third almond paste candy on the fourth day?
(6 pont)
 |
Problems with sign 'C'Deadline expired on January 16, 2006. |
C. 830. Lord Moneybag said to his grandson, ``Listen, Bill. Christmas is coming up. I have got some money between 300 and 500 pounds on me. It is an integer multiple of 6 pounds. I will give you 5 pounds out of it in one-pound coins. As I hand you the coins one by one, the amount that remains on me will first be divisible by 5, then by 4, then by 3, then by 2 and finally only by 1. If you can tell me how many pounds I have got on me, you'll get an extra ten-pound note.'' How much money did the lord have on him?
(5 pont)
solution (in Hungarian), statistics
C. 831. Find the sum of all three-digit numbers whose digits are all odd.
(5 pont)
solution (in Hungarian), statistics
C. 832. Given are the points A(2,1), B(3,4), C(2,11) on the cartesian plane, show that the ray OB bisects the angle AOC.
(5 pont)
solution (in Hungarian), statistics
C. 833. The base edges and the height of a square-based right pyramid are all 40 cm long. We want to connect one vertex of the base to the opposite vertex of the base with a line drawn on the lateral faces. What is the length of the shortest path?
(5 pont)
solution (in Hungarian), statistics
C. 834. Solve the following equation:
(5 pont)
 |
Problems with sign 'B'Deadline expired on January 16, 2006. |
B. 3862. In how many different ways is it possible to place 32 knights on a 8×8 chessboard, such that no pair of them should attack each other?
(4 pont)
solution (in Hungarian), statistics
B. 3863. Show that the number
is divisible by 1003. Is it also divisible by 2006?
(3 pont)
solution (in Hungarian), statistics
B. 3864. ABCD is a cyclic quadrilateral, and AC=BC. The perpendicular projections of the point C onto the lines AD and BD are E and F, respectively. Show that AE=BF.
(3 pont)
solution (in Hungarian), statistics
B. 3865. The triangles AB1C1 and AB2C2 are similar, and their vertices are labelled in the same direction around the triangle. The lines B1B2 and C1C2 intersect at the point D. (a) Show that the triangles AB1B2 and AC1C2 are similar. (b) Show that the circumscribed circles of AB1C1 and AB2C2 pass through the point D.
(4 pont)
solution (in Hungarian), statistics
B. 3866. For which point P of an arc AB of a circle does the triangle ABP have the longest perimeter?
(4 pont)
solution (in Hungarian), statistics
B. 3867. Let n denote a positive integer, such that 4n+2n+1 is a prime number. Prove that n is an integer power of 3.
(5 pont)
solution (in Hungarian), statistics
B. 3868. It is well known that cos 2x can be expressed as a polynomial of cos x: cos 2x=2cos2x-1. Is it possible to express sin 2x as a polynomial of sin x?
(4 pont)
solution (in Hungarian), statistics
B. 3869. Point M lies on the angle bisector drawn from vertex A, inside an acute-angled triangle ABC. The other intersections of the lines AM, BM, CM with the circumscribed circle are A1, B1 and C1, respectively. The lines AB and C1A1 intersect at L, and the lines AC and B1A1 intersect at N. Prove that LN is parallel to BC.
(5 pont)
solution (in Hungarian), statistics
B. 3870. P is a point lying on an ellipse of foci F1 and F2, different from the endpoints of the major axis. Show that the value of
is independent of P.
(4 pont)
solution (in Hungarian), statistics
B. 3871. Solve the equation
x2-x-1=2x-log2(x2+2x)
on the set of positive numbers.
(5 pont)
 |
Problems with sign 'A'Deadline expired on January 16, 2006. |
A. 386. Consider one of the two arcs of a rectangular hyperbola centred at O, and choose an arbitrary point P on it. Let Q and R denote the intersections of the hyperbola and the circle of radius 2OP drawn about P. Prove that  QPR=120o.
QPR=120o.
(5 pont)
A. 387. We have n marbles that look all alike, but we know that one of them is radioactive. We want to find that marble. We also have a detector that can determine whether any chosen subset of the marbles contains the radioactive marble or not. We want to choose a measurement strategy for which the expected number of measurements is a minimum. Find that smallest expected value possible.
(5 pont)
A. 388. In the hexagon ABCDEF we have AB=BC, CD=DE and EF=FA. Prove that
(5 pont)
Upload your solutions above.
