A KöMaL 2007. januári informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2007. február 15-én LEJÁRT. |
I. 148. Egy osztály minden tanulója karácsonyra osztálytársainak különféle ajándékokkal kedveskedik. Mivel nem akarják, hogy bárki is irigykedjen a másikra, ezért a következő módon végzik az ajándékozást: minden tanuló készít annyi egyforma ajándékcsomagot, ahány osztálytársa van, majd a csomagokra ráírja egy-egy osztálytársa nevét, senkit sem hagy ki. Ezután a csomagokat a karácsonyfa alá rakja. Egy ajándékcsomagban többféle ajándékból egy, vagy több lehet, de legalább az egyik féléből van egy. Természetesen önmagát nem ajándékozza meg senki. (Például Aladár mindenkinek csokit és kisautót ad, Béla könyvet és tollat, Cecil egy csokit és egy könyvet stb.)
Ajándékozás után szeretnék kitalálni, hogy ki milyen ajándékokkal lepte meg társait. Ezért ajándékaikról listát készítenek, melyeket egy táblázatkezelő egy munkalapján foglalnak össze. Készítsünk olyan táblázatot, amely egy másik munkalapra kiszámítja minden tanulóra, hogy milyen ajándékokat adott a többieknek.
A táblázat első munkalapja első sorának első két cellájában található a tanulók N száma (1<N<40), és a különböző ajándékok M száma (1<M<100). A munkalapon a második sortól kezdődően minden sor celláiba le van írva, hogy az adott sornak megfelelő tanuló hány darabot kapott az adott oszlopnak megfelelő ajándékból. A megoldásban a másik munkalapon az előbbi táblázathoz hasonló formában az szerepeljen, hogy hány darabot adott egy társának az adott oszlopnak megfelelő ajándékból az adott sornak megfelelő tanuló. Az érvénytelen cellákban ne látszódjon semmi.
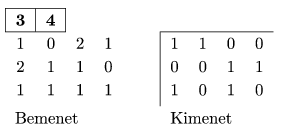
Beküldendő a táblázat (i148.xls, ...).
(10 pont)
I. 149. Készítsünk prezentációt, amely bemutatja az Európai Unió országait és az EU fejlődését az 1993. novemberi Maastrichti Szerződéstől a 2007. januári bővítésig. A prezentáció alapja egy Európát ábrázoló fekete--fehér vaktérkép legyen, melyen csak az országhatárok látszanak. A prezentáció egyes fázisaiban színezzük ki egyesével az alapító, illetve belépő államokat, jelenítsük meg az ország és a főváros nevét, a belépés időpontját. Az alapító 12 országot sötétkék, az első bővítésben belépő országokat kék, a 2007. elején belépőket világoskék színnel fessük be.
Beküldendő a bemutató (I149.ppt, ...).
(10 pont)
I. 150. Egy közlekedési lámpánál N darab (néhány száz) jármű gyűlt össze. A lámpa működési ciklusa alapján 45 másodperc zöld után 15 másodpercig pirosat jelez. Készítsünk programot, amely grafikusan ábrázolja a gépkocsik áthaladását. A járműveket téglalapokként ábrázoljuk, melyeknek szélessége legyen állandó, a hosszuk pedig véletlenszerű. A jármű gyorsulása fordítottan arányos a hosszával. A legrövidebb jármű 2 méteres, és 4 másodperc alatt éri el a 100 km/h sebességet, a leghosszabb 20 méteres, és 1 perc alatt éri el ezt a sebességet. Az első autó a zöld jelzésre indul és maximális gyorsulással éri el a megengedett legnagyobb sebességet (50 km/h). A mögötte álló 1 másodperc elteltével indul, és vagy ugyanúgy gyorsul, mint az előtte levő, vagy lassabban, a saját paramétereinek megfelelően. Ha egy jármű 20 méternél jobban megközelít egy előtte álló autót, akkor azonnal fékez és pontosan 2 méterrel ez előtte haladó mögött áll meg. Ha a féktávolságon belül kap piros jelzést (20 méter), az autó még áthalad, ha nem, akkor pontosan a lámpa vonalában áll meg. Minden kocsi helyzetét minden másodpercben határozzuk meg, és rajzoljuk ki. A lámpán áthaladó jármű mindig eltűnik a grafikus képernyőről, a mögötte állók pedig fokozatosan tűnnek fel, amíg el nem fogy az előre véletlenszerűen meghatározott sor. A képernyőn a lámpa előtt várakozó kocsik kb. a rendelkezésre álló képterület 80%-át töltsék ki, a túlhaladó járművek a maradék 20% helyen látsszanak.
Beküldendő a megfelelően dokumentált forráskód.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2007. február 15-én LEJÁRT. |
S. 23. Egy egyszerű háttértáron található fájlokat és azok egyes darabjainak elhelyezkedését mutatja az alábbi táblázat:
1. idojaras.txt 160 0
2. --- 17 5
3. mese.doc 180 0
4. --- 20 2
5. --- 5 10
6. mese.doc 28 3
7. hoember 128 0
8. mikulas.jpg 560 0
9. hoember 47 7
10. --- 633 0
A táblázat sorai (legföljebb 100000 sor) a háttértár egymást követő különböző méretű részeit jelentik. Minden sorban elsőként a tárolt állomány neve, vagy három kötőjel szerepel (a sorszámokat csak a könnyebb érthetőség miatt írtuk ki, a táblázatban nem szerepelnek).
A fájlnév az angol abc kisbetűit és esetleg egy pontot tartalmaz, a három kötőjel a háttértár szabad területét jelzi. A fájlnév, illetve ,,---'' után szóközzel elválasztva a fájl, vagy szabad rész adott darabjának méretét adja (1 és 100000 közötti egész), valamint egy szóköz után a következő rész helyét a táblázatban (pozitív egész, illetve zérus, ha ez a fájl, vagy szabad rész vége).
Készítsünk programot, amely megadja a fenti szerkezetű háttértár állományait és szabad területét abc sorrendben. A név után szóközzel elválasztva megjeleníti a fájl teljes méretét, valamint megfelelő sorrendben az állomány által elfoglalt területek kezdetét és végét kötőjellel elválasztva. A fenti példa esetén a kimenet:
hoember 175 1099-1145 411-538
idojaras.txt 160 1-160
mese.doc 208 383-410 178-357
mikulas.jpg 560 539-1098
--- szabad 675 358-377 161-177 378-382 1046-1078
A program a be- és kimeneti fájlok nevét a parancssorból olvassa be, használata például S23.exe bemenet.txt kimenet.txt. A bemeneti állomány a fenti példa szerinti szerkezetű (sorszámok nélkül). A programokat több bemeneti állománnyal is teszteljük, teljes pontszámot csak a több tízezer fájl esetén is néhány perc alatt eredményt adó megoldások kaphatnak.
Beküldendő a megoldást tartalmazó program forrásállománya (S23.pas, S23.cpp, ...), valamint a megoldás rövid dokumentációja (S23.txt, S23.pdf, ...).
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

