KöMaL Problems in Mathematics, April 2011
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'C'Deadline expired on May 10, 2011. |
C. 1075. Find the three-digit number that is twelve times the sum of its digits.
(5 pont)
solution (in Hungarian), statistics
C. 1076. The roots of a quadratic equation are the squares of two consecutive integers. The geometric mean of the two roots is 1 greater than the difference of the roots. Write down the quadratic equation in question.
(5 pont)
solution (in Hungarian), statistics
C. 1077. E is the point dividing side AC of triangle ABC in a 3:1 ratio, such that EC is the shorter part. The line passing through E and the midpoint F of side BC intersects the line AB at D. What percentage is the area of triangle ADE of the triangle ABC?
(5 pont)
solution (in Hungarian), statistics
C. 1078. Define ``words'' as strings of at most ten characters made out of the 26 letters of the English alphabet. (A ``word'' may as well consist of a single letter, and two ``words'' are considered different if they differ in at least one letter.) Prove that the number of all possible ``words'' obtained in this way is divisible by 27.
(5 pont)
solution (in Hungarian), statistics
C. 1079. We have a champagne glass shaped like a truncated cone. The radius of the base circle is 1 cm, the radius of the top circle is 4 cm and its height is 6 cm (see the figure). To what height do we need to fill the glass to have half a glass of drink?
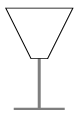
(5 pont)
 |
Problems with sign 'B'Deadline expired on May 10, 2011. |
B. 4352. What is the minimum possible number of convex pentagons needed to put together a convex 2011-sided polygon out of them?
(Suggested by J. Mészáros, Jóka)
(3 pont)
solution (in Hungarian), statistics
B. 4353. Let A be a positive integer, and let B denote the number obtained by writing the digits of A in reverse order. Show that at least one of the numbers A+B and A-B is divisible by 11.
(Suggested by J. Mészáros, Jóka)
(3 pont)
solution (in Hungarian), statistics
B. 4354. Given four distinct points A, B, C, D on the plane, construct two circles touching each other on the outside such that one of them passes through A and B, the other passes through C and D, and their point of tangency lies on the line segment BC.
(4 pont)
solution (in Hungarian), statistics
B. 4355. Prove that if the product of the positive numbers x, y and z is 1, then
(Based on the idea of J. Szoldatics, Dunakeszi)
(4 pont)
solution (in Hungarian), statistics
B. 4356. On the same side of a given line segment AB, there are at most six similar triangles one side of which is AB. Prove that the third vertices of all these triangles are concyclic.
(4 pont)
solution (in Hungarian), statistics
B. 4357. Let n>1 be a positive integer. Show that n3-n2 is a factor of the binomial coefficient .
(Suggested by G. Holló, Budapest)
(3 pont)
solution (in Hungarian), statistics
B. 4358. Solve the following equation: .
(Suggested by B. Kovács, Szatmárnémeti)
(5 pont)
solution (in Hungarian), statistics
B. 4359. A regular tetrahedron is intersected with a plane perpendicular to one of its faces in line e. The lines of intersection of this plane with the other three faces enclose angles of 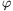 1,
1, 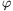 2,
2, 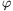 3 with e. Determine the possible values of he expression
3 with e. Determine the possible values of he expression .
(5 pont)
solution (in Hungarian), statistics
B. 4360. Let S(n) denote the sum of the digits for any positive integer n. For what integers k greater than 1 is there a positive real number ck such that S(kn) ck.S(n) for all positive integers n?
ck.S(n) for all positive integers n?
(Suggested by P. Erben, Budapest)
(5 pont)
solution (in Hungarian), statistics
B. 4361. Let a and b denote the semi-axes of an ellipse. Let O denote the centre, and let be points on the curve such that each of the angles PiOPi+1 is
. Prove that if n>1 then
.
(5 pont)
 |
Problems with sign 'A'Deadline expired on May 10, 2011. |
A. 533. Determine all triples (a,b,c) of positive integers for which abc+1 divides a2+b2.
(5 pont)
A. 534. The sides of a triangle are a, b and c, the lengths of the corresponding medians are sa, sb and sc, respectively. Prove that .
(Proposed by: Donát Nagy, Szeged)
(5 pont)
A. 535. There is given a simple graph G with vertices v1,...,vn. H1,...,Hn are sets of nonnegative integers such that for every i=1,2,...,n, the cardinality of Hi is at most half of the degree of vi. Prove that G contains a subgraph G' with the same vertices such that the degree of vi in G' is not an element of Hi for any i.
(Proposed by: László Miklós Lovász, Budapest)
(5 pont)
Upload your solutions above.
