A KöMaL 2014. szeptemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2014. október 10-én LEJÁRT. |
M. 343. Mérjük meg valamely két fonállal ,,bifilárisan'' felfüggesztett, 5 dkg-os nehezékkel ellátott fonálinga lengésének csillapodását! Az ingát vízszintesen kitérített helyzetéből engedjük el. Mérjük és ábrázoljuk az inga lengésidejét és maximális kilendülési szögét a lengések számának függvényében!
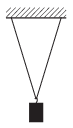
Mikola Sándor fizikaverseny, Gyöngyös
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2014. október 10-én LEJÁRT. |
P. 4649. Távcsövünkkel a teleholdat nézzük. Eközben valaki tréfából eltakarja a távcső objektívjének a felét. Milyen változást látunk a távcső adta képen?
Csillagász szakkörök országos versenye, Dunaújváros
(3 pont)
P. 4650. Egy 25 literes gázpalackban 12 gramm hélium és 16 gramm oxigén keveréke található. Mekkora ennek a gáznak a sűrűsége és nyomása \(\displaystyle 27~^\circ\)C hőmérsékleten?
Tarján Imre emlékverseny, Szolnok
(3 pont)
P. 4651. Egy \(\displaystyle 24^\circ\) nyílásszögű éket beverünk egy fatuskóba. Legalább mekkora a tapadási súrlódási együttható a fatuskó és az ék között, ha az ék beszorul a fába?
Vermes Miklós emlékverseny, Sopron
(4 pont)
P. 4652. Nyolc darab, egyenként \(\displaystyle 100~\Omega\)-os fogyasztóból álló hálózatban az \(\displaystyle A\) és \(\displaystyle B\) pont között 50 V feszültséget mérünk.
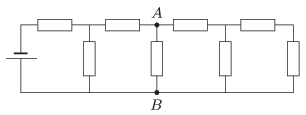
Mekkora teljesítményt vesz fel ez a fogyasztókör a telepből?
Mátrai Tibor fizikaverseny, Eger
(4 pont)
P. 4653. Egy tökéletesen sima felületű, rögzített gömb legmagasabban levő pontján egy kisméretű (tömegpontnak tekinthető) test van. Ha ezt a testet az egyensúlyi helyzetéből egy kicsit kitérítjük, akkor az egy ideig súrlódás nélkül csúszik a gömb felületén, majd onnan leválva leesik.
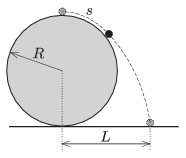
\(\displaystyle a)\) Mekkora \(\displaystyle s\) utat tesz meg a test a gömbön csúszva az elválás pillanatáig?
\(\displaystyle b)\) A gömb függőleges átmérőjétől számítva mekkora \(\displaystyle L\) távolságban esik a test a vízszintes alapra?
A gömb sugara \(\displaystyle R=1{,}5\) m.
Cornides István matematika-fizika verseny, Révkomárom (Szlovákia)
(4 pont)
P. 4654. Legalább mekkora vízszintes irányú erővel lehet felborítani egy jégen csúszó jégkockát? (A súrlódás elhanyagolható.)
Sopron-Pozsony fizikaverseny, Pozsony (Szlovákia)
(4 pont)
P. 4655. Középen tengelyezett, \(\displaystyle r=0{,}1~\)m sugarú, igen könnyű korong peremére fonalat tekertünk, annak szabad végére egy \(\displaystyle m=100~\)g tömegű testet erősítettünk. A koronghoz elhanyagolható tömegű rúd csatlakozik, amelynek végére, a korong tengelyétől \(\displaystyle R=0{,}2~\)m távolságban egy kisméretű, \(\displaystyle M\) tömegű testet rögzítettünk.
Kezdetben a rendszer az ábrán látható helyzetben nyugalomban van. A \(\displaystyle m\) tömeg alátámasztását hirtelen elvéve a \(\displaystyle M\) tömegű test az ábrán szaggatott vonallal jelölt \(\displaystyle 60^\circ\)-os helyzetet éppen eléri. Kis csillapítású lengések után a rúd egyensúlyba kerül, ekkor \(\displaystyle \varphi\) szöget zár be a függőlegessel.
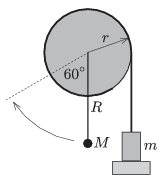
\(\displaystyle a)\) Mekkora a rúdon levő test \(\displaystyle M\) tömege?
\(\displaystyle b)\) Mekkora a \(\displaystyle \varphi\) szög?
\(\displaystyle c)\) Az egyensúlyi helyzetből kicsit kimozdítva a rendszert, mekkora rezgésidejű mozgás jön létre?
Izsák Imre Gyula természettudományi fizikaverseny, Zalaegerszeg
(5 pont)
P. 4656. Ugyanabban a pontban felfüggesztett három egyenlő hosszú fonálon három azonos nagyságú és tömegű kis gömb függ. Mindegyiknek ugyanakkora töltést adva mekkora sugarú körön fognak elhelyezkedni?
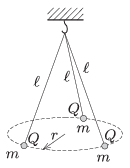
Adatok: \(\displaystyle \ell=20\) cm, \(\displaystyle m=1{,}3~\)gramm, \(\displaystyle Q=1{,}2\cdot10^{-7}\) C.
Francia érettségi feladat
(5 pont)
P. 4657. A mennyezethez rögzített 1 dm\(\displaystyle {}^2\) keresztmetszetű hőszigetelő hengerben levegő van. A levegő térfogata kezdetben 3 liter, hőmérséklete 300 K. A gázt elzáró, könnyen mozgó dugattyú szintén hőszigetelő, tömege 10 kg. A dugattyúhoz erősített zsinóron egy másik 10 kg-os test függ, a talaj felett 10 cm magasan. A levegőt lassan addig melegítjük, míg a térfogata 4,4 liter lesz.
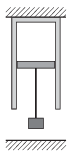
\(\displaystyle a)\) Mekkora a végállapotban a gáz hőmérséklete?
\(\displaystyle b)\) Mennyi hőt kellett közölni a gázzal?
Tornyai Sándor fizikaverseny, Hódmezővásárhely
(5 pont)
P. 4658. Hány neutron keletkezik egy nap alatt a Paksi Atomerőmű egy reaktorában, illetve a BME Oktatóreaktorában? (Feltesszük, hogy mindkét reaktor folyamatosan, 24 órán át üzemel.)
Adatok: egy paksi reaktor hőteljesítménye 1485 MW, az oktatóreaktor maximális hőteljesítménye 100 kW. Egy hasadás során 185 MeV energia szabadul fel, és átlagosan 2,43 neutron keletkezik.
Szilárd Leó nukleáris fizikaverseny, Paks
(3 pont)
P. 4659. 20 cm sugarú, vékony falú fémgömb belsejében koncentrikusan egy 10 cm sugarú fémgolyót helyezünk el. A belső golyót a külső gömbön levő nyíláson keresztül egy nagyon hosszú vezetékkel földeljük. A külső gömbnek \(\displaystyle 10^{-8}\) C töltést adunk. Mennyi lesz most a külső gömb potenciálja?
Nemzetközi fizikaverseny feladata
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

