 |
A P. 4655. feladat (2014. szeptember) |
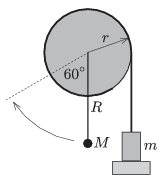
P. 4655. Középen tengelyezett, \(\displaystyle r=0{,}1~\)m sugarú, igen könnyű korong peremére fonalat tekertünk, annak szabad végére egy \(\displaystyle m=100~\)g tömegű testet erősítettünk. A koronghoz elhanyagolható tömegű rúd csatlakozik, amelynek végére, a korong tengelyétől \(\displaystyle R=0{,}2~\)m távolságban egy kisméretű, \(\displaystyle M\) tömegű testet rögzítettünk.
Kezdetben a rendszer az ábrán látható helyzetben nyugalomban van. A \(\displaystyle m\) tömeg alátámasztását hirtelen elvéve a \(\displaystyle M\) tömegű test az ábrán szaggatott vonallal jelölt \(\displaystyle 60^\circ\)-os helyzetet éppen eléri. Kis csillapítású lengések után a rúd egyensúlyba kerül, ekkor \(\displaystyle \varphi\) szöget zár be a függőlegessel.
\(\displaystyle a)\) Mekkora a rúdon levő test \(\displaystyle M\) tömege?
\(\displaystyle b)\) Mekkora a \(\displaystyle \varphi\) szög?
\(\displaystyle c)\) Az egyensúlyi helyzetből kicsit kimozdítva a rendszert, mekkora rezgésidejű mozgás jön létre?
Izsák Imre Gyula természettudományi fizikaverseny, Zalaegerszeg
(5 pont)
A beküldési határidő 2014. október 10-én LEJÁRT.
Megoldás: \(\displaystyle a)\) \(\displaystyle M=105\) g.
\(\displaystyle b)\) \(\displaystyle \sin\varphi=\frac{3}{2\pi};~~\varphi=28{,}5^\circ.\)
\(\displaystyle c)\) \(\displaystyle T=1{,}06~\)s.
Statisztika:
58 dolgozat érkezett. 5 pontot kapott: Asztalos Bogdán, Balogh Menyhért, Berta Dénes, Blum Balázs, Forrai Botond, Kasza Bence, Kovács Péter Tamás, Molnár 128 Szilárd, Olosz Balázs, Öreg Botond, Sáfrán Péter, Sal Kristóf, Südi István, Tompa Tamás Lajos. 4 pontot kapott: 38 versenyző. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2014. szeptemberi fizika feladatai
