Variációk a SET témájára

A játék

Marsha Jean Falco genetikus 1974-ben Cambridge-ben dolgozott: az epilepsziás megbetegedés öröklődését kutatta a német juhászkutyák között. Hogy az állatok génkombinációit könnyebben össze tudja hasonlítani, kártyákra írta az adatokat. Észrevette, hogy bizonyos információblokkok sok állat esetén megegyeznek, ezért az egyszerűség kedvéért egy-egy blokk leírása helyett ábrákat rajzolt a kártyákra. Ezután összefüggést keresett a kártyák és az öröklődés között, azaz bizonyos mintákat keresett a kártyák között. A lapokat kiteregette egy asztalra, majd munkatársaival elkezdtek azonos, vagy éppen különböző mintájú kártyákat keresni.

Ekkor jött az ötlet, hogy ebből akár egy játékot is lehetne készíteni. A családjával és a barátaival kidolgozták a SET kártyajátékot. 17 évvel később, 1991-ben családja unszolására az akkorra teljesen kidolgozott, kipróbált, megszeretett játékot bevezette a játékpiacra.

A játék azóta óriási siker lett, nagyrészt annak köszönhetően, hogy a szabályok könnyen érthetők, minden korosztály élvezi, és szinte akárhányan játszhatják egyszerre. Érdekes, hogy bár kifejezetten matematikai jellegű játékról van szó, mégis tizenegy-két éves gyerekek sokszor sokkal ügyesebben játsszák, mint esetleg matematikus szüleik. Ennek oka, hogy nem annyira a logikánkra vagy tudásunkra van szükség a nyeréshez, inkább a mintákat felismerő képességünkre.

A játékot két vagy több játékossal, speciális kártyákkal játszhatjuk: minden kártyán 1, 2 vagy 3 rombusz, hullám vagy ovális forma látható, piros, zöld vagy lila színben, csíkos, üres vagy teli kitöltéssel. (Minden lehetséges kombinációból pontosan egy.) A játék kezdetekor 12 kártyát helyezünk az asztalra színnel felfelé, majd mindenki elkezdi vizsgálni őket, SET-et keresve. SET-et három olyan kártya alkot, melyek esetében mind a négy tulajdonságra teljesül, hogy vagy mindhárom kártya ugyanolyan, vagy mindhárom különböző.

Például SET-et alkotnak a következők:

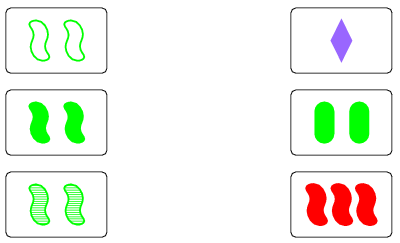
Ha valaki talált egy SET-et, akkor azt elveszi, és a kártyák helyére újabb kártyák kerülnek. Ha a játékosok megegyeznek abban, hogy az asztalon lévő kártyák között nincs SET, akkor újabb három kártya kerül az asztalra.

A játéknak akkor van vége, ha elfogynak a lapok, vagy ha már csak az asztalon vannak kártyák, és ezek között nincs SET. Az a játékos nyer, aki a legtöbb SET-et találta meg.

A következő részben néhány egyszerű kombinatorikai kérdést vizsgálunk meg a játékkal kapcsolatban.

Kombinatorikus megközelítés

1. Hány kártya van egy csomagban? Összesen 4 tulajdonság van (darab, kitöltés, szín, forma), mindegyik 3-3-féle lehet, így összesen 3⁴=81 darab kártya van egy pakliban.

2. Hány SET van összesen? Első lépésként gondoljuk meg, hogy ha adott két kártya, akkor azokhoz egyértelműen létezik egy harmadik, mellyel együtt SET-et alkotnak, mivel mind a négy tulajdonság esetében megnézzük, hogy a két adott kártya ugyanolyan-e, és ha igen, akkor a harmadiknak is ilyennek kell lennie, míg ha nem, akkor a harmadik kártyának mindkettőtől el kell térnie. Mivel minden lehetséges darab-kitöltés-szín-forma kombinációból pontosan egy van, azért ily módon egyértelműen meghatároztuk a hiányzó kártyát. Tehát bármely két kártya pontosan egy SET-ben van benne.

Ezek szerint először meg kell számolnunk, hányféleképpen választhatunk ki a 81 lap közül 2-t, ez nyilván

\(\displaystyle \binom{81}{2}=3240. \)

Ekkor azonban minden (a;b;c) SET-et háromszor számoltuk, mivel megszámoltuk egyszer, amikor a-t és b-t, egyszer, amikor a-t és c-t, és egyszer, amikor b-t és c-t választottuk ki. Ezért a fenti eredményt még el kell osztanunk 3-mal:

\(\displaystyle \frac{\binom{81}{2}}{3}=1080 \)

SET-et találhatunk a 81 lap között.

3. Egy kártya hány SET-ben van benne? Ha az adott kártya mellé választunk még egyet, akkor a SET harmadik lapja már egyértelmű. Egy adott kártya mellé 80-féle másik lapot választhatunk. Ekkor viszont minden (a;b;c) SET-et kétszer számoltunk: egyszer, amikor az adott a mellé b-t, és egyszer, amikor c-t választottuk. Tehát minden kártya \(\displaystyle \frac{80}{2}=40\) SET-ben van benne.

4. Egy játék alatt maximum hány SET-et találhatnak meg összesen a játékosok? A kérdést nyilván így is feltehetjük: előfordulhat-e, hogy minden kártya odakerül valamelyik játékoshoz, tehát összesen \(\displaystyle \frac{81}{3}=27\) SET-et találnak? Megint másként: beoszthatjuk-e az összes kártyát hármas csoportokba úgy, hogy minden csoportban egy SET legyen? (,,SET-ekbe rendezhetjük-e'' a kártyákat?)

A válasz nyilván igen. Például egy csoportba kerüljenek azok a lapok, melyeken ugyanannyi, ugyanolyan kitöltésű és színű minta van. (Például azok a kártyák, melyeken egy piros csíkos forma van: egy piros csíkos rombusz, egy piros csíkos hullám és egy piros csíkos ovális.) Könnyen meggondolhatjuk, hogy ekkor minden kártyát elhelyeztünk egy csoportba és minden kártyát csakis egy csoportba helyeztünk el, és nyilván minden csoport SET-et alkot.

5. Lehetséges-e, hogy a maximálisnál csak ,,kicsit'' kevesebb, azaz csak 26 SET-et találnak összesen a játékosok? Másképp feltéve a kérdést: lehetséges-e, hogy a játék végén három lap marad az asztalon?

A válasz: nem. Ezt a következő módon bizonyíthatjuk:

Állítás. Ha 78 kártyát SET-ekbe rendeztünk, akkor biztos, hogy a maradék három kártya is SET-et alkot.

Bizonyítás. Indirekt úton bizonyítunk.

Tegyük fel, hogy a maradék három kártya nem alkot SET-et. Ez azt jelenti, hogy találunk egy olyan tulajdonságot, melyből két egyforma és egy különböző kártya van az asztalon (ugyanis ha nem lenne ilyen tulajdonság, az azt jelentené, hogy minden tulajdonságra igaz, hogy három különböző vagy három egyforma lap van az asztalon, ez pedig azt jelentené, hogy a három kártya SET-et alkot). Az általánosság megsértése nélkül tegyük fel, hogy két lila és egy piros kártya maradt az asztalon.

Ez azt jelenti, hogy a többi piros és lila kártyát, tehát 26 piros és 25 lila kártyát sikerült SET-ekbe rendeznünk. Ezek között lehet olyan SET, melyben minden kártya piros, ezek számát jelöljük p-vel; lehet olyan, melyben minden kártya lila, ezek számát jelölje l; végül lehet olyan, melyben minden kártya más színű, ezek számát jelölje x.

Számoljuk meg a SET-ekben a piros kártyákat: p darab piros SET van, ez 3p darab kártya, és minden vegyes színű SET-ben még egy piros lap van, ez még x darab kártya. Tehát:

3p+x=26.

Hasonlóan a lila színű kártyákra:

3l+x=25.

A két egyenletből:

3(p-l)=1,

ami nyilván ellentmondás, mivel p és l egész számok.  \(\displaystyle \square\)

Változatok

Ugyanezekkel a kártyákkal sok egyéb játékot is játszhatunk, kis gondolkodással saját szabályokat, saját játékokat is kitalálhatunk. Például a következőt, melyet két játékos játszhat:

Helyezzük az asztalra az összes kártyát színével fölfele. Az első játékos (legyen A) választ magának egy kártyát, úgy, hogy ellenfele (B) is lássa. Ezután B következik, és így tovább, felváltva választanak kártyát a játékosok.

Az a játékos nyer, akinek a kezében előbb lesz SET. Ekkor tehát a cél, hogy úgy szerezzünk SET-et, hogy közben arra is figyelünk, nehogy az ellenfélnek hamarabb összegyűljön.

Hogy átláthatóbb és könnyebben elemezhető legyen a játék, egyszerűsítsük le: válasszunk egy formát és egy telítettséget, például az üres oválist, és csak az üres oválist ábrázoló kártyákkal játsszunk! Ekkor csak a szín és a szám változik, így összesen 3^.3=9 kártya marad. Az egyszerűség kedvéért azt is mondhatjuk, hogy van kilenc kártyánk, mindegyiken egy 1 és 3 közti szám szerepel piros, lila vagy zöld színnel írva. SET-et alkot három kártya, ha a színre és a számra is teljesül, hogy mindhárom kártya különböző, vagy mindhárom azonos. A cél továbbra is az, hogy az ellenféllel felváltva választva lapot hamarabb gyűjtsünk össze SET-et, mint a másik játékos.

Adja magát az ötlet, hogy a kilenc kártyát rendezzük négyzet alakba: például az első oszlopban a piros, a másodikban a lila, a harmadikban a zöld lapok, míg az első sorban az 1-et, a másodikban a 2-t, a harmadikban a 3-at ábrázoló kártyák szerepeljenek.

Ekkor láthatjuk, hogy minden sor, minden oszlop és mindkét átló SET-et alkot. Azt gondolhatnánk, hogy ezek szerint ez a játék éppen olyan, mint a háromszor hármas pályán játszott amőba (Tic Tac Toe): a játékosok felváltva elhelyezik a jelüket (x vagy o) a táblázat egy mezőjébe (azaz jelen esetben választanak egy lapot), és az nyer, akinek hamarabb lesz három jele egy sorban, vízszintesen, függőlegesen, vagy átlósan (azaz akinek hamarabb lesz SET a kezében). Az egyezés mégsem teljes, mivel a mi esetünkben további SET-eket találhatunk: a1, b3, c2 mezők (azaz a piros 1, lila 3, zöld 2 lapok) is SET-et alkotnak, és hasonlóan ennek mindhárom 90^o-os elforgatottja is SET-et alkot.

Azt látjuk tehát, hogy minden kártya, azaz minden mező pontosan négy SET-ben van benne: a függőleges, a vízszintes, és a két átlós irány által meghatározott SET-ekben. (Valóban: könnyen látható, hogy minden kártya négy SET-ben van benne: adott a kártya mellé kiválaszthatom bármelyiket (b) a többi nyolc közül, akkor már egyértelmű lesz a SET harmadik lapja (c), ugyanakkor így minden (a;b;c) SET-et kétszer számoltunk: egyszer, amikor a mellé b-t, és egyszer, amikor c-t választottuk, tehát minden lap \(\displaystyle \frac{8}{2}=4\) SET-ben van benne. Így tehát biztos, hogy a táblázatban megtaláltunk minden SET-et.)

Készíthetünk azonban olyan pályát, ahol mégis a megszokott amőba játékunkat játszhatjuk: rajzoljuk meg a háromszor hármas táblázatot egy gumilapra, az első és a harmadik sort összeillesztve hajlítsunk belőle hengert, majd az első és a harmadik oszlopot összeillesztve készítsünk tóruszt!

Ha ezen a pályán kezdünk el a szokásos szabályokkal amőbát játszani, pontosan akkor fog az egyik játékos nyerni, amikor az általunk alkotott játékban.

Minden gyerek, aki játszott háromszor hármas pályán amőbát, hamar rájött, hogy ha két jól játszó játékos kerül egymással szembe, mindig döntetlen lesz a végeredmény. Vajon igaz ez a tóruszon játszott amőbára is?

A válasz: nem. Itt mindenképp úgy lesz vége a játéknak, hogy valamelyik játékos nyer.

Állítás. A tóruszon játszott Tic Tac Toe-nak mindig van győztese.

Bizonyítás. Mivel 9 mezőre helyezték el felváltva a játékosok a jelüket, a játék végén az egyik jelből 5, a másikból 4 darab lesz. Tegyük fel, hogy 5 darab x van a táblán. Állításunk ekkor az, hogy biztosan található ezek között három olyan, amely egy vonalba esik.

Tegyük fel indirekt, hogy az öt x között nincs három, ami egy vonalba esik. Ez csak úgy lehet, hogy például két vízszintes sorba 2-2, a harmadikba 1 darab x került. Tekintsük ezt az egyet! Tudjuk, hogy minden mező, így ez is négy ,,nyerő hármas''-ban van benne, ezek közül az egyik az a sor, ahol elhelyezkedik. Feltevésünk szerint itt nincs másik x, ez azt jelenti, hogy a többi négy x csak a többi három ,,nyerő hármas'' mezői között lehet. Ekkor viszont biztosan van olyan ,,nyerő hármas'', amelybe az adott x-en kívül még kettő került, mert ha ilyen nem lenne, az azt jelentené, hogy összesen legfeljebb négy x van a táblán, márpedig abból indultunk ki, hogy öt van. Ez viszont azt jelenti, hogy ebben a vonalban mindhárom mezőben x szerepel, tehát mégiscsak találtunk három, egy vonalba eső x-et. (A bizonyítás ötlete megtalálható Jürgen Bierbrauer és Yves Edel: Bounds on affine caps c. cikkében, http://en.scientificcommons.org/339409.)  \(\displaystyle \square\)

A játék kártyáinak felhasználásával további játékra és gondolkodásra, elemzésre érdemes új játékszabályokat alkothatunk. Néhány ötletet találhatunk, vagy akár on-line játszhatunk a www.setgame.com oldalon.

Deme-Farkas Rita
ELTE TTK V. éves
matematika tanárszakos hallgató