Kiss Elemér
Kétszáz éve született Bolyai János
Ebben az évben, december 15-én emlékezünk meg Bolyai János születésének kétszázadik évfordulójáról. Ő volt az első olyan magyar matematikus, aki - Eötvös Loránd szavaival - világraszólót alkotott. Nagy tudósunkról sajnos nem maradt fenn hiteles kép. Így az utókor nem ismerhette meg arcvonásait, csak 48 éves korában készült útlevele alapján tudjuk, hogy középtermetű, kékszemű, hosszúkás arcú férfi volt. Bár arcélét nem ismerjük, életét és munkásságát szerencsére számos mű méltatta. Rangos monográfiák, sok tudományos dolgozat és népszerűsítő cikk ismerteti életútját, a geometriában elért korszakalkotó felfedezését s a modern matematika kialakításában játszott szerepét.
Bolyai Jánosnak élete folyamán csak egyetlen műve jelent meg nyomtatásban, A tér abszolút igaz tudománya, röviden az Appendix. Ezzel a munkájával hozta létre az ún. nemeuklidészi geometriát. Megtörte az euklidészi geometria egyeduralmát, felszabadította az utat az emberi gondolkodás előtt a tér másként való felfogása számára, utat nyitott a huszadik század fizikai elméletei előtt, melyek világképünket gyökeresen megváltoztatták. De Bolyai nem csak a geometriában alkotott nagyot. Ő egyetemes matematikai zseni volt, aki kora matematikájának minden olyan ágával foglalkozott, amelyekről tudomást szerzett. Napjait átszőtte a szegénység, a betegség és a fájó megnemértés. Geometriai műveinek jelentőségét a halála utáni évtizedekben ismerték el, míg más matematikai felfedezéseiről még későbben, csak a közelmúltban értesülhettünk.
Bolyai János életútja
Bolyai János 1802. december 15-én született Kolozsvárott. Apja a marosvásárhelyi Református Kollégium későbbi legendás tanára Bolyai Farkas (1775-1856), anyja Árkosi Benkő Zsuzsanna (1780-1821) egy kolozsvári sebész leánya. Gyermekkorát Marosvásárhelyen és Domáldon töltötte. Erről az időszakról a fiára büszke apa ifjúkori barátjához, Carl Friedrich Gausshoz (1777-1855) írt leveleiben részletesen beszámolt. Elmondja, hogy az ötéves kisfiú játékból az égbolt sok csillagának nevét megtanulta, ismeri az egyszerűbb geometriai alakzatokat, tisztában van a szinusz fogalmával. Az írás-olvasást hatéves korában szinte magától sajátította el, rá egy évre már németül és hegedülni is tanult. János rendszeres oktatását kilencéves korában kezdik meg. Először a szülői háznál, az apja által kiválasztott legjobb diákok foglalkoznak vele. Matematikára apja tanította. Tizenkét esztendős korától volt a marosvásárhelyi kollégium rendes tanulója, ahol 1817-ben leteszi a mai érettséginek megfelelő vizsgát.
A matematikához fűződő érdekes gyerekkori gondolatairól maga János is nyilatkozik. Fennmaradt kéziratos hagyatékában olvashatjuk a következő mondatokat: ,,Már kisgyermek koromban feltettem magamnak a kérdést, hogy végtelen sok prímszám létezik-e?'' és ,,gyermekkoromban magamtól találtam, hogy
\(\displaystyle \lim_{m\to\infty}\left(1+\frac{k}{m}\right)^{\!\!m}=e^k.mbox{\emph{''}}\)
Bolyai Farkas azt szerette volna, ha rendkívül tehetséges fia Göttingenben annál a Gaussnál folytatná tanulmányait, akivel egyetemi éveik alatt életre szóló barátságot kötött. Ezt megírta az akkor már nagyhírű matematikusnak, de levelére nem kapott választ. Ezért hosszas töprengés után úgy határozott, hogy fiát a bécsi hadmérnöki akadémiára küldi továbbtanulni. János Bécsben 1818 augusztusában német nyelven sikerrel letette a felvételi vizsgát, és ezzel megkezdődött katonai pályafutása.
Bolyai János mindig jó tanuló volt és hadmérnöki akadémiai évei alatt is rendszeresen foglalkozott matematikával. Jegyzeteiben már ekkor felvillannak eredeti ötleteinek szikrái. 17 évesen szép megoldást talál egy adott szög három egyenlő részre való felosztására körző és vonalzó, valamint az egyenlő oldalú hiperbola egyik ágának felhasználásával. 1820 körül kezdett intenzíven foglalkozni a párhuzamosok posztulátumával annak ellenére, hogy apja megpróbálja lebeszélni erről: ,,Az Istenért kérlek! Haggy békét a paralleláknak, ...'' - írja fiának Farkas.
Tanulmányait 1823-ban fejezte be. Ezután kinevezték alhadnagynak és a temesvári erődítési igazgatósághoz osztották be. A ,,parallelákról'' Bécsben elkezdett töprengései itt értek be. Temesváron fedezi fel ,,éppen télben, éjfél tájban'' a nem egészen 21 éves Bolyai János az abszolút geometria alapképletét. Erről apjának 1823. november 3-án számolt be nevezetes ,,temesvári levelében''. Bolyai János az 1823-1825-ös években fogalmazta meg és foglalta egységes rendszerbe az abszolút geometria alapjait. A már kidolgozott elméletét 1825 elején megmutatta apjának, s 1826-ban egy német nyelvű változatát átadta Wolter von Eckwehr (1791-1857) századosnak, közvetlen parancsnokának és volt bécsi matematikatanárának. Sajnos ennek a kéziratnak nyoma veszett. Katonai pályafutása alatt Bolyai Temesvár után még Aradon, Lembergben, végül pedig Olmützben szolgált. Ezekben az években többször betegeskedett. 1833-ban saját kérésére másodosztályú kapitányi rangban nyugdíjazták.
Közben 1831-ben különlenyomatban megjelenik Bolyai János nagy műve a Tér abszolút igaz tudománya, amelyet Bolyai Farkas szinte azonnal, 1831. június 20-án elküldött Gaussnak, akinek véleményét kérte fia munkájáról. Ez a példány elveszett, ezért 1832. január 16-án János művét újból megküldi barátjának. Gauss 1832. március 6-án kelt válasza - ,,... ha fiad munkáját megdicsérném, akkor magamat dicsérném, mivel a mű egész tartalma, az út, amelyet fiad követ és az eredmények, amelyekre jutott, majdnem végig megegyeznek részben már 30-35 év óta folytatott elmélkedéseimmel'' - Bolyai Jánost lesújtotta, elkeserítette. Becsapott embernek érezte magát. Különös, hogy Gauss Ch. L. Gerling (1788-1864) marburgi matematikusnak három héttel korábban írt levelében Bolyait ,,elsőrangú lángésznek'' tartja. Kár, hogy ezeket a szavakat nem Bolyai Farkasnak írta.
Bolyai János nyugalomba vonulása után 1833-ban visszatért Marosvásárhelyre. Egy éven át apjánál lakott, majd 1834-ben elköltözött egy távoli faluba, Domáldra. Domáldon írja meg a Responsio című munkáját a komplex számokról, amelyet egy lipcsei tudományos társaság pályázatára küld el 1837-ben. Ez a próbálkozás újabb kudarcot jelentett Jánosnak. A bírálók nem értették meg a dolgozatában foglaltakat, ezért azt elutasították. Bolyai 1846-ban újból Marosvásárhelyre költözött és itt élt az 1860. január 27-én bekövetkezett haláláig. 1848-ban nagy meglepetés érte. Ekkor jutott Nyikolaj Ivanovics Lobacsevszkij (1793-1856) 1840-ben Berlinben megjelent könyvéhez, melynek tartalma sok részletében megegyezik az Appendixével. Nem nehéz elképzelni milyen izgalommal olvasta végig ezt a munkát, ám miután alaposan áttanulmányozta a legnagyobb elismeréssel nyilatkozott róla.
Bolyai János egész életében dolgozott. Az Appendix és Responsio megalkotása után is töretlen erővel folytatta kutatásait. Mindig a matematikának élt. Ebben sem a katonai szolgálat, sem későbbi betegségei nem tudták megakadályozni. Az 1820-as évek az Appendix kidolgozásának jegyében teltek el, de ugyanakkor már algebrai, számelméleti kérdések és a komplex számok elmélete is lekötötte a figyelmét. Élete második felében, nyugdíjaztatása után sem pihent. Napestig ült íróasztala mellett, hogy fóliáns nagyságú papírjait vagy sokszor apró papírszeletkéit teleírja. Ennek eredménye az a hatalmas kéziratos hagyaték, amelyet halálakor ránkhagyott. Kéziratainak nagy részét - mintegy 14 000 oldalt - ma a marosvásárhelyi Teleki-Bolyai Könyvtárban őrzik, de értékes Bolyai-gyűjteménye van az MTA Könyvtárának is Budapesten. E feljegyzésekben rejtőztek azok a ,,kincsek'' (Bolyai nevezte így az általa felfedezett matematikai tételeket), amelyeket csak az utóbbi évek kutatásai hoztak felszínre.
A tér abszolút igaz tudománya
Az Appendix Bolyai János főműve. A latin nyelven rendkívüli precizitással és tömörséggel megírt mű a matematikai irodalom legtökéletesebb munkái közé tartozik, amelyet napjainkig minden jelentősebb nyelvre lefordítottak. Már első idegen (francia) nyelvű fordítója Guillaume-Jules Hoüel (1823-1886) bordeaux-i egyetemi tanár így nyilatkozott: ,,Ez az Appendix egy kimagaslóan értékes munka''. Később Georg Bruce Halsted (1853-1922) texasi (USA) professzor, aki angolra ültette át az Appendixet megállapítja: ,,ez a huszonnégy oldal a legrendkívülibb két tucat oldal a gondolkodás történetében''.
Bolyai János ezzel a munkájával valóban világraszólót alkotott. Megoldotta a geometria leghosszabb ideig, több mint 2000 évig ellenálló, ún. párhuzamosok problémáját.
Mi volt ez a probléma?
A mértan tudományának első egzakt munkája Euklidész Elemek (Kr. e. III. évszázad) című könyve volt. A mű legnagyobb érdeme, hogy a geometriai ismereteket egységes logikai rendszerbe foglalta, melyben kevés számú állításból, logikusan, egymásra épülve következnek az újabb és újabb állítások, deduktív bizonyítás útján. Euklidész öt olyan alaptételre (axiómára, posztulátumra) építette fel geometriáját, amelyeket bizonyítás nélkül elfogadott. Ezek közül az első négy (az egyenes bármeddig meghosszabbítható, minden derékszög egyenlő, ...) igen ,,egyszerű'', ,,szemléletes'', könnyen elfogadható. Az V. posztulátum (egyes kiadásokban XI. axióma) - ha egy egyenes másik két egyenest úgy metsz, hogy a metsző egyenes ugyanazon oldalán keletkezett két szög összege kisebb, mint két derékszög, akkor ezek az egyenesek a végtelenbe meghosszabbítva metszik egymást - már nem tűnik annyira ,,nyilvánvalónak'' mint a többi. Ezt a posztulátumot a matematikusok már a kezdetekben is kritikával fogadták. Könyvében maga Euklidész is csak a 29. tétel bizonyításánál használja fel először. Sokan úgy próbáltak megszabadulni tőle, hogy megkísérelték azt könnyebben beláthatóval, azaz vele ekvivalenssel helyettesíteni (egy kijelentésről akkor mondjuk, hogy ekvivalens az V. vagyis az euklidészi párhuzamossági posztulátummal, ha e kijelentés, a többi axióma - az ún. maradék axiómarendszer - és az ezekből levezetett tételek segítségével bizonyítani tudjuk az V. posztulátumot és fordítva, a kijelentés is csak az V. posztulátum segítségével bizonyítható).
Miután ezek a próbálkozások nem hoztak lényeges haladást, a matematikusok hosszú időn át megkísérelték az V. posztulátumot bebizonyítani. Valamennyi kísérlet hiábavalónak bizonyult. Döntő fordulat akkor állott elő, amikor a maradékrendszerhez az V. posztulátum tagadását csatolták és így próbálták felépíteni a geometriát. Furcsa, a szemlélet számára szokatlan tételek adódtak, de ezek egymással szemben nem mutattak fel ellentmondást.
Bolyai János volt az, aki időben legelőször olyan általános geometriát épített föl, amely az V. posztulátumot sem nem állítja, sem nem tagadja, hanem mellőzi. Úgy értelmezte a párhuzamosságot, hogy az egybefoglalja az V. posztulátum állításának és tagadásának a lehetőségét. Eszerint ennek az általános, Bolyai által abszolútnak nevezett geometriának sajátos esete mind az euklidészi (a \(\displaystyle \Sigma\)-rendszer), mind a nemeuklidészi vagy más néven hiperbolikus (az S-rendszer) geometria. Bolyai nagy érdeme abban állt, hogy fölépítette az abszolút geometriát és azon belül a hiperbolikus geometriát.
Bolyai János megtartja Euklidész posztulátumait, kivéve az V.-et. Mindazokat az alapfeltevéseket, melyek pontoknak egyenesek és síkok által való összekötésére, távolságoknak és szögeknek változatlan nagyságban való átvitelére, a háromszögek egybevágóságára stb. vonatkoznak, az S-rendszer éppen úgy megköveteli, mint a közfelfogás. Az eltérés a párhuzamosság értelmezésével kezdődik, amelynek fogalmát Bolyai az Appendix 1.S-ban vezeti be. Említsük meg ezt az értelmezést:
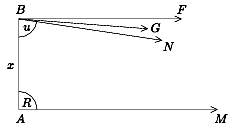
1. ábra
A \(\displaystyle \overrightarrow{BN}\) irányított félegyenesről
akkor mondja, hogy párhuzamos az \(\displaystyle \overrightarrow{AM}\) irányított félegyenessel,
ha \(\displaystyle \overrightarrow{BN}\) a félsugaraknak a BA helyzetéből
kiindulva B körüli az óramutató járásával ellenkező irányú
forgása közben előálló olyan félegyenes, amely már éppen nem metszi
AM-et (1. ábra), elpattan tőle. Bolyai János szerint
világos, hogy bármely az AM egyenesen kívül fekvő B
pontból (az AM és B síkjában) kiindul ilyen 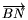 , de csak egy, és hogy
, de csak egy, és hogy
| (1) | BAM +ABN\(\displaystyle \angle\) +ABN\(\displaystyle \angle\) 2R 2R |
(R a derékszöget jelenti).
Az így értelmezett párhuzamosságot abszolút
párhuzamosságnak nevezzük, ha pedig (1)-ben csak a < jelet engedjük
meg, akkor hiperbolikus párhuzamosságról
beszélünk. A hiperbolikus esetben az AM egyeneshez a
B ponton át két - ellentétesen irányított -
párhuzamos egyenes tartozik. Ekkor vannak még olyan 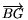 félegyenesek is, amelyek sem nem
párhuzamosak
félegyenesek is, amelyek sem nem
párhuzamosak 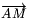 -mel, sem nem metszik azt.
-mel, sem nem metszik azt.
Megjegyezzük, hogy Bolyai egyenesei nem feltétlenül ,,egyenesek'' a köznapi értelemben. Ezek félkörök, vagy más geometriai objektumok is lehetnek. A szemléltető ábrákon mégis köznapi értelemben használatos egyeneseket rajzolunk.
Bolyai János ebből az értelmezésből kiindulva felépítette a sík és a tér abszolút, az V. posztulátumtól független geometriáját. Íme két szép tétele:
1. <<\textsl>>Az abszolút síkgeometria Temesváron felfedezett alapösszefüggése (Appendix 29.S)

<<\textsl>>az u párhuzamossági szög és az x párhuzamossági távolság között létesít kapcsolatot (1. ábra). Itt e az Euler-féle szám (e=2,718 ...), k pedig egy, a teret jellemző pozitív valós szám.
E képlet szerint, ha 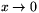 , akkor
, akkor
 . Hasonlóképpen, ha
. Hasonlóképpen, ha 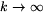 ,
akkor is
,
akkor is  . Az euklidészi geometriában a párhuzamossági
szög
. Az euklidészi geometriában a párhuzamossági
szög 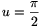 bármely x-re, ezért a fenti két eredmény
így értelmezhető: a hiperbolikus síkon ,,kicsiben'' (
bármely x-re, ezért a fenti két eredmény
így értelmezhető: a hiperbolikus síkon ,,kicsiben'' (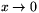 )
közelítőleg az euklidészi geometria érvényesül, és az
S-rendszer geometriája közeledik a
)
közelítőleg az euklidészi geometria érvényesül, és az
S-rendszer geometriája közeledik a  -rendszeréhez,
ha az S-rendszer állandója,
-rendszeréhez,
ha az S-rendszer állandója, 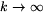 .
.
2. Bolyai János ,,abszolút szinusz-tétele'' (Appendix 25.S).
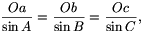
<<\textsl>>ahol Or az r sugarú kör
abszolút geometriai kerületét, A, B, C a
háromszög szögeit, a, b, c pedig a szemben lévő
oldalakat jelentik. Az abszolút trigonometria e tétele Bolyai János
egyik legszebb eredménye. Különösen egyszerű egybefoglalása egy  -beli és egy
S-beli tételnek. Az euklidészi geometriában Or=2
-beli és egy
S-beli tételnek. Az euklidészi geometriában Or=2 r. Ha ezt a
fenti összefüggésbe helyettesítjük és 2
r. Ha ezt a
fenti összefüggésbe helyettesítjük és 2 -vel egyszerűsítünk, megkapjuk a
szinusz-tétel ismert alakját. A hiperbolikus geometriában
-vel egyszerűsítünk, megkapjuk a
szinusz-tétel ismert alakját. A hiperbolikus geometriában 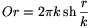 .footnoteItt
.footnoteItt 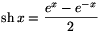 (a szerk. megj.). Ha most ezt
helyettesítjük a fenti képletbe és 2
(a szerk. megj.). Ha most ezt
helyettesítjük a fenti képletbe és 2 k-val egyszerűsítünk eljutunk a
hiperbolikus geometria szinusz-tételéhez:
k-val egyszerűsítünk eljutunk a
hiperbolikus geometria szinusz-tételéhez:
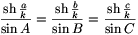
Bolyai János felfedezésével új fejezetet nyitott a tudomány történetében. Az abszolút geometria mélyrehatóan befolyásolta a későbbi kutatásokat. Egyik alapvető következménye annak a ténynek a felismerése volt, hogy az euklidészi geometria rendszere nem az egyetlen elképzelhető geometriai rendszer. Nagy szerepet játszott az Appendix az axiómatikus módszerek kidolgozásában. A nemeuklidészi geometriával szoros összefüggésben merült fel először az axiómarendszerek függetlenségének, ellentmondásmentességének, teljességének a kérdése.
Több mint két évezreden át tartott Euklidész geometriájának kizárólagos uralma. Aztán a XIX. század elején a tudományos élet színterén megjelent a nemeuklidészi geometria, amelyet három egymástól igen távol eső helyen, egymástól függetlenül és majdnem egyidőben fedezett fel Bolyai János, Gauss (aki bár több tulajdonságát felismerte az új geometriának, de semmit sem közölt) és Lobacsevszkij. Helyesen ítélt Bolyai Farkas, amikor fiát eredményeinek mielőbbi közzétételére bíztatta, mondván: ,,... az eszméknek mintegy megvan a maguk korszaka, amikor különböző helyeken egyidőben fedeztetnek föl, amint tavaszkor az ibolyák mindenütt kikelnek, ahol csak süt a nap''.
Az új geometria a kortársak részéről csak nehezen talált megértésre. Ahogyan ismertté kezdett válni, jelentek meg az ellene intézett támadások. A kétkedők meggyőzésében döntő szerepet játszottak a XIX. század második felében született, a hiperbolikus geometriát szemléltető modellek, amelyeket e geometria térképeinek nevezhetünk [6].footnote Ezeknek a modelleknek a léte bizonyítja azt, hogy amennyiben az euklidészi geometria ellentmondásmentes, akkor a hiperbolikus geometria is az. Ebből következik, hogy az V. posztulátum valóban nem vezethető le a geometria többi axiómájából (a szerk. megj.).
Bolyai János tisztában volt az Appendix jelentőségével. Tudta, hogy új világa majdan kihat egész szemléletünkre, befolyásolja az összes olyan tudományt, amelyekben a tér fogalma, szerkezete szerepet játszik. Így ír: ,,... a teljes napfogyatkozás pedig ... örökre eltűnt. És a szerzőben él az a meggyőződés, hogy e tárgy tisztázásával a tudomány igazi gyarapításának, az ész művelésének, és így az emberi sors lendítésének egyik legfontosabb és leglényegesebb lépése megtörtént''.
A komplex számok
Bolyai János másik nagy jelentőségű munkája a Responsio. Ebben a dolgozatban Bolyai korát megelőző gondolatokat vallott a komplex számok elméletében is. Tömör írásában főképpen a komplex számok precíz értelmezésével a geometriában játszott fontos szerepére mutat rá.
A Responsioban foglaltakkal azonban nem merültek ki Bolyai Jánosnak a komplex számokkal kapcsolatos vizsgálatai. Az utóbbi évtized kutatásai kiderítették, hogy Gauss-szal egyidőben, de tőle függetlenül felfedezte a komplex számok aritmetikáját is. Igaz, próbálkozásairól nem készített egy összefüggő dolgozatot, ám kéziratainak lapjairól összegyűjtve a tárggyal kapcsolatos följegyzéseit, megállapíthatjuk, hogy a komplex egészek oszthatóságának minden alapvető problémájával foglalkozott.
A ![\Bbb{Z}[i]:=\b\{a+bi\mid a,b\in\Bbb{Z},~
i=\sqrt{-1}\,\b\}](kepl817f8a6fdb47d4.gif) halmazt, vagyis az olyan a+bi alakú
komplex számok halmazát, ahol a és b egész számok, a
komplex egészek vagy Gauss-egészek halmazának nevezzük. Ebben a
halmazban is felépíthető a szokásos számelmélet megfelelője, vagyis
itt is beszélhetünk az oszthatóság, a maradékos osztás, a legnagyobb
közös osztó, a prímek és más fogalmakról éppen úgy, mint a racionális
egészek
halmazt, vagyis az olyan a+bi alakú
komplex számok halmazát, ahol a és b egész számok, a
komplex egészek vagy Gauss-egészek halmazának nevezzük. Ebben a
halmazban is felépíthető a szokásos számelmélet megfelelője, vagyis
itt is beszélhetünk az oszthatóság, a maradékos osztás, a legnagyobb
közös osztó, a prímek és más fogalmakról éppen úgy, mint a racionális
egészek 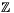 halmazában.
halmazában.
Ha adott  ,
,  komplex egészekhez található olyan
komplex egészekhez található olyan  komplex
egész, hogy
komplex
egész, hogy  =
=
 , akkor azt mondjuk, hogy
, akkor azt mondjuk, hogy  osztható
osztható  -val, vagy
-val, vagy  osztja
osztja  -t. Például
-t. Például  =1+8i
osztható
=1+8i
osztható  =2+i-vel, mert létezik a
=2+i-vel, mert létezik a  =2+3i
komplex egész úgy, hogy
1+8i=(2+i)(2+3i). Észrevesszük, hogy
=2+3i
komplex egész úgy, hogy
1+8i=(2+i)(2+3i). Észrevesszük, hogy  még osztható
a +1, -1, +i, -i, -2-3i, -2-i,
-3+2i, -1+2i, 3-2i, 1-2i és természetesen
a 2+3i komplex egészekkel is. Egy
még osztható
a +1, -1, +i, -i, -2-3i, -2-i,
-3+2i, -1+2i, 3-2i, 1-2i és természetesen
a 2+3i komplex egészekkel is. Egy  komplex egészet egységnek nevezünk, ha bármely komplex egésznek
osztója (
komplex egészet egységnek nevezünk, ha bármely komplex egésznek
osztója (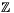 -ben +1 és -1 az egységek). Igazolható, hogy
-ben +1 és -1 az egységek). Igazolható, hogy ![\Bbb{Z}[i]](kepl62b2e4f0682c43.gif) egységei: +1, -1, +i, -i. Ha a
egységei: +1, -1, +i, -i. Ha a ![\beta\in\Bbb{Z}[i]](kepl51fbbddb0da74d.gif) egységszerese
egységszerese ![\alpha\in\Bbb{Z}[i]](kepl16dfe9b6885bf3.gif) -nek, akkor
-nek, akkor  -t az
-t az  asszociáltjának mondjuk. Az
asszociáltjának mondjuk. Az  komplex
egészet összetettnek nevezzük, ha két egységtől különböző komplex
egész szorzata, ezzel szemben ha a
komplex
egészet összetettnek nevezzük, ha két egységtől különböző komplex
egész szorzata, ezzel szemben ha a  (egységtől különböző) komplex egész ilyen
szorzótényezőkre való felbontással nem rendelkezik, akkor azt komplex
prímnek nevezzük. Az
(egységtől különböző) komplex egész ilyen
szorzótényezőkre való felbontással nem rendelkezik, akkor azt komplex
prímnek nevezzük. Az  =1+8i összetett komplex egész, a
=1+8i összetett komplex egész, a  =1+2i komplex
prím.
=1+2i komplex
prím.
Érdekes feladat annak eldöntése, hogy pontosan
melyek a ![\Bbb{Z}[i]](kepl62b2e4f0682c43.gif) halmaz prímelemei. Bolyainak sikerült megállapítania
(persze szigorú bizonyítások útján), hogy a komplex prímeket a
következő három osztály elemei (és ezek asszociáltjai) alkotják:
halmaz prímelemei. Bolyainak sikerült megállapítania
(persze szigorú bizonyítások útján), hogy a komplex prímeket a
következő három osztály elemei (és ezek asszociáltjai) alkotják:
a) 1+i,
b) a 4m+3 alakú racionális prímszámok,
c) a 4m+1 alakú racionális prímszámok komplex tényezői.
Vizsgáljuk meg részletesebben a fentieket! Kezdjük
mindjárt a c) ponttal. Mit jelent, hogy a 4m+1
alakú racionális prímszámok komplex tényezői? Pierre Fermat
(1601-1664) ún. karácsonyi tétele (alább még találkozunk vele) szerint
minden 4m+1 alakú prímszám előáll két négyzetszám
összegeként. Így például 5=4
.1+1=22+12 s ezért
=(2+i)(2-i)=(1+2i)(1-2i)=..., ugyanúgy
97=4 .24+1=92+42=
(9+4i)(9-4i)=
(4+9i)(4-9i)=.... A c) szerint tehát
2+i, 1-2i, 9+4i stb. komplex prímek. Az
a)-ban szereplő 1+i, 1-i, -1+i,
-1-i-vel együtt ezeket Bolyai János tökélyes prímeknek
nevezi. A b) pontban a 3, 7, 11, ... racionális
prímek találhatók. Ha ezeket komplex egészeknek tekintjük (3=3+0
.i, 7=7+0.i, ...)
akkor nem tudjuk két egységtől különböző komplex egész szorzatára
bontani, vagyis komplex prímek. Léteznek tehát olyan egész számok
amelyek úgy a 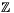 -ben, mint a
-ben, mint a ![\Bbb{Z}[i]](kepl62b2e4f0682c43.gif) -ben is prímek. Bolyai ezeket
abszolút prímeknek nevezte.
-ben is prímek. Bolyai ezeket
abszolút prímeknek nevezte.
Bolyai János a számelmélet több alapvető tételének
megfelelőjét is megoldja a komplex egészek halmazán. Így bebizonyítja,
hogy érvényes a komplex egészek egyértelmű prímfelbontása, foglalkozik
a kongruenciák elméletével ![\Bbb{Z}[i]](kepl62b2e4f0682c43.gif) -ben és más problémákkal is,
amelyekre itt most nem térünk ki. Még csak azt jegyezzük meg, hogy
elméletét sikeresen alkalmazta több számelméleti tétel
bizonyításánál.
-ben és más problémákkal is,
amelyekre itt most nem térünk ki. Még csak azt jegyezzük meg, hogy
elméletét sikeresen alkalmazta több számelméleti tétel
bizonyításánál.
Számelmélet
Az eddig megjelent valamennyi Bolyai-monográfia szerzőjének véleménye szerint az abszolút geometria megalkotója a számelmélet terén nem ért el semmilyen említésre méltó eredményt. Kéziratos hagyatékának lapjai ennek a véleménynek éppen az ellenkezőjéről tanúskodnak. Bolyai Jánost a számelmélet valósággal elbűvölte. Így ír erről: ,,A számelméletben az egész tan legfontosabb, legszebb, legérdekesebb, legkecsesebb feladatait találjuk''. Különösen a prímszámokkal kapcsolatos kérdések kötötték le a figyelmét. Véleménye szerint: ,,Az egész számtan mezején alig van szebb és érdekesebb, mint a prímszámok oly mély homályban rejlő titka''.
Egy olyan eljárást keresett, amelynek segítségével bármely racionális prímszám megfelelő képlettel kifejezhető (amint láttuk a komplex prímeket megtalálta). Egy időben a prímszámképletet a kis Fermat-tételben vélte felfedezni. Ez a tétel azt mondja ki, hogy ha p egy prímszám, a egy olyan egész szám, amely nem osztható p-vel, akkor az ap-1-1 különbség osztható p-vel. Ezt röviden, kényelmesebben a kongruenciák nyelvén így írjuk:
| (2) | ap-1  1 (mod
p). 1 (mod
p). |
Például 212-1=4095 osztható 13-mal, azaz
212  1 (mod 13). Apja ösztönzésére megpróbálta bebizonyítani a
tétel fordítottját vagyis, ha (2) fennáll, abból következik, hogy
p prím. Ha a bizonyítás sikerrel jár, akkor ez a tétel
szolgáltatta volna a prímszámképletet. Bolyai azonban néhány kísérlet
után több olyan összetett számra bukkant, amelyekre (2) igaz. Azt
találta például, hogy
1 (mod 13). Apja ösztönzésére megpróbálta bebizonyítani a
tétel fordítottját vagyis, ha (2) fennáll, abból következik, hogy
p prím. Ha a bizonyítás sikerrel jár, akkor ez a tétel
szolgáltatta volna a prímszámképletet. Bolyai azonban néhány kísérlet
után több olyan összetett számra bukkant, amelyekre (2) igaz. Azt
találta például, hogy
2340  1 (mod 341),
1 (mod 341),
pedig 341=11 .31 és
414  1 (mod 15)
1 (mod 15)
holott 15=3 .5.
A kis Fermat tételt kielégítő összetett számokat pszeudoprímszámoknak, álprímeknek nevezzük. Bolyai tehát felfedezett több álprímet akkor, amikor az ő idejében még csak egy matematikus találta meg a 341-es számot. Erről azonban Bolyai nem tudott. Ezek az érdekes számok fontos szerephez jutottak a XX. században, a titkos üzenetküldések rejtjelezésében, a kriptográfiában [3], [4], [5].
A kis Fermat tételhez fűződő vizsgálódásai során jutott el Bolyai János a következő tétel bizonyításához: ha p és q prímszámok, az a egy olyan egész szám, amely nem osztható sem p-vel, sem q-val, akkor
apq-1  1 (mod
pq).
1 (mod
pq).
Ezzel a tétellel - amely csak most került elő a kéziratokból - több mint 40 évvel megelőzte J. H. Jeans (1877-1946) angol matematikust, aki először közölte azt nyomtatásban.
Ugyancsak Bolyai Farkas bíztatta fiát arra, hogy keresse meg a fent már említett Fermat karácsonyi tételének ,,legegyszerűbb'' bizonyítását. A tételt Fermat fogalmazta meg (1640 karácsonyán), de csak jóval később L. Euler (1707-1783) bizonyította be egy hosszú, 55 oldalas dolgozatban. Bolyai János - felhasználva a komplex egészek elméletét - négy bizonyítást is talált a tételre. Ezek közül az egyik különösen rövid és egyszerű. Mindössze két sor. A XX. század matematikusai valósággal versenyeztek azon, hogy ki tudna minél egyszerűbb bizonyítást találni Fermat tételére. Ezek a kísérletek Don Zagier 1990-es dolgozatában csúcsosodtak ki, amelyben ő ,,egy mondatban'' bizonyította be a tételt [11]. Sokan úgy gondolják, hogy ez a tételre adható legszebb bizonyítás, következésképpen ez ,,került be'' az Erdős Pál által oly sokszor emlegetett Nagy Könyvbe [10]. Véleményünk szerint a Nagy Könyvben nem Zagier, hanem Bolyai János bizonyítása található.
Érdekes színfoltja a Bolyai-iratoknak egy bűvös négyzet, amelyet a KöMaL olvasói már régebben megismerhettek [1], [8].
Bolyai még számos, korában újnak számító számelméleti feladattal foglalkozott és ért el figyelemre méltó eredményeket. Ezeket most nem részletezzük. Az érdeklődő olvasó megtalálja a [7], [9] munkákban.
Az algebrai egyenletek megoldhatóságáról
Az algebrai egyenletekkel kapcsolatban felmerülő legfontosabb feladat megoldásainak (gyökeinek) megkeresése. Valamely algebrai egyenlet algebrai megoldásán egy olyan eljárást értünk, amely az egyenlet gyökeit annak együtthatóiból kizárólag a négy alapművelet, a hatványozás és pozitív egész kitevőjű gyökvonás véges sokszor való alkalmazásával adja meg. Ezt úgy is szoktuk mondani, hogy célunk egy általános gyökképlet megadása. Az első- és másodfokú egyenletek megoldóképleteit már a középiskolában megismerjük. Léteznek megoldási képletek - igaz jóval bonyolultabbak - a harmad- és negyedfokú egyenletekre is [2]. Ezeket a XVI. században találták meg olasz matematikusok. Az itáliai matematikusok sikerei után nem létezett egyetlen jelentős matematikus sem, aki ne próbálta volna megoldani az ötöd- és magasabb fokú egyenleteket. Erőfeszítéseik azonban sorra kudarcot vallottak, mégpedig azért, mert ezekre az egyenletekre általában nem létezik megoldóképlet. Erre először Paolo Ruffini (1765-1822) adott bizonyítást 1799-ben, amely azonban hiányos volt. Végül 1826-ban hibátlan bizonyításával Niels Abel (1802-1829) tisztázta a problémát.
Bolyai János nagy szenvedéllyel vizsgálta az algebrai egyenletek megoldhatóságának kérdését. Feljegyzéseiből kiolvashatjuk, hogy hosszú ideig ő is az ötödfokú algebrai egyenlet megoldásán fáradozott, de később eljutott a Ruffini-Abel tételig. Marosvásárhelyen a Teleki Tékában megtalálta Andreas von Ettingshausen (1796-1887) algebra tankönyvét, amelyben a szerző közli Ruffini hibás bizonyítását. Bolyai észrevette ezt a hibát, kijavította azt, és ezáltal meggyőződött, hogy a négynél magasabb fokú algebrai egyenletek algebrai úton általában nem oldhatók meg. Meg kell jegyeznünk, hogy ez már Abel dolgozatának megjelenése után történt. Bolyai azonban sem erről, sem másik kortársa Evariste Galoisnak (1811-1832) az algebrai egyenletek elméletével kapcsolatos munkásságáról nem értesült. Ám a matematikatörténet sem tudott arról, hogy a XIX. század közepén a magyar matematikának is volt egy olyan tudósa, aki megoldotta az algebra 300 éves problémáját.
Bolyai Jánost az abszolút geometria felfedezőjeként tiszteli a világ. Felismerte az euklidészi párhuzamossági axiómának a többi axiómától való függetlenséget, amivel egy kétezeréves fejlődései periódust zárt le. Ezért több mint egy évszázadon át Bolyai munkásságát az Appendix-szel azonosították. Az utóbbi évek kutatásai nyomán azonban kiderült, hogy a matematika más ágaiban is figyelemre méltó eredményeket ért el. Most, születésének 200. évfordulóján szükséges feleleveníteni életútját, gondolatait, matematikai munkásságát a legfrissebb kutatási eredmények felhasználásával. Ezáltal a geometria nagy felfedezőjének egy árnyaltabb, színesebb, teljesebb portréja rajzolódik ki előttünk.
Irodalom
[1] Berger György, Megjegyzés a Gy. 3278. feladathoz, KöMaL, 49, 1999/9. szám, 534. old.
[2] Csete Lajos, Niccolo Fontana (más néven Tartaglia) számolómester egy verseny feladatáról, KöMaL, 51, 2001/5. szám, 267-274. old.
[3] Dénes József, Gondolatok a rejtjelezés megfejthetőségéről, Híradástechnika, 56, 2001/7. szám, 21-25. old.
[4] Dénes Tamás, Pierre Fermat és a nyilvános kulcsú rejtjelzés, KöMaL, 51, 2001/8. szám, 450-459. old.
[5] Járási István, A Carmichael-számokról, KöMaL, 50, 2003/3. szám, 136-145. old.
[6] Hraskó András, Pontok és nézőpontok - megjegyzések egy Kürschák feladathoz, KöMaL, 51, 2001/3. szám, 140-146. old.
[7] Kiss Elemér, Matematikai kincsek Bolyai János kéziratos hagyatékából, Akadémiai Kiadó, Typotex Kft., Budapest, 1999.
[8] Kiss Elemér, János Bolyai the First Hungarian Number Theorist, KöMaL Special english language issue 1996, 8-10. old.
[9] Kiss Elemér, Sándor József, Bolyai János aritmetikai feladata, MatLap, Kolozsvár, 5, 2001/9. szám, 321-325.
[10] Kosztolányi J., Makay G., Pintér K., Pintér L., Matematikai problémakalauz I, Polygon Könyvtár, Szeged, 1999, 268-269. old., 6.17. probléma.
[11] Pataki János, Egy meglepő bizonyítás, KöMaL, 49, 1999/8. szám, 449-451. old.
[12] Prékopa András, Bolyai János forradalma, Természet Világa, 133, 7. szám, 290-295. old., 8. szám, 347-352. old., 9. szám.

