Az A. 407. feladat (2006. október)

A. 407. Az ABCDE négyoldalú gúlában az ACE sík 45^o-os szöget zár be az ABCD, ABE, BCE, CDE és DAE lapok mindegyikével. Igazoljuk, hogy AB²+AD²=BC²+CD².

(5 pont)

A beküldési határidő 2006. november 15-én LEJÁRT.

Megoldás. Jelöljük a B és a D pontok merőleges vetületét az ACE síkon B'-vel, illetve D'-vel. Mivel az ABC, ABE és BCE síkok egyaránt 45^o-os szöget zárnak be az ACE síkkal, a B' pont távolsága az AC, AE és CE egyenesek mindegyikétől éppen BB', függetlenül attól, hogy B' az egyeneseknek melyik oldalára esik. Hasonlóképpen, a a D' pont távolsága az AC, AE és CE egyenesek mindegyikétől éppen DD' (1. ábra).

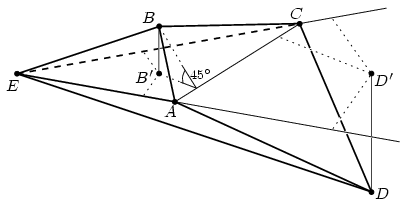
1. ábra

Négy olyan pont van az ACE háromszög síkjában, ami egyenlő távolságra van az AC, AE, CE egyenesektől; a háromszög beírt körének, valamint a három hozzáírt körének középpontja. Jelölje ezeket I, illetve a szokásos indexeléssel I_A, I_C és I_E; a B' és a D' pont ezek közül kettő.

Mivel az ABE és az ADE síkok, illetve a BCE sík és a CDE síkok szimmetrikusak az ACE síkra, az AB és az AD egyenesek is egymás tükörképei. Az AB és AD egyenesek merőleges vetülete az ACE síkra tehát egybeesik; a B' és D' pont az AEC szögnek ugyanazon a (belső vagy külső) szögfelezőjén van.

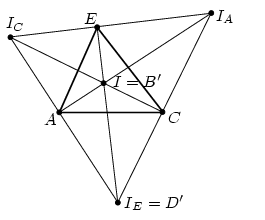
2. ábra

Ha B' és D' az AEC szög belső szögfelezőjén van, akkor egyikük I, a másik I_E. Mivel B és D szerepe felcserélhető, feltehetjük, hogy B'=I és D'=I_E (2. ábra). A Pitagorasz-tételt felírva az ABB', ADD' és AB'D' derékszögű háromszögekre,

AB²+AD²=(AB'²+BB'²)+(AD'²+DD'²)=

=(AB'²+AD'²)+BB'²+DD'²=B'D'²+BB'²+DD'².

Hasonlóan, az A helyére C-t írva,

BC²+CD²=(B'C²+BB'²)+(CD'²+DD'²)=

=(B'C²+CD'²)+BB'²+DD'²=B'D'²+BB'²+DD'².

Azt kaptuk, hogy AB²+AD²=BC²+CD², az állítás tehát teljesül.

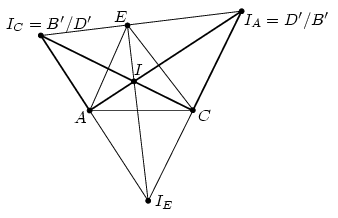
3. ábra

Most vizsgáljuk azt az esetet, amikor B' és D' az AEC szög külső szögfelezőjén van, vagyis egyikük I_A, a másik I_C. Az AB'CD' négyszög, ami a gúla ABCD alaplapjának merőleges vetülete az ACE síkra, mindkét esetben hurkolt (3. ábra), ami ellentmondás. Ez az eset tehát nem lehetséges.

Megjegyzések. 1. A bizonyítandó egyenlőség a hurkolt esetben is teljesül.

2. A versenyzők többsége indoklás nélkül feltételezte, hogy a gúla konvex, és nem vizsgálta azt az esetet, amikor az ACE háromszög két oldallappal is 135^o-os szöget zár be. (Ez az oka a sok 4 pontos dolgozatnak.) Ha az ACE sík mindegyik oldallappal ugyanakkora szöget zár be, akkor a konkáv eset valóban nem lehetséges (csak a hurkolt), de ez mindenképpen indoklásra szorul.

Statisztika:

15 dolgozat érkezett.
4 pontot kapott:	Bogár 560 Péter, Bohus Péter, Gyenizse Gergő, Hujter Bálint, Kisfaludi-Bak Sándor, Kónya 495 Gábor, Korándi Dániel, Kornis Kristóf, Lovász László Miklós, Nagy 224 Csaba, Nagy 235 János, Nagy 314 Dániel, Sümegi Károly, Tomon István.
0 pontot kapott:	1 versenyző.

A KöMaL 2006. októberi matematika feladatai