Az A. 568. feladat (2012. szeptember)

A. 568. Adott az ABC háromszög, és a beírt körének középpontján átmenő egyenes. Jelölje A', B', illetve C' az A, a B, illetve a C pont -re vonatkozó tükörképét. Legyen az A', B' és C' pontokon át -lel húzott párhuzamosok metszéspontja a BC, CA és AB egyenesekkel rendre P, Q, illetve R. Bizonyítsuk be, hogy a P, Q, R pontok egy egyenesen vannak, és ez az egyenes érinti a beírt kört.

(5 pont)

A beküldési határidő 2012. október 10-én LEJÁRT.

Megoldásvázlat. Mivel az egyenes átmegy a beírt kör középpontján, az A'B', B'C', C'A' egyenesek is érintik a beírt kört. Rajzoljuk meg a P ponton át a beírt kör másik, B'C'-től különböző érintőjét is; messe ez az érintő a CA és AB egyeneseket a Q^*, illetve az R^* pontban. Azt akarjuk megmutatni, hogy Q^*=Q és R^*=R.

Legyen I az egyenes ideális pontja. Legyen U az , a BC és a B'C' egyenesek közös pontja, V az , a CA és a C'A' egyenesek közös pontja, és W az , a AB és a A'B' egyenesek közös pontja. (Mivel az A',B',C' pontok az A,B,C pontok -re vontakozó tükörképei, ezek a pontok valóban léteznek.)

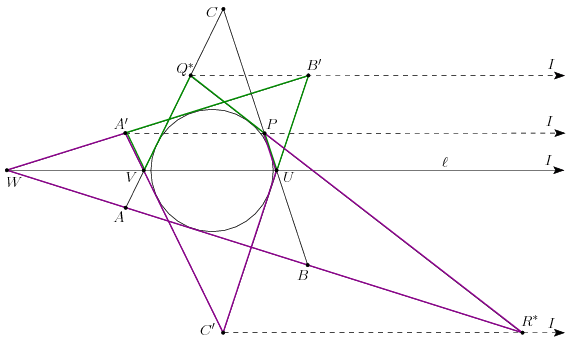
Alkalmazzuk a Brianchon-tételt a A'VQ^*PUB' hurkolt hatszögre, amelynek oldalegyenesei érintik a beírt kört. A tétel szerint a hatszög A'P, VU és Q^*B' átlóegyenesei egy ponton mennek át. Mivel A'P és VU= párhuzamos, a közös pont I, vagyis Q^*B' is párhuzmos -el. Ugyanakkor a az A'C' egyenesnek Q az a pontja, amire QB' párhuzmos -el. Tehát Q^*=Q.

Hasonlóan, a Brianchon-tételt az A'WR^*PUC' érintőhatszögre alkalmazva láthatjuk, hogy R^*C' is prhuzamos -el, következésképpen R^*=R.

Megjegyzés. Vannak olyan elfajuló esetek, amikor a megoldás nem mondható el ebben a formában; például ha valamelyik csúcs az egyenesre esik, vagy valamelyik oldal merőleges -re. Az ilyen eseteket külön meg kell vizsgálnunk, vagy pedig az általános eset határeseteiként kell előállítanunk.

Statisztika:

7 dolgozat érkezett.
5 pontot kapott:	Herczeg József, Ioan Laurentiu Ploscaru, Janzer Olivér, Nagy Róbert, Szabó 928 Attila.
2 pontot kapott:	2 versenyző.

A KöMaL 2012. szeptemberi matematika feladatai