Az A. 579. feladat (2013. január)

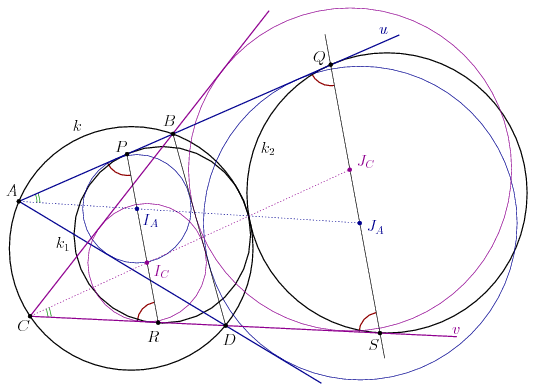
A. 579. A k₁ kör belülről érinti a k kört, ami kívülről érinti a k₂ kört. A k₁ és k₂ külső közös érintői u és v. Az u egyenes k₁-et a P, k₂-t a Q pontban érinti, a k kört pedig A-ban és B-ben metszi úgy, hogy a B metszéspont esik a PQ szakaszra. Hasonlóan, a v egyenes k₁-et az R, k₂-t az S pontban érinti, k-t pedig C-ban és D-ben metszi úgy, hogy a D pont esik az RS szakaszra, és k₁ az A-t és C-t nem tartalmazó BD ívet érinti.

Mutassuk meg, hogy

$\frac {AB\cdot AD} {AP\cdot AQ} = \frac {CB\cdot CD} {CR\cdot CS} .$

(5 pont)

A beküldési határidő 2013. február 11-én LEJÁRT.

Megoldásvázlat. Legyen az ABD és CBD háromszögek beírt köreinek középpontja I_A, illetve I_C, továbbá legyen ugyanezekben a háromszögekben a BD oldalhoz hozzáírt körök középpontja J_A, illetve I_C.

Lemma. A PR szakasz átmegy az I_A és I_C pontokon, továbbá a QS egyenes átmegy a J_A és J_C pontokon.

A lemma első fele (a beírt körökre vonatkozó állítás) Sawayama-lemma néven ismert. Egy-egy bizonyítása megtalálható például az A. 505. feladat megoldásában vagy itt vagy itt. Az Olvasóra bízzuk annak végiggondolását, hogy a bizonyításokat hogyan lehet átírni hozzáírt körökre.

Jól ismert (és például az ABI_A és AJ_AD háromszögek hasonlóságából könnyen igazolható), hogy

AB^.AD=AI_A^.AJ_A,

és ugyanígy

CB^.CD=CI_C^.CJ_C.

Az AI_AP, AJ_AQ, CI_CR és CJ_CS háromszögek hasonlók, mert PR és QS párhuzamos. Ezért

$\dfrac{AI_A}{AP} = \dfrac{AJ_A}{AQ} =\dfrac{CI_C}{CR} = \dfrac{CJ_C}{CS}.$

Így

$\dfrac{AB\cdot AD}{AP\cdot AQ} = \dfrac{AI_A\cdot AJ_A}{AP\cdot AQ} = \dfrac{AI_A}{AP}\cdot\dfrac{AJ_A}{AQ} = \dfrac{CI_C}{CR}\cdot\dfrac{CJ_C}{CS} = \dfrac{CI_C\cdot CJ_C}{CR\cdot CS} = \dfrac{CB\cdot CD}{CR\cdot CS}.$

Statisztika:

2 dolgozat érkezett.

5 pontot kapott: Cyril Letrouit.

3 pontot kapott: 1 versenyző.

A KöMaL 2013. januári matematika feladatai

2 dolgozat érkezett.
5 pontot kapott:	Cyril Letrouit.
3 pontot kapott:	1 versenyző.

Már regisztráltál?
Új vendég vagy?