 |
Az A. 629. feladat (2014. december) |
A. 629. A négyzetrácson megjelöltünk végtelen sok rácspontot úgy, hogy egyetlen körvonalon sincs 2014-nél több a megjelölt pontok közül. Mutassuk meg, hogy biztosan van olyan \(\displaystyle 100\) egység átmérőjű körlap (a négyzetrács síkjában), amelynek belsejében nincs egyetlen megjelölt pont sem.
Javasolta: Ágoston Péter, Gyenes Zoltán és Hujter Bálint
(5 pont)
A beküldési határidő 2015. január 12-én LEJÁRT.
Megoldás. A koordinátarendszer kezdőpontját jelölje \(\displaystyle O\). A rácspontokat azonosítjuk az \(\displaystyle O\)-ból induló helyvektoraikkal; így tetszőleges \(\displaystyle A,B\) pontokra értelmezzük pontok összegét is: \(\displaystyle A+B\) az a pont, ahova az \(\displaystyle \vec{OA}+\vec{OB}\) vektor mutat. A sík bármely \(\displaystyle \mathcal{H}\) halmazára és \(\displaystyle P\) pontra \(\displaystyle \mathcal{H}+P\) fogja jelölni a \(\displaystyle \mathcal{H}\) halmaz eltoltját az \(\displaystyle \vec{OP}\) vektorral: \(\displaystyle \mathcal{H}+P = \{X+P:X\in\mathcal{H}\}\).
Legyen \(\displaystyle \mathcal{D}\) az origó középpontú, \(\displaystyle 100\) sugarú körlap. A \(\displaystyle \mathcal{D}\) belsejébe eső rácspontok számát jelölje \(\displaystyle r\); maguk a körbe eső rácspontok legyenek \(\displaystyle X_1,X_2,\ldots,X_r\).
Legyen \(\displaystyle n=2014r+1\). Jól ismert, hogy van olyan körvonal, amely legalább \(\displaystyle n\) rácsponton átmegy. (Pl. az \(\displaystyle (n+i)^k(n-i)^{n-k}\) alakú komplex számok, ahol \(\displaystyle k=0,1,\ldots,n\), egy körön vannak és különbözők.) Vegyünk egy ilyen kört, és az origóból nagyítsuk a \(\displaystyle 201\)-szeresére. A felnagyított körvonalt jelöljük \(\displaystyle \mathcal{K}\)-val. A \(\displaystyle \mathcal{K}\) körön van legalább \(\displaystyle n\) (felnagyított) rácspont, \(\displaystyle P_1,P_2,\ldots,P_n\) úgy, hogy ezek közül bármely kettő távolsága nagyobb, mint \(\displaystyle 200\). Minden egyes \(\displaystyle k\)-ra Legyen \(\displaystyle \mathcal{D}_k=\mathcal{D}+P_k\) a \(\displaystyle P_k\) középpontú, \(\displaystyle 100\) sugarú körlap; ezek tehát páronként diszjunktak, mert középpontaik távolságai minden esetben nagyobbak \(\displaystyle 200\)-nál. Azt állítjuk, hogy a \(\displaystyle \mathcal{D}_1,\ldots,\mathcal{D}_n\) körlapok között van legalább egy, amelyik nem tartalmaz a belsejében megjelölt rácspontot.
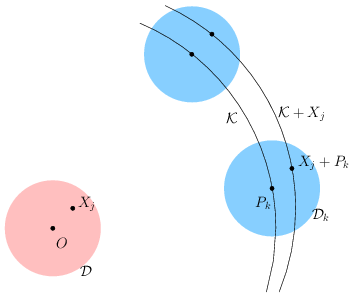
Minden egyes \(\displaystyle 1\le k\le n\)-re, a \(\displaystyle \mathcal{D}_k=\mathcal{D}+P_k\) körbe eső rácspontok \(\displaystyle X_1+P_j,\ldots,X_r+P_j\). A \(\displaystyle \mathcal{D}_1,\ldots,\mathcal{D}_n\) körlapok együttesen az \(\displaystyle X_j+P_k\) alakú rácspontokat (\(\displaystyle 1\le j\le r\), \(\displaystyle 1\le k\le n\)) tartalmazzák.
Mivel mindegyik \(\displaystyle P_k\) pont rajta van a \(\displaystyle \mathcal{K}\) körön, az \(\displaystyle X_j+P_k\) pont rajta van a \(\displaystyle \mathcal{K}+X_j\) körön. Vagyis, a \(\displaystyle \mathcal{K}+X_1, \ldots, \mathcal{K}+X_r\) körök együttesen az összes \(\displaystyle X_j+P_k\) alakú pontot tartalmazzák. A feltétel szerint minden körvonal, így a \(\displaystyle \mathcal{K}+X_1, \ldots, \mathcal{K}+X_r\) körvonalak mindegyike legfeljebb \(\displaystyle 2014\) megjelölt pontot tartalmaz; ez összesen legfeljebb \(\displaystyle r\cdot 2014\) megjelölt pont. Mivel \(\displaystyle n>2014r\), és a \(\displaystyle \mathcal{D}_j\) körlapok diszjunktak, a skatulya-elv miatt nem tartalmazhat mindegyik \(\displaystyle \mathcal{D}_j\) körlap megjelölt pontot.
Statisztika:
6 dolgozat érkezett. 5 pontot kapott: Fehér Zsombor, Janzer Barnabás, Szabó 789 Barnabás, Williams Kada. 4 pontot kapott: Gáspár Attila. 0 pontot kapott: 1 versenyző.
A KöMaL 2014. decemberi matematika feladatai
