Az A. 636. feladat (2015. február)

A. 636. Adott egy konvex \(\displaystyle ABCD\) négyszög és a \(\displaystyle BCD\) háromszög belsejében egy \(\displaystyle P\) pont úgy, hogy az \(\displaystyle ABPD\) négyszög érintőnégyszög, továbbá az \(\displaystyle ABPD\) négyszög beírt köre, a \(\displaystyle BCP\) háromszög beírt köre és a \(\displaystyle CDP\) háromszög beírt köre páronként érintik egymást. Jelölje \(\displaystyle Q\) és \(\displaystyle R\) a megfelelő körök érintési pontjait a \(\displaystyle BP\), illetve a \(\displaystyle DP\) szakaszon. Legyen \(\displaystyle S\) a \(\displaystyle BP\) és az \(\displaystyle AR\) egyenesek metszéspontja, \(\displaystyle T\) a \(\displaystyle DP\) és az \(\displaystyle AQ\) egyenesek metszéspontja, végül \(\displaystyle U\) a \(\displaystyle BT\) és a \(\displaystyle DS\) egyenesek metszéspontja. Mutassuk meg, hogy a \(\displaystyle CU\) egyenes felezi a \(\displaystyle BCD\) szöget.

(5 pont)

A beküldési határidő 2015. március 10-én LEJÁRT.

Megoldásvázlat.

Lemma. Tegyük fel, hogy az \(\displaystyle \omega_1\) és \(\displaystyle \omega_2\) körök az \(\displaystyle X\) pontban kívülről érinti egymást, és legyen \(\displaystyle Y\) és \(\displaystyle Z\) az \(\displaystyle X\)-ben húzott \(\displaystyle t_0\) érintő egyenes két pontja úgy, hogy \(\displaystyle X\) az \(\displaystyle YZ\) szakasz belsejébe esik. Húzzuk meg az \(\displaystyle Y\) és \(\displaystyle Z\) pontból a többi érintőt (\(\displaystyle t_1,t_2,t_3,t_4\)) a két körhöz. Létezik egy olyan \(\displaystyle \Omega\) kör, ami érinti a \(\displaystyle t_1,t_2,t_3,t_4\) egyeneseket úgy, hogy \(\displaystyle \Omega\) az \(\displaystyle t_1,t_2,t_3,t_4\) egyeneseknek \(\displaystyle X\)-szel azonos oldalára esik.

Bizonyítás Az \(\displaystyle t_1,t_2,t_3,t_4\) helyzetétől függően többféle eset is lehetséges. Most csak a baloldali ábra esetére írjuk le a bizonyítást; a többi eset hasonlóan kezelhető.

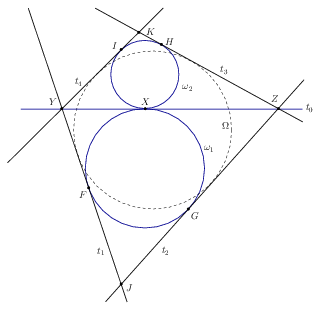
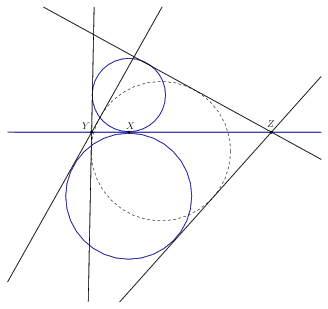
Betűzzük az érintési pontokat és az érintő egyenesek metszéspontjait az ábra szerint. Mivel \(\displaystyle YF=YX=XI\), \(\displaystyle ZG=ZX=ZH\), \(\displaystyle JF=JG\) és \(\displaystyle KH=KI\), az \(\displaystyle YJZK\) négyszögben \(\displaystyle YJ+ZK=JZ+KY\), így \(\displaystyle YJZK\) érintőnégyszög. A többi esetben a bizonyítás hasonló.

Térjünk most rá a feladat megoldására. Szintén a köröket érintő szakaszok összeszámolásából láthatjuk, hogy \(\displaystyle AB+CD=BC+DA\), így \(\displaystyle ABCD\) is érintőnégyszög. A Lemma fényében már négy kört is láthatunk, ami az ábrának négy-négy egyenesét érinti. Jelöljük az összesen hét érintő kört \(\displaystyle k_0,\ldots,k_6\)-tal az ábra szerint. Ezekre többször alkalmazni fogjuk a három hasonlósági pont tételét.

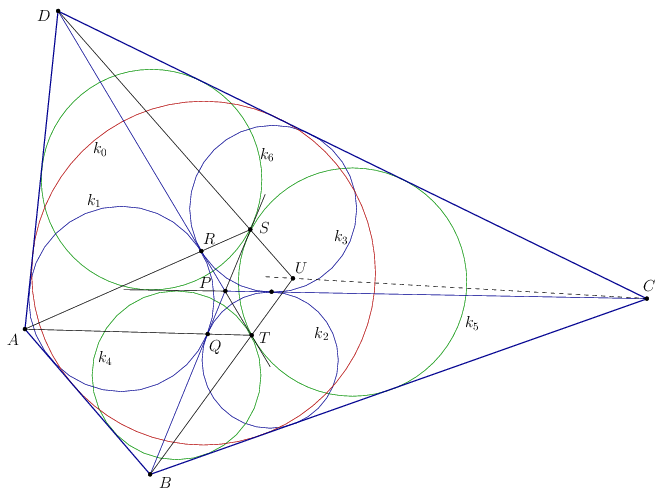
A \(\displaystyle k_0\) és a \(\displaystyle k_1\) külső hasonlósági pontja az \(\displaystyle A\) pont; a \(\displaystyle k_1\) és \(\displaystyle k_2\) belső hasonlósági pontja \(\displaystyle Q\), ezért az \(\displaystyle AQ\) egyenes átmegy \(\displaystyle k_0\) és \(\displaystyle k_2\) belső hasonlósági pontján. Hasonlóan, a \(\displaystyle k_0\) és a \(\displaystyle k_6\) külső hasonlósági pontja \(\displaystyle D\); a \(\displaystyle k_6\) és \(\displaystyle k_2\) belső hasonlósági pontja \(\displaystyle P\), ezért a \(\displaystyle DP\) egyenes is átmegy \(\displaystyle k_0\) és \(\displaystyle k_2\) belső hasonlósági pontján. Tehát, \(\displaystyle T=AQ\cap DP\) a \(\displaystyle k_0\) és \(\displaystyle k_2\) körök belső hasonlósági pontja.

Ugyanígy láthatjuk, hogy \(\displaystyle S\) a \(\displaystyle k_0\) és \(\displaystyle k_3\) körök belső hasonlósági pontja.

A \(\displaystyle k_0\) és a \(\displaystyle k_2\) belső hasonlósági pontja, mint láttuk, \(\displaystyle T\). A \(\displaystyle k_2\) és a \(\displaystyle k_5\) külső hasonlósági \(\displaystyle B\). Ezért a \(\displaystyle BT\) egyenes átmegy a \(\displaystyle k_0\) és a \(\displaystyle k_5\) belső hasonlósági pontján. Hasonlóan,a \(\displaystyle DS\) egyenes is átmegy a \(\displaystyle k_0\) és a \(\displaystyle k_5\) belső hasonlósági pontján. Így \(\displaystyle U=BT\cap DS\) a \(\displaystyle k_0\) és a \(\displaystyle k_5\) belső hasonlósági pontja.

Az \(\displaystyle k_0\) és a \(\displaystyle k_5\) belső hasonlósági pontja, \(\displaystyle U\) a két kör centrálisán van, ami éppen a \(\displaystyle BCD\) szög szögfelezője.

Statisztika:

2 dolgozat érkezett.
5 pontot kapott:	Janzer Barnabás.
1 pontot kapott:	1 versenyző.

A KöMaL 2015. februári matematika feladatai