 |
Az A. 655. feladat (2015. november) |
A. 655. A \(\displaystyle k_1\) és \(\displaystyle k_2\) körök az \(\displaystyle A\) és a \(\displaystyle B\) pontokban metszik egymást. A \(\displaystyle C\) és \(\displaystyle D\) pontok a \(\displaystyle k_1\), az \(\displaystyle E\) és \(\displaystyle F\) pontok pedig a \(\displaystyle k_2\) körön helyezkednek el úgy, hogy \(\displaystyle A\), \(\displaystyle C\), \(\displaystyle E\), illetve \(\displaystyle B\), \(\displaystyle D\), \(\displaystyle F\) kollineáris. Az \(\displaystyle ACE\) egyenesen \(\displaystyle G\), a \(\displaystyle BDF\) egyenesen \(\displaystyle H\) egy újabb pont. A \(\displaystyle CH\) egyenes az \(\displaystyle FG\) egyenest \(\displaystyle I\)-ben, a \(\displaystyle k_1\) kört másodszor \(\displaystyle J\)-ben metszi. A \(\displaystyle DG\) egyenes az \(\displaystyle EH\) egyenest \(\displaystyle K\)-ban, a \(\displaystyle k_1\) kört másodszor \(\displaystyle L\)-ben metszi. A \(\displaystyle k_2\) kör az \(\displaystyle EHK\) és \(\displaystyle FGI\) egyeneseket másodszor az \(\displaystyle M\), illetve az \(\displaystyle N\) pontban metszi. Az \(\displaystyle A,B,C,\ldots,N\) pontok különbözők. Mutassuk meg, hogy \(\displaystyle I\), \(\displaystyle J\), \(\displaystyle K\), \(\displaystyle L\), \(\displaystyle M\) és \(\displaystyle N\) egy körön vagy egy egyenesen vannak.
(5 pont)
A beküldési határidő 2015. december 10-én LEJÁRT.
Megoldás. A diszkusszió elkerülése éredekében a megoldás során végig irányított (modulo \(\displaystyle 180^\circ\)) szögekkel fogunk számolni.
A \(\displaystyle k_1\), \(\displaystyle k_2\) körökben alkalmazva a kerületi szögek tételét, láthatjuk, hogy az ábrán kék színnel jelölt szögek egyenlők:
\(\displaystyle ACD\angle = ALD\angle = ABD\angle = ABF\angle = ANF\angle = AEF\angle. \)
Mivel \(\displaystyle ANG\angle=ANF\angle=ALD\angle=ALG\angle\), az \(\displaystyle A,G,L,N\) pontok egy körön vagy egy egyenesen vannak. Egy egyenesen viszont nem lehetnek, mert például az \(\displaystyle A,L,D\) pontok különböző pontjai a \(\displaystyle k_1\) körnek, így \(\displaystyle ALD\angle\ne0\). Az \(\displaystyle A,G,L,N\) pontok tehát egy körön vannak. Hasonlóan, az \(\displaystyle A,C,E,G,L,N\) pontok és a \(\displaystyle B,D,E,H,J,M\) pontok szerepének felcserélésével láthatjuk, hogy a \(\displaystyle B,H,J,M\) pontok is egy körön vannak.
Mivel \(\displaystyle ECD\angle=ACD\angle=AEF\angle=CEF\angle\), a \(\displaystyle CE\) egyenes ugyanakkora irányított szöget zár be a \(\displaystyle CD\) és az \(\displaystyle EF\) egyenesekkel, így az \(\displaystyle CD\) és \(\displaystyle EF\) egyenesek párhuzamosak egymással.
Alkalmazzuk most a Papposz-tételt az egy egyenesre eső \(\displaystyle (C,G,E)\) és \(\displaystyle (F,H,D)\) ponthármasokra. A tétel szerint az \(\displaystyle CH\cap GF=I\) pont, a \(\displaystyle GD\cap EH=K\) pont, továbbá a \(\displaystyle CD\) és \(\displaystyle EF\) egyenesek meszéspontja egy egyenesre esik. Mivel azonban \(\displaystyle CD\|EF\), ez a metszéspont a projektív sík ideális egyenesén jön létre, így az \(\displaystyle IK\) egyenes is párhuzamos \(\displaystyle CD\)-vel.
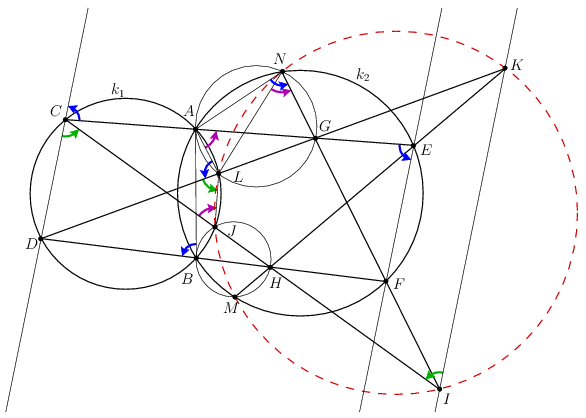
A \(\displaystyle CD\) és \(\displaystyle IK\) egyesek párhuzamossága és a \(\displaystyle k_1\) körre eső \(\displaystyle C,D,J,L\) pontok miatt a zöld színnel jelölt szögek is egyenlők:
\(\displaystyle KIJ\angle = KIC\angle = DCI\angle = DCJ\angle = DLJ\angle = KLJ\angle, \)
így az \(\displaystyle I,J,K,L\) pontok egy körön vagy egy egyenesen vannak. Mivel azonban \(\displaystyle KLJ\angle=DLJ\angle\ne0\), egy egyenesen nem lehetnek. Tehát \(\displaystyle I,J,K,L\) pontok egy körön vannak.
A lila szögek is egyenlők:
\(\displaystyle LNI\angle = LNG\angle = LAG\angle = LAC\angle = LJC\angle = LJI\angle. \)
Ebből következik, hogy \(\displaystyle N\) is rajta van az \(\displaystyle I,J,L\) pontok által egyértelműen meghatározott \(\displaystyle IJKL\) körön.
Ismét az \(\displaystyle A,C,E,H,K,L,N\) pontok és a \(\displaystyle B,D,F,G,I,J,M\) szerepének felcserélésével kapjuk, hogy az \(\displaystyle M\) pont is rajta van az \(\displaystyle IJKL\) körön.
Ezzel bebizonyítottuk, hogy az \(\displaystyle I,J,K,L,M,N\) pontok minden esetben egy körön vannak.
Statisztika:
9 dolgozat érkezett. 5 pontot kapott: Baran Zsuzsanna, Cseh Kristóf, Gáspár Attila, Lajkó Kálmán, Williams Kada. 4 pontot kapott: Bukva Balázs. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2015. novemberi matematika feladatai
