 |
Az A. 662. feladat (2016. február) |
A. 662. Az \(\displaystyle A_1\), \(\displaystyle A_2\), \(\displaystyle A_3\), \(\displaystyle A_4\), \(\displaystyle B_1\), \(\displaystyle B_2\), \(\displaystyle B_3\), \(\displaystyle B_4\) pontok, ebben a sorrendben, egy parabolán vannak. Minden \(\displaystyle (i,j)\) pár esetén, amelyre \(\displaystyle 1\le i,j\le4\) és \(\displaystyle i\ne j\), jelölje \(\displaystyle r_{ij}\) azt az arányt, amelyben az \(\displaystyle A_jB_j\) egyenes kettéosztja az \(\displaystyle A_iB_i\) szakaszt. (Ha tehát \(\displaystyle A_iB_i\) és \(\displaystyle A_jB_j\) metszéspontja \(\displaystyle X\), akkor \(\displaystyle r_{ij}=\frac{A_iX}{XB_i}\).) Mutassuk meg, hogy ha az \(\displaystyle r_{12} \cdot r_{21} \cdot r_{34} \cdot r_{43}\), \(\displaystyle r_{13} \cdot r_{31} \cdot r_{24} \cdot r_{42}\) és \(\displaystyle r_{14} \cdot r_{41} \cdot r_{23} \cdot r_{32}\) számok közül közül valamelyik kettő megegyezik, akkor a harmadik is egyenlő velük.
(5 pont)
A beküldési határidő 2016. március 10-én LEJÁRT.
1. megoldás (vázlat). Helyezzük el a parabolát a derékszögű koordináta-rendszerben úgy, hogy az egyenlete \(\displaystyle y=x^2\) legyen. Legyen \(\displaystyle A_i=(a_i,a_i^2)\) és \(\displaystyle B_i=(b_i,b_i^2)\); feltehetjük, hogy \(\displaystyle a_1<a_2<a_3<a_4<b_1<b_2<b_3<b_4\).
Könnyű ellenőrizni, hogy bármely \(\displaystyle 1\le i,j\le 4\), \(\displaystyle i\ne j\) indexpárra az \(\displaystyle A_iB_i\) és \(\displaystyle A_jB_j\) szakaszok metszéspontja
\(\displaystyle \left( \frac{a_jb_j-a_ib_i}{a_j+b_j-a_i-b_i}; \frac{a_ia_jb_j-a_jb_ib_j-a_ia_jb_i-a_ib_ib_j}{a_j+b_j-a_i-b_i} \right) \)
és
\(\displaystyle r_{ij} = \frac{(a_j-a_i)(b_j-a_i)}{(b_i-a_j)(b_j-b_i)}. \)
Ezt behelyettesítve,
\(\displaystyle r_{12}r_{21}r_{34}r_{43} = \frac{(a_2-a_1)^2(a_4-a_3)^2}{(b_2-b_1)^2(b_4-b_3)^2}, \)
\(\displaystyle r_{13}r_{31}r_{24}r_{42} = \frac{(a_3-a_1)^2(a_4-a_2)^2}{(b_3-b_1)^2(b_4-b_2)^2}, \)
\(\displaystyle r_{14}r_{41}r_{23}r_{32} = \frac{(a_4-a_1)^2(a_3-a_2)^2}{(b_4-b_1)^2(b_3-b_2)^2} \)
avagy, gyököt vonva és a nevezőkkel átszorozva,
| \(\displaystyle (a_2-a_1)(a_4-a_3) = (b_2-b_1)(b_4-b_3) \cdot \sqrt{r_{12}r_{21}r_{34}r_{43}} \) | (1) |
| \(\displaystyle (a_3-a_1)(a_4-a_2) = (b_3-b_1)(b_4-b_2) \cdot \sqrt{r_{13}r_{31}r_{24}r_{42}} \) | (2) |
| \(\displaystyle (a_4-a_1)(a_3-a_2) = (b_4-b_1)(b_3-b_2) \cdot \sqrt{r_{14}r_{41}r_{23}r_{32}} \) | (3) |
Vegyük észre, hogy
\(\displaystyle (a_2-a_1)(a_4-a_3) + (a_4-a_1)(a_3-a_2) = (a_3-a_1)(a_4-a_2), \)
és hasonlóan,
\(\displaystyle (b_2-b_1)(b_4-b_3) + (b_4-b_1)(b_3-b_2) = (b_3-b_1)(b_4-b_2). \)
vagyis, ha a jobboldalakon a három négyzetgyök egyenlő egymással, akor (1) és (3) összege éppen (2)-t adja.
Ha \(\displaystyle r_{12}r_{21}r_{34}r_{43}=r_{14}r_{41}r_{23}r_{32}\), akkor (1) és (3) összegét (2)-vel összehasonlítva látjuk, hogy \(\displaystyle r_{13}r_{31}r_{24}r_{42}\) is ugyanakkora. Ha \(\displaystyle r_{12}r_{21}r_{34}r_{43}=r_{13}r_{31}r_{24}r_{42}\), akkor (2) és (1) különbségét vetjük össze (3)-mal; ha pedig \(\displaystyle r_{13}r_{31}r_{24}r_{42}=r_{14}r_{41}r_{23}r_{32}\), akkor (2) és (3) különbségét hasonlítjuk össze (1)-gyel.
2. megoldás. Parabola helyett valójában bármilyen nem elfajuló kúpszelettel igaz az állítás. A megoldás első lépéseként visszavezetjük az állítást a kör esetére.
Helyezzük el a parabolát egy forgáskúp palástján, és a kúp csúcsábül vetítsük az ábrát egy, a kúp tengelyére merőleges síkra; így a parabola képe egy \(\displaystyle k\) kör lesz. Legyen az \(\displaystyle A_i\) pont képe \(\displaystyle C_i\), a \(\displaystyle B_i\) képe \(\displaystyle D_i\). Legyen minden \(\displaystyle i\ne j\) indexpárra \(\displaystyle X_{ij} = A_iB_i \cap A_jB_j\); ennek vetített képe az \(\displaystyle Y_{ij} = C_iD_i \cap C_jD_j\) pont. Az \(\displaystyle X_{ij}\) és \(\displaystyle Y_{ij}\) pontok jelölésében a két index szerepe szimmetrikus, így \(\displaystyle X_{ji}=X_{ij}\) és \(\displaystyle Y_{ji}=Y_{ij}\). Az \(\displaystyle r_{ij}\) arányok mintájára legyen \(\displaystyle s_{ij}=\frac{C_iY_{ij}}{Y_{ij}D_i}\).
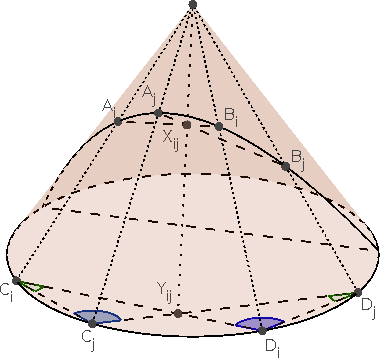
Vegyük észre, hogy tetszőleges \(\displaystyle i,j,k\), különböző indexekre
\(\displaystyle \frac{r_{ij}}{r_{ik}} = \frac{A_iX_{ij}}{X_{ij}B_i} : \frac{A_iX_{ik}}{X_{ik}B_i} = (A_i,B_i,X_{ij},X_{ik}). \)
Mivel a vetítés megtartja a kettősviszonyt,
\(\displaystyle \frac{r_{ij}}{r_{ik}} = (A_i,B_i,X_{ij},X_{ik}) = (C_i,D_i,Y_{ij},Y_{ik}) = \frac{C_iY_{ij}}{Y_{ij}D_i} : \frac{C_iY_{ik}}{Y_{ik}D_i} = \frac{s_{ij}}{s_{ik}}. \)
Ennek egyszerű következménye, hogy az \(\displaystyle r_{12}r_{21}r_{34}r_{43}\), \(\displaystyle r_{13}r_{31}r_{24}r_{42}\) és \(\displaystyle r_{14}r_{41}r_{23}r_{32}\) számok aránya ugyanaz, mint az \(\displaystyle s_{12}s_{21}s_{34}s_{43}\), \(\displaystyle s_{13}s_{31}s_{24}s_{42}\) és \(\displaystyle s_{14}s_{41}s_{23}s_{32}\) számok aránya. Például,
\(\displaystyle \frac{r_{12}r_{21}r_{34}r_{43}}{r_{13}r_{31}r_{24}r_{42}} = \frac{r_{12}}{r_{13}} \cdot \frac{r_{21}}{r_{24}} \cdot \frac{r_{34}}{r_{31}} \cdot \frac{r_{43}}{r_{42}} = \frac{s_{12}}{s_{13}} \cdot \frac{s_{21}}{s_{24}} \cdot \frac{s_{34}}{s_{31}} \cdot \frac{s_{43}}{s_{42}} = \frac{s_{12}s_{21}s_{34}s_{43}}{s_{13}s_{31}s_{24}s_{42}}. \)
(A másik két párra ez ugyanígy ellenőrizhető.)
A feladat állítása tehát ekvivalens a következővel:
|
A kerületi szögek tétele miatt a \(\displaystyle C_iC_jY_{ij}\) és \(\displaystyle D_jD_iY_{ij}\) háromszögek hasonlók, így
\(\displaystyle s_{ij}s_{ji} = \frac{C_iY_{ij}}{Y_{ij}D_i}\cdot \frac{C_jY_{ij}}{Y_{ij}D_j} = \frac{C_iY_{ij}}{Y_{ij}D_j}\cdot \frac{C_jY_{ij}}{Y_{ij}D_i} = \left(\frac{C_iC_j}{D_iD_j}\right)^2. \)
Ezt behelyettesítve,
\(\displaystyle s_{12}s_{21}s_{34}s_{43} = \left(\frac{C_1C_2\cdot C_3C_4}{D_1D_2\cdot D_3D_4}\right)^2; \quad s_{13}s_{31}s_{24}s_{42} = \left(\frac{C_1C_3\cdot C_2C_4}{D_1D_3\cdot D_2D_4}\right)^2; \quad s_{14}s_{41}s_{23}s_{32} = \left(\frac{C_1C_4\cdot C_2C_3}{D_1D_4\cdot D_2D_3}\right)^2. \)
Írjuk fel a Ptoleimaiosz-tételt az \(\displaystyle C_1C_2C_3C_4\) és \(\displaystyle D_1D_2D_3D_4\) húrnégyszögekre:
\(\displaystyle C_1C_2\cdot C_3C_4+C_1C_4\cdot C_2C_3 = C_1C_3\cdot C_2C_4; \quad D_1D_2\cdot D_3D_4+D_1D_4\cdot D_2D_3 = D_1D_3\cdot D_2D_4. \)
Ebből láthatjuk, hogy
\(\displaystyle \frac{ D_1D_2\cdot D_3D_4 \cdot \sqrt{s_{12}s_{21}s_{34}s_{43}} + D_1D_4\cdot D_2D_3 \cdot \sqrt{s_{14}s_{41}s_{23}s_{32}}}{ D_1D_2\cdot D_3D_4+D_1D_4\cdot D_2D_3} = \)
\(\displaystyle = \frac{C_1C_2\cdot C_3C_4+C_1C_4\cdot C_2C_3}{ D_1D_2\cdot D_3D_4+D_1D_4\cdot D_2D_3} = \frac{C_1C_4\cdot C_2C_3}{D_1D_4\cdot D_2D_3} = \sqrt{s_{13}s_{31}s_{24}s_{42}}; \)
máa szóval, a \(\displaystyle \sqrt{s_{12}s_{21}s_{34}s_{43}}\) és \(\displaystyle \sqrt{s_{14}s_{41}s_{23}s_{32}}\) számok súlyozott átlaga a \(\displaystyle D_1D_2\cdot D_3D_4\) és \(\displaystyle D_1D_4\cdot D_2D_3\) súlyokkal éppen \(\displaystyle \sqrt{s_{13}s_{31}s_{24}s_{42}}\). Ebből következik, hogy ha a három szám közül bármelyik kettő megegyezik, akkor a harmadik is egyenlő velük.
Statisztika:
5 dolgozat érkezett. 5 pontot kapott: Bodnár Levente, Bukva Balázs, Glasznova Maja, Imolay András, Williams Kada.
A KöMaL 2016. februári matematika feladatai
