Az A. 713. feladat (2018. január)

A. 713. Azt mondjuk, hogy a valós számokból álló \(\displaystyle a_1,a_2,\dots\) sorozat terpeszkedő, ha minden pozitív egész \(\displaystyle j\)-re \(\displaystyle i<j\) esetén \(\displaystyle |a_i-a_j|\ge \frac1{j}\). Határozzuk meg az összes olyan \(\displaystyle C\) pozitív valós számot, melyre megadható a \(\displaystyle [0;C]\) intervallumban egy terpeszkedő sorozat.

Javasolta: Di Giovanni Márk (Cambridge)

(5 pont)

A beküldési határidő 2018. február 12-én LEJÁRT.

Megoldás. Belátjuk, hogy pontosan akkor létezik \(\displaystyle [0;c]\)-ben terpeszkedő sorozat, hogyha \(\displaystyle c\ge 2\ln 2\).

1. Van sorozat \(\displaystyle \implies\) \(\displaystyle c\ge 2\ln 2\). Tekintsük az \(\displaystyle a_1,a_2,\dots,a_{2n+1}\) számokat! Következzenek egymás után

\(\displaystyle 0\le a_{i_1}<a_{i_2}<\dots<a_{i_{2n+1}}\le c\)

sorrendben. Ekkor felírhatjuk, hogy

\(\displaystyle c\ge \sum_{j=1}^{2n}|a_{i_{j+1}}-a_{i_j}|\ge \sum_{j=1}^{2n}\frac1{\max(i_j,i_{j+1})}\ge 2\left(\frac1{2n+1}+\frac1{2n}+\dots+\frac1{n+2}\right),\)

hiszen a \(\displaystyle \max(i_j,i_{j+1})\) sorozatban minden szám \(\displaystyle 1,2,\dots,2n+1\) közül legfeljebb kétszer fordulhat elő.

Mivel azonban

\(\displaystyle \ln 2=\ln(2n)-\ln n=\int_{n}^{2n}\frac1{x}dx<\frac1n+\frac1{n+1}+\dots+\frac1{2n-1},\)

ezért bármely \(\displaystyle \varepsilon>0\)-hoz létezik \(\displaystyle N\), melyre \(\displaystyle n\ge N\) esetén

\(\displaystyle 2\left(\frac1{2n+1}+\frac1{2n}+\dots+\frac1{n+2}\right)>2\ln 2-\varepsilon,\)

és így \(\displaystyle c<2\ln 2\) nem lehet, vagyis mindenképpen \(\displaystyle c\ge 2\ln 2\).

2. \(\displaystyle c\ge 2\ln 2\) \(\displaystyle \implies\) van sorozat. Konstruálunk egy terpeszkedő sorozatot a \(\displaystyle [0;2\ln 2]\) intervallumban. A könnyebb megértés végett előrevetítjük, hogy olyan fajta konstrukció ez, mely szemléletesen igen könnyen elképzelhető, ám nehezen írható le. A kulcsötlet, hogy "felfújjuk a sorozatot a \(\displaystyle [0;2\ln 2]\)-be, mint egy lufit". Vagyis míg egyre újabb tagokat veszünk hozzá a sorozathoz, a meglévő tagok közötti távolságokat kissé megnöveljük, hogy az új tagok elférjenek. A sorozat preciz módon történő megadásához véges sorozatok sorozatát készítjük el, majd határértéket veszünk.

Legyen \(\displaystyle t\ge 1\) esetén

\(\displaystyle S_t=2\left(\frac1{2^{t-1}+1}+\frac1{2^{t-1}+2}+\dots+\frac1{2^t}\right).\)

Mivel \(\displaystyle S_{t+1}\) úgy adódik \(\displaystyle S_t\)-ből, hogy minden \(\displaystyle \frac1{k}\) tag helyére \(\displaystyle \frac1{2k-1}+\frac1{2k}\) tagot írunk, így \(\displaystyle S_t<S_{t+1}\). Továbbá az

\(\displaystyle \ln 2-\frac1{2n+1}=-\frac1{2n+1}+\int_{n+1}^{2n+2}\frac1xdx<\frac1{n+1}+\frac1{n+2}+\dots+\frac1{2n}<\int_{n}^{2n}\frac1xdx=\ln 2\)

becslésből \(\displaystyle S_t\to 2\ln 2\) adódik. Ezért \(\displaystyle [0;S_t]\subset [0;2\ln 2]\).

Előbb megadjuk a sorozat tagjai közötti relációkat. Ehhez legyen \(\displaystyle b_1=0\) és \(\displaystyle b_2=\frac12\), majd pedig minden \(\displaystyle t\ge 2\)-re

\(\displaystyle b_{2^t}=\frac1{2^t},\quad b_{2^t-1}=\frac{3}{2^t},\quad \dots,\quad b_{2^{t-1}+1}=\frac{2^t-1}{2^t}.\)

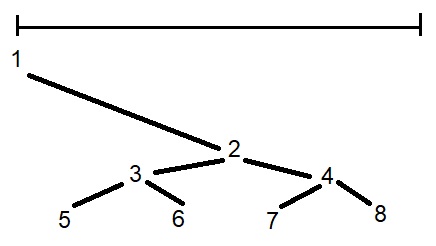
Következő lépésként minden \(\displaystyle t\ge 1\)-hez megadunk egy \(\displaystyle a_1(t),a_2(t),\dots,a_{2^t}(t)\) sorozatot a \(\displaystyle [0;S_t]\) intervallumban úgy, hogy \(\displaystyle a_i(t)<a_j(t)\) pontosan akkor, ha \(\displaystyle b_i<b_j\), és a sorozat tagjai növekvő sorrendben:

\(\displaystyle 0,\quad\frac1{2^t},\,\frac{2}{2^t},\quad \left(\frac{2}{2^t}+\frac1{2^t-1}\right),\,\left(\frac{2}{2^t}+\frac{2}{2^t-1}\right),\quad \left(\frac{2}{2^t}+\frac{2}{2^t-1}+\frac1{2^t-2}\right),\,\dots,\,S_t-\frac1{2^{t-1}+1}.\)

Mivel a felsorolásban a 2., 4., ..., \(\displaystyle 2^t\). szám éppen az \(\displaystyle a_{2^t}(t),a_{2^t-1}(t),\dots,a_{2^{t-1}+1}(t)\), ezért \(\displaystyle 2^{t-1}+1\le j\le 2^t\) esetén \(\displaystyle a_j(t)\) távolsága a szomszédos tagoktól is legalább \(\displaystyle \frac1j\).

Vegyük észre, hogy ha a \(\displaystyle t\)-edik sorozat két nagyság szerinti szomszédos tagjának különbsége \(\displaystyle \frac1k\), akkor az ugyanolyan indexszel rendelkező tagok különbsége a \(\displaystyle (t+1)\)-edik sorozatban \(\displaystyle \frac{2}{2k}\) vagy \(\displaystyle \frac{2}{2k-1}\) lesz. Ebből következik, hogy bármely \(\displaystyle i,j\)-re a \(\displaystyle t\mapsto |a_i(t)-a_j(t)|\) függvény monoton növekvő (elég nagy \(\displaystyle t\) értékeken), és így \(\displaystyle |a_i(t)-a_j(t)|\ge \frac1j\) minden (elég nagy) \(\displaystyle t\)-re, ha \(\displaystyle i<j\). Ezt speciálisan \(\displaystyle i=1\)-re véve azt is kapjuk, hogy (elég nagy \(\displaystyle t\) értékeken) \(\displaystyle t\mapsto a_j(t)\) monoton növekvő.

Befejezésül legyen az egyszerűség kedvéért \(\displaystyle a_i(t)=\frac1{2018}\), ha \(\displaystyle i>2^t\), és legyen \(\displaystyle i=1,2,\dots\)-ra

\(\displaystyle a_i:=\lim_{t\to\infty}a_i(t).\)

A határérték létezik, hisz \(\displaystyle t\mapsto a_i(t)\) monoton növekvő és felülről korlátos sorozat. Továbbá a \(\displaystyle [0;2\ln 2]\) intervallum zártsága miatt \(\displaystyle a_i\in[0;2\ln 2]\), és mivel \(\displaystyle i<j\) esetén \(\displaystyle |a_i(t)-a_j(t)|\ge \frac1j\) minden elég nagy \(\displaystyle t\)-re, ezért \(\displaystyle |a_i-a_j|<\frac1j\) nem állhat fenn.

Ezzel tehát konstruáltunk egy megfelelő terpeszkedő sorozatot a \(\displaystyle [0;c]\) intervallumban, ha \(\displaystyle c\ge 2\ln 2\).

Statisztika:

13 dolgozat érkezett.
5 pontot kapott:	Bukva Balázs, Daróczi Sándor, Gáspár Attila, Matolcsi Dávid, Schrettner Jakab.
4 pontot kapott:	Janzer Orsolya Lili, Schweitzer Ádám.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	2 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2018. januári matematika feladatai