Az A. 719. feladat (2018. március)

A. 719. Legyen \(\displaystyle ABC\) nem egyenlőszárú háromszög körülírt körének, illetve beírt körének középpontja \(\displaystyle O\), illetve \(\displaystyle I\). Az \(\displaystyle A\)-val szemköztes hozzáírt kör \(\displaystyle BC\)-t \(\displaystyle A_1\)-ben érinti, a \(\displaystyle B\)-vel szemköztes hozzáírt kör \(\displaystyle CA\)-t \(\displaystyle B_1\)-ben érinti, továbbá a \(\displaystyle C\)-vel szemköztes hozzáírt kör \(\displaystyle AB\)-t \(\displaystyle C_1\)-ben érinti. Legyen \(\displaystyle P\) az \(\displaystyle AB_1C_1\) háromszög magasságpontja, \(\displaystyle H\) pedig az \(\displaystyle ABC\) háromszög magasságpontja. Igazoljuk, hogy ha \(\displaystyle M\) a \(\displaystyle PA_1\) felezőpontja, akkor \(\displaystyle HM\) és \(\displaystyle OI\) párhuzamosak.

Javasolta: Michael Ren (Andover, Massachusetts, USA)

(5 pont)

A beküldési határidő 2018. április 10-én LEJÁRT.

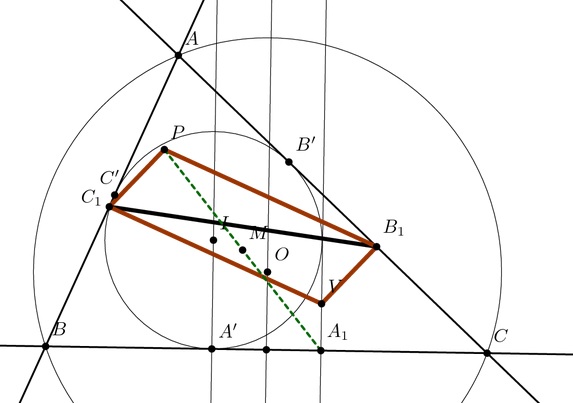
Megoldás. Az \(\displaystyle I\) pont vetülete \(\displaystyle BC,CA,AB\)-re legyen \(\displaystyle A',B',C'\) (ezek a beírt kör érintési pontjai). Ekkor ismert, hogy \(\displaystyle A'\) az \(\displaystyle A_1\) tükörképe \(\displaystyle BC\) felezőpontjára stb., amit abban foglalhatunk össze, hogy \(\displaystyle V\) pont vetülete \(\displaystyle BC,CA,AB\)-re \(\displaystyle A_1,B_1,C_1\), ahol \(\displaystyle V\) az \(\displaystyle I\) tükörképe \(\displaystyle O\)-ra.

A merőlegességek okán \(\displaystyle PB_1VC_1\) paralelogramma, vagyis \(\displaystyle P=B_1+C_1-V\) (ilyen jelölés esetén a pontokat helyvektoraikkal azonosítjuk). Innen

\(\displaystyle M=\frac12(A_1+B_1+C_1-V).\)

(Ez a szimmetria megsejthető, ha meglátjuk egy jó ábrán, hogy \(\displaystyle \overline{A_1P},\overline{B_1Q},\overline{C_1R}\) közös felezőpontban metsz, ahol \(\displaystyle P,Q,R\) az \(\displaystyle AB_1C_1,BC_1A_1,CA_1B_1\) magasságpontja.)

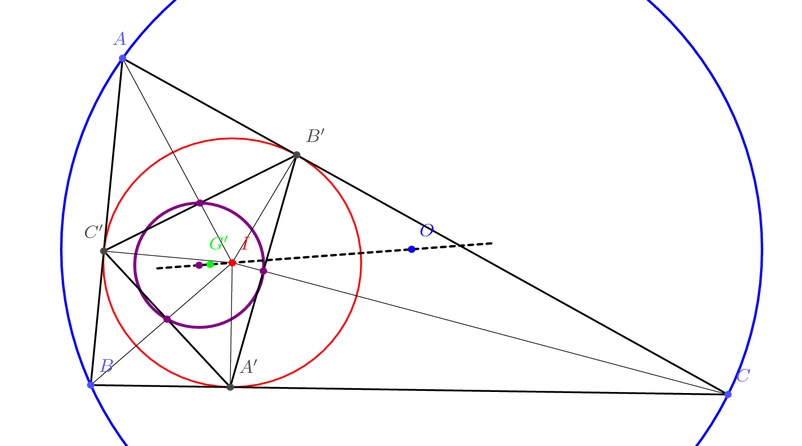
Ismert (a B.4773. feladat következménye, vagy adódik abból, hogy \(\displaystyle A'B'C'\) Feuerbach-körét a beírt körre invertálva, \(\displaystyle ABC\) körülírt körét kapjuk), hogy az \(\displaystyle A'B'C'\) háromszög \(\displaystyle G'\) súlypontja az \(\displaystyle IOV\) egyenes pontja:

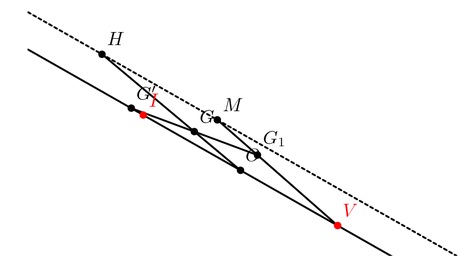
Ha \(\displaystyle G,G_1\) az \(\displaystyle ABC,A_1B_1C_1\) súlypontjai, akkor, mint kibontással ellenőrizhető, \(\displaystyle G=\frac12(G'+G_1)\). Ezért \(\displaystyle d(G_1,IO)=2d(G,IO)\), ahol \(\displaystyle d(\cdot,\cdot)\) jelöli két ponthalmaz minimális távolságát. Azonban \(\displaystyle H-O=3(G-O)\) (arányok Euler-egyenesen) és \(\displaystyle 2(M-V)=3(G_1-V)\) (fenti egyenlőség átrendezése), így

\(\displaystyle d(H,IO)=3\cdot d(G,IO)=\frac32\cdot d(G_1,IO)=d(M,IO),\)

tehát \(\displaystyle HM\) és \(\displaystyle IO\) párhuzamosak.

Megjegyzés. Érdemes meglátni e feladat laza kapcsolódását a B.4790. feladathoz, melyben a három egyenes \(\displaystyle O\)-ra való tükörképei az \(\displaystyle ABC\) magasságpontján haladnak át, mert a magasságpontnak a \(\displaystyle \overline{BC}\) felezőpontjára való tükörképe az \(\displaystyle ABC\) körön \(\displaystyle A\)-val átellenes pont.

Egy másik, ügyes számolást alkalmazó megközelítés, hogy a sík pontjait \(\displaystyle AB,AC\) számegyenesekre való \(\displaystyle u,v\) vetületeik szerint paraméterezzük. Ebben a koordináta-rendszerben levezetve adott irányú egyenes egyenletét, a feladatbeli pontok könnyen számolhatók \(\displaystyle ABC\) oldalainak segítségével (a koszinusztételt felhasználva).

Statisztika:

8 dolgozat érkezett.
5 pontot kapott:	Bukva Balázs, Gáspár Attila, Imolay András, Matolcsi Dávid, Szabó Kristóf.
4 pontot kapott:	Márton Dénes.
0 pontot kapott:	2 versenyző.

A KöMaL 2018. márciusi matematika feladatai