Az A. 855. feladat (2023. május)

A. 855. A nem egyenlőszárú \(\displaystyle ABC\) háromszög legrövidebb oldala \(\displaystyle BC\). Vegyük fel az \(\displaystyle M\) és az \(\displaystyle N\) pontot az \(\displaystyle AB\), illetve az \(\displaystyle AC\) oldalon úgy, hogy \(\displaystyle BM=CN= BC\) teljesüljön. Jelölje \(\displaystyle D\) és \(\displaystyle E\) az \(\displaystyle AMN\) háromszög beírt és körülírt körének középpontját, jelölje továbbá \(\displaystyle I\) és \(\displaystyle O\) az \(\displaystyle ABC\) háromszög beírt és körülírt körének középpontját. Bizonyítsuk be, hogy a \(\displaystyle DE\) és \(\displaystyle IO\) egyenesek az \(\displaystyle ABC\) háromszög körülírt körén metszik egymást.

Javasolta: Luu Dong (Vietnám)

(7 pont)

A beküldési határidő 2023. június 12-én LEJÁRT.

Jelöljük \(\displaystyle (XYZ)\)-vel az \(\displaystyle X\), \(\displaystyle Y\) és \(\displaystyle Z\) nem egy egyenesen fekvő pontok köréírt körét. Legyen \(\displaystyle H\) az \(\displaystyle (AMN)\) és \(\displaystyle (ABC)\) körök második metszéspontja. Ismert, hogy \(\displaystyle H\) éppen a \(\displaystyle BMCN\) négyszö Miquel-pontja, azaz \(\displaystyle H\) annak a forgatvanyújtásnak a középpontja, ami a \(\displaystyle BM\) szakaszt a \(\displaystyle CN\) szakaszba viszi, vagy máshogy mondva, \(\displaystyle HBM\) és \(\displaystyle HCN\) háromszögek hasonlóak. Azonban a feladat feltételei szerint \(\displaystyle BM=CN\), így a két háromszög egybevágó, tehát \(\displaystyle HM=HN\) és \(\displaystyle HB=HC\). Ez éppen azt jelenti, hogy \(\displaystyle H\) az \(\displaystyle (ABC)\) és \(\displaystyle (AMN)\) körökön rendre az \(\displaystyle A\)-t tartalmazó \(\displaystyle BC\) és \(\displaystyle MN\) körívek felezőpontja.

Messe az \(\displaystyle IO\) félegyenes az \(\displaystyle (ABC)\) kört a \(\displaystyle K\) pontban. Legyen \(\displaystyle F\) és \(\displaystyle G\) a \(\displaystyle H\)-val szemközti pont rendre az \(\displaystyle (AMN)\) és \(\displaystyle (ABC)\) körökön, azaz \(\displaystyle F\) és \(\displaystyle G\) az \(\displaystyle A\)-t nem tartalmazó \(\displaystyle MN\) és \(\displaystyle BC\) ív felezőpontja az \(\displaystyle (AMN)\) és \(\displaystyle (ABC)\) körökön. Ekkor az \(\displaystyle A\), \(\displaystyle D\), \(\displaystyle F\), \(\displaystyle I\) és \(\displaystyle G\) pontok egy egyenesre esnek, a \(\displaystyle BAC \sphericalangle\) szögfelezőjére.

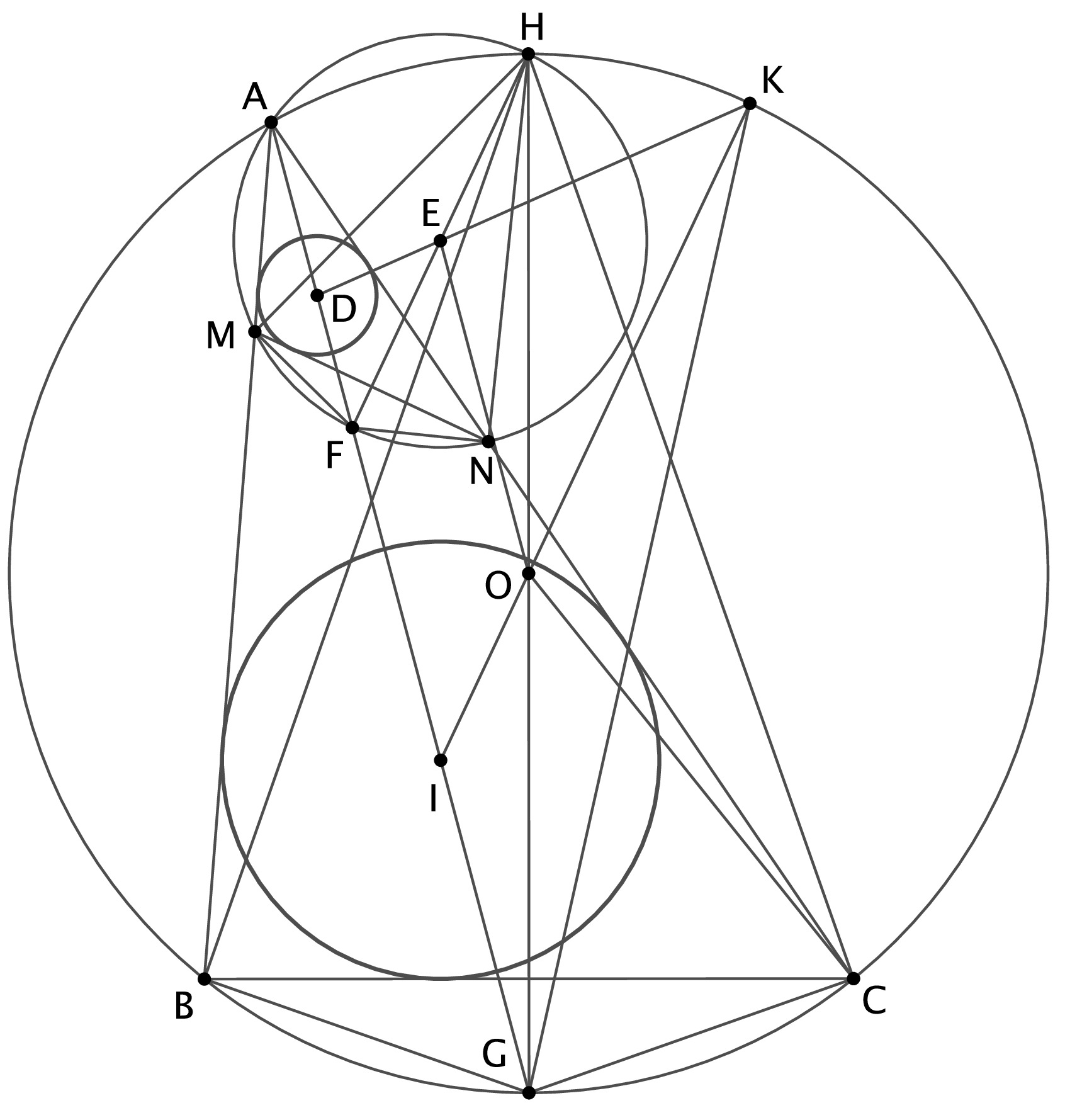
1. Állítás: A \(\displaystyle HBC\), \(\displaystyle OGC\) és \(\displaystyle EFN\) háromszögek hasonlóak.

Bizonyítás: A kerületi és középponti szögek tétetéből világos, hogy \(\displaystyle GOC \sphericalangle=BHC \sphericalangle\), és \(\displaystyle OG=OC\), \(\displaystyle HB=HC\), azaz \(\displaystyle OGC\) és \(\displaystyle HBC\) háromszögek tényleg hasonlóak. Ugyanígy az \(\displaystyle (AMN)\) körben felírt kerületi és középponti szögek tétele miatt \(\displaystyle EFN\) és \(\displaystyle HMN\) háromszögek is hasonlóak. Végül abból, hogy \(\displaystyle H\) a \(\displaystyle BMCN\) négyszög Miquel-pontja az is következik, hogy \(\displaystyle HMN\) és \(\displaystyle HBC\) hasonlóak, ezzel az állítást bizonyítottuk.

Állítás 2: Az \(\displaystyle IO\) és \(\displaystyle EF\) egyenesek párhuzamosak.

Bizonyítás: Fiegyeljük meg, hogy \(\displaystyle H\) a \(\displaystyle GFCN\) négyszögnek is Miquel-pontja, így \(\displaystyle HFG\) és \(\displaystyle HNC\) háromszögek hasonlóak. Ismert, hogy \(\displaystyle GI=GC\), így \(\displaystyle \frac{GI}{GO}=\frac{GC}{GO}=\frac{BC}{HC}=\frac{CN}{HC}\), ahol a második egyenlőségnél az 1. Állítást, a harmadikbál pedig a feladat \(\displaystyle BC=CN\) feltételét használtuk. Emellett \(\displaystyle OGI \sphericalangle=HGA \sphericalangle=HCA \sphericalangle=HCN \sphericalangle\), tehát az \(\displaystyle OGI\) és \(\displaystyle HCN\) háromszögek két oldalának az aránya, és a közrezárt szög megegyezik, azaz hasonlóak. Következésképpen, \(\displaystyle OGI\) a \(\displaystyle HGF\) háromszöggel is hasonló, amiből adódik, hogy \(\displaystyle IO\) és \(\displaystyle FE\) párhuzamosak.

3. Állítás: Az \(\displaystyle EO\) és \(\displaystyle FI\) egyenesek párhuzamosak, valamint \(\displaystyle EO=GC\).

Bizonyítás: Az \(\displaystyle EO\) szakasz középvonal a \(\displaystyle HFG\) háromszögben, amiből azonnal adódik, hogy \(\displaystyle EO\) és \(\displaystyle FI\) párhuzamosak. A 2. Állítást felhasználva \(\displaystyle EFIO\) paralelogramma, így \(\displaystyle EO=FI=GI=GC\), ahol a második egyenlőség azért teljesül, mert \(\displaystyle EO\) középvonal, így \(\displaystyle 2 \cdot EO=FG\), a harmadik pedig megint az ismert \(\displaystyle GI=GC\) egyenlőség.

Ezen állításokkal felfegyverkezve már nem nehéz bizonyítani a feladat állítását. Beláttuk a 2. és 3. Állításban, hogy \(\displaystyle FE\) és \(\displaystyle OK\) valamint \(\displaystyle DF\) és \(\displaystyle EO\) párhuzamosak.

\(\displaystyle \frac{DF}{FE}=\frac{FN}{FE}=\frac{GC}{GO}=\frac{OE}{OK},\)

ahol az első egyenlőség az ismert \(\displaystyle DF=FN\) miatt teljesül, a második egyenlőség az 1. Állításból adódik, a harmadik pedig abból, hogy \(\displaystyle OG\) és \(\displaystyle OK\) sugarak, valamint a 3. Állításból. Tehát \(\displaystyle DFE\) és \(\displaystyle EOK\) háromszögek két oldala párhuzamos, és ezen oldalak aránya megegyezik, így hasonlóak, és a harmadik oldaluk is párhuzamos, azaz \(\displaystyle DE\) és \(\displaystyle EK\) párhuzamos, ami éppen azt jelenti, hogy \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle K\) egy egyenesen vannak, és ezt akartuk bizonyítani.

Statisztika:

8 dolgozat érkezett.
7 pontot kapott:	Bodor Mátyás, Foris Dávid, Sida Li, Varga Boldizsár, Wiener Anna.
6 pontot kapott:	Lovas Márton.
5 pontot kapott:	1 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2023. májusi matematika feladatai