Az A. 897. feladat (2025. január)

A. 897. A derékszögű koordináta-rendszerben jelölje \(\displaystyle O\) az origót és \(\displaystyle \gamma\) az \(\displaystyle (1,0)\) középpontú, egység sugarú kört. Legyen \(\displaystyle \lambda\) egy valós szám a \(\displaystyle (0,2)\) intervallumból, és legyen az \(\displaystyle x=\lambda\) egyenes és a \(\displaystyle \gamma\) kör két metszéspontja \(\displaystyle P\) és \(\displaystyle Q\). Az \(\displaystyle OP\) és \(\displaystyle OQ\) egyenesek az \(\displaystyle x=2-\lambda\) egyenest rendre a \(\displaystyle P'\) és \(\displaystyle Q'\) pontokban metszik. Az ilyen \(\displaystyle P'\), \(\displaystyle Q'\) pontok mértani helyét jelöljük \(\displaystyle \mathcal{G}\)-vel, ahogy \(\displaystyle \lambda\) bejárja a \(\displaystyle (0,2)\) intervallumot. Mutassuk meg, hogy vannak olyan \(\displaystyle O\)-tól különböző \(\displaystyle R\) és \(\displaystyle S\) pontok a síkon, amelyekre minden \(\displaystyle A\in \mathcal{G}\) pontra létezik olyan \(\displaystyle A'\) pont az \(\displaystyle OA\) egyenesen, hogy

\(\displaystyle A'R^2=(A'S-OS)^2=A'A\cdot A'O. \)

Javasolta: Bán-Szabó Áron (Budapest)

Figyelem! A feladat szövegébe apró diszkussziós hiba csúszott. A bizonyítandó állítás végén szereplő egyenlőség helyes alakja: \(\displaystyle A'R^2=(A'S\pm OS)^2=A'A\cdot A'O\).

(7 pont)

A beküldési határidő 2025. február 10-én LEJÁRT.

Először lássuk be, hogy \(\displaystyle \mathcal{G}\)-t invertálva az origó középpontú kettő sugarú körre egy vízszintes parabolát kapunk. Két fajta bizonyítást mutatunk erre, mindkettőben \(\displaystyle P'\) inverzéről látjuk be, hogy egy fix parabolán mozog, hiszen a tengelyes szimmetria miatt ez elégséges.

I. Számolós módszer: Világos, hogy mivel az origó, \(\displaystyle P\) és a \(\displaystyle (2,0)\) pont egy derékszögű háromszög három csúcsa, a magasságtétel szerint \(\displaystyle P=(\lambda,\lambda(2-\lambda)^{1/2})\). Innen \(\displaystyle P'\)-t úgy kapjuk meg, hogy annyira felnagyítjuk \(\displaystyle P\)-t az origóból, hogy az \(\displaystyle x\)-kooridnátája \(\displaystyle 2-\lambda\) legyen, azaz \(\displaystyle P'=(2-\lambda,\frac{(2-\lambda)^{3/2}}{\lambda^{1/2}})\). Az origó középpontú \(\displaystyle 2\) sugarú körre invertálva az \(\displaystyle (x,y)\) pont képe \(\displaystyle (\frac{4x}{x^2+y^2},\frac{4y}{x^2+y^2})\) lesz, tehát \(\displaystyle P'\) inverze \(\displaystyle \left (\dfrac{4(2-\lambda)}{(2-\lambda)^2+\frac{(2-\lambda)^3}{\lambda}},\dfrac{\frac{4(2-\lambda)^{3/2}}{\lambda^{1/2}}}{(2-\lambda)^2+\frac{(2-\lambda)^3}{\lambda}}\right)\). Belátjuk, hogy ez a pont rajta fekszik az \(\displaystyle x=y^2/2\) egyenletű parabolán.

Ezt akartuk igazolni.

II. Projektív, fokozós módszer: (A módszerről Vladyslav Zveryk “The Method of Moving Points" című angol nyelvű cikkében érdemes olvasni.) Jelölje \(\displaystyle X^*\) az \(\displaystyle X\) alakzat (pont, egyenes vagy kör) inverz képét. Jelölje \(\displaystyle V\) azt a metszéspontját az \(\displaystyle x=2-\lambda\) egyenesnek a körrel, ami az \(\displaystyle x\)-tengely ugyanazon oldalán van, mint \(\displaystyle P\). Mivel az \(\displaystyle (1,0)\) középpontú, egységsugarú kör inverze az \(\displaystyle x=2\) egyenes, ezen rajta vannak a \(\displaystyle P^*,V^*\) pontok. Mozogjon \(\displaystyle P^*\) lineárisan ezen az egyenesen. Vegyük észre, hogy az \(\displaystyle (OP^*V^*)\) kört érinti az \(\displaystyle x\) tengely, hiszen visszainvertálva \(\displaystyle PV\) párhuzamos a tengellyel, és az inverzió szögtartó. Ekkor \(\displaystyle V^*\) is elsőfokon mozog, mivel ha \(\displaystyle B=(2,0)\), akkor \(\displaystyle BO^2=BP^*\cdot BV^*\), azaz \(\displaystyle V^*\) a \(\displaystyle P^*\) harmonikus társa a \(\displaystyle (2,2),(2,-2)\) pontokra nézve. Mivel \(\displaystyle P'V\) merőleges az \(\displaystyle x\)-tengelyre, \(\displaystyle P'^*V^*\) párhuzamos az \(\displaystyle x\)-tengellyel, tehát a \(\displaystyle P'^*V^*,OP^*\) egyenesek mind elsőfokúak (egy fix ponton és egy elsőfokú mozgó ponton átmenő egyenesek). Így metszéspontjuk, \(\displaystyle P'^*\) másodfokú (könnyű látni, hogy elsőfokú nem lehet). Világos, hogy \(\displaystyle O\)-t tartalmazza ez a másodfokú görbe, illetve, hogy pontosan egy darab ideális ponton megy át (amikor \(\displaystyle P=B\), avagy \(\displaystyle V=O\)), tehát egy origó csúcsú vízszintes parabola.

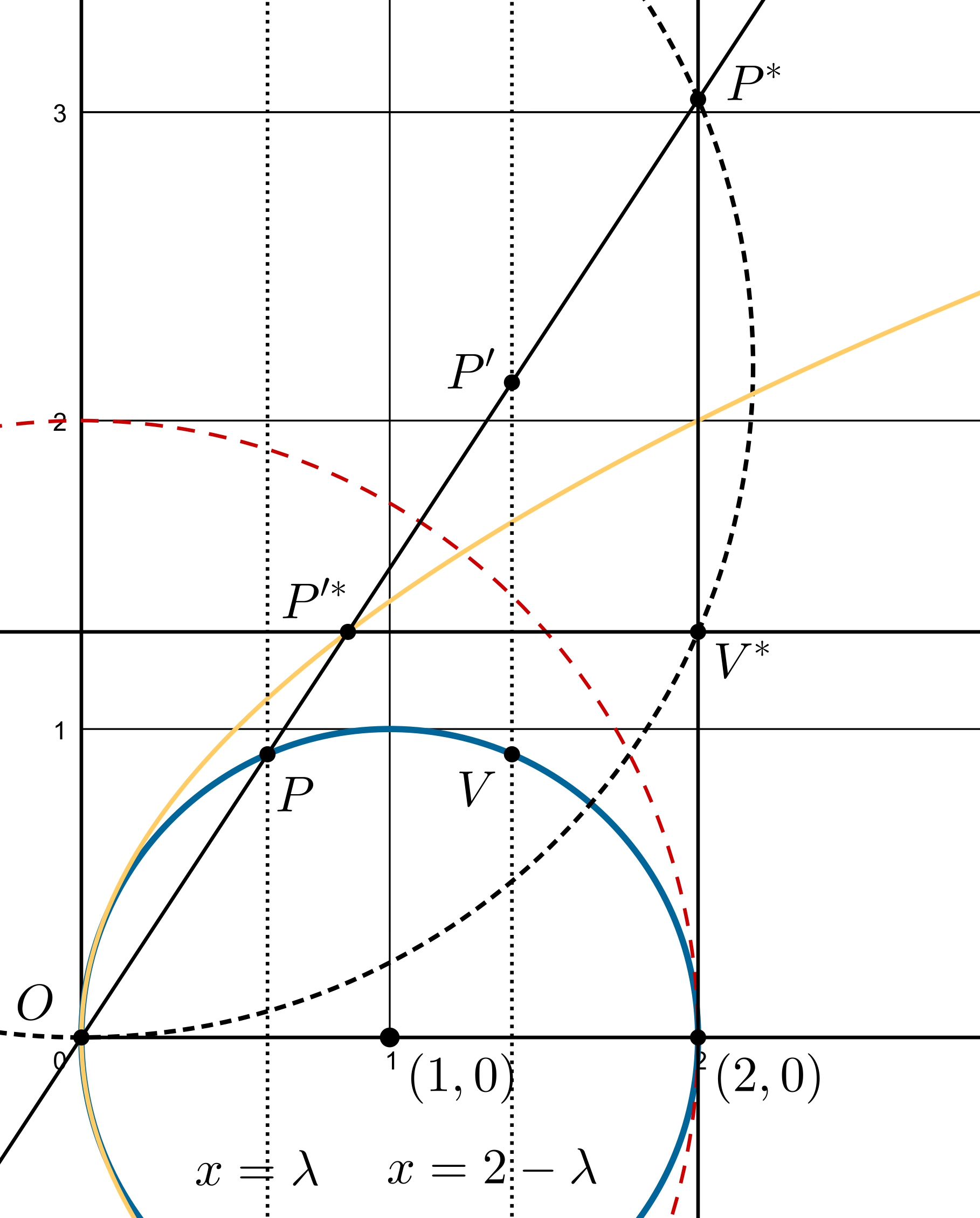
Legyen ennek a parabolának a fókusza \(\displaystyle F\), vezéregyenese \(\displaystyle v\). Ekkor a parabola minden \(\displaystyle A^*\) pontja egyenlő távolságra van \(\displaystyle F\)-től és \(\displaystyle v\)-től. Jelölje \(\displaystyle T\) az \(\displaystyle A^*\)-ból \(\displaystyle v\)-re állított merőleges talppontját. Ekkor \(\displaystyle |A^*F|=|A^*T|\). Legyen \(\displaystyle R\) az \(\displaystyle F\) pont inverze az origó középpontú kettő sugarú körre, míg \(\displaystyle S\) a \(\displaystyle v\) inverzének - ami egy kör - a középpontja. Ha most invertáljuk az \(\displaystyle A^*\) középpontú \(\displaystyle F,T\) pontokon átmenő kört, akkor egy másik kört kapunk, melynek középpontját válasszuk \(\displaystyle A'\)-nek. Ekkor mivel az \(\displaystyle A^*\) középpontú \(\displaystyle T\)-n átmenő kör érinti \(\displaystyle v\)-t, az inverzeik is érintik egymást. Továbbá ezen körre nézve (mármint az \(\displaystyle A^*\) középpontú \(\displaystyle T\)-n átmenő körre nézve) \(\displaystyle A^*\) és a végtelen pont egymás inverzei, így az invertálás után \(\displaystyle O\) és \(\displaystyle A\) egymás inverzei lesznek az inverz körre nézve. Tehát ha a két kör kívülről érinti egymást, akkor

\(\displaystyle AA'\cdot A'O=A'R^2\qquad \text{és} \qquad A'R=A'S-OS,\)

ha pedig a két kör belülről érinti egymást, akkor

\(\displaystyle AA'\cdot A'O=A'R^2\qquad \text{és} \qquad A'R=A'S+OS.\)

Statisztika:

6 dolgozat érkezett.
7 pontot kapott:	Bodor Mátyás, Minh Hoang Tran, Szakács Ábel, Tianyue DAI, Varga Boldizsár.
5 pontot kapott:	1 versenyző.

A KöMaL 2025. januári matematika feladatai