 |
A B. 3806. feladat (2005. március) |
B. 3806. Adott a síkon két egymáson kívül elhelyezkedő kör, és mindegyiküknek egy-egy átmérője, amelyeknek az egyenese érinti a másik kört. Bizonyítsuk be, hogy a két átmérő végpontjai egy trapézt határoznak meg.
(4 pont)
A beküldési határidő 2005. április 15-én LEJÁRT.
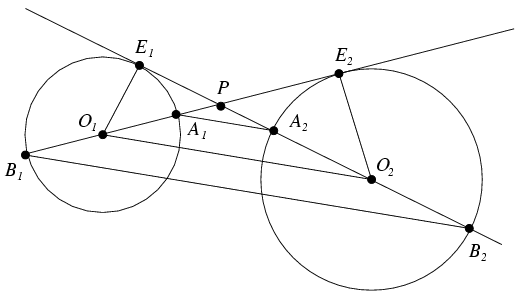
Megoldás. Ha a két érintő véletlenül párhuzamos egymással (egybe nyilván nem eshetnek), akkor az állítás nyilvánvaló. Egyebként jelölje metszéspontjukat P. Az első kör középpontját jelölje O1, az első körön lévő érintési pontot E1, az átmérő végpontjait pedig A1 és B1 úgy, hogy A1 van közelebb a P ponthoz. A második körhöz tartozó megfelelő pontokat jelölje rendre O2, E2, A2 és B2. PE1O1 és PE2O2 hasonló derékszögű háromszögek, ezért PO1:PO2=r1:r2, ahol r1 és r2 a megfelelő körök sugarának hossza. Ekkor
vagyis a párhuzamos szelők tételének megfordítása alapján . Hasonlóképpen
vagyis . Következésképpen
, és minthogy a négy pont nem lehet egy egyenesen, az A1A2B2B1 négyszög valóban trapéz.
Statisztika:
110 dolgozat érkezett. 4 pontot kapott: 58 versenyző. 3 pontot kapott: 33 versenyző. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 8 versenyző.
A KöMaL 2005. márciusi matematika feladatai
