A B. 3844. feladat (2005. október)

B. 3844. Egy derékszögű háromszög befogóinak hossza a és b, átfogója c. A b befogóhoz írt kör (ami kívülről érinti a befogót és a másik két oldal meghosszabbítását) sugara _b. Igazoljuk, hogy b+c=a+2_b.

(3 pont)

A beküldési határidő 2005. november 15-én LEJÁRT.

Az ábra jelöléseivel élve OX=OY=OZ=_a. Az OXCY négyszögnek három szöge is derékszög, ezért az négyzet, vagyis CX=CY=_a. Az egybevágó OXB és OZB derékszögű háromszögekben BZ=BX=a-_a. AY=AZ miatt

2AY=AY+AZ=(b+_a)+(c+a-_a)=a+b+c,

ahonnan 2(b+_a)=a+b+c, vagyis b+2_a=a+c.

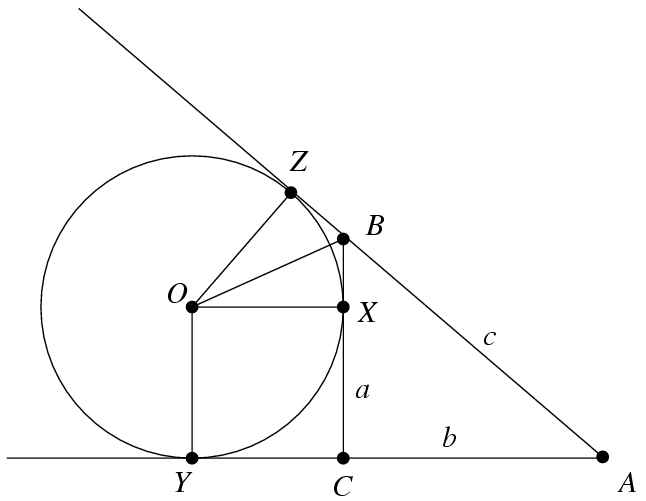
Statisztika:

313 dolgozat érkezett.
3 pontot kapott:	211 versenyző.
2 pontot kapott:	83 versenyző.
1 pontot kapott:	10 versenyző.
0 pontot kapott:	7 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2005. októberi matematika feladatai