 |
A B. 3855. feladat (2005. november) |
B. 3855. Legalább hány hegyesszögű háromszöget kell hézagmentesen és átfedés nélkül összeilleszteni, hogy egy 120o-os szárszögű egyenlő szárú háromszöget kapjunk?
(4 pont)
A beküldési határidő 2005. december 15-én LEJÁRT.
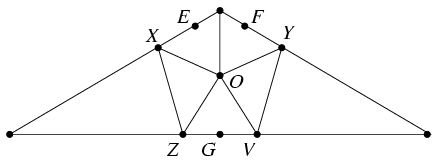
Megoldás: Az alábbi ábra mutatja, hogy hét háromszög elegendő. Itt O a beírt kör középpontja, mely az oldalakat az E,F,G pontokban érinti, az X,Y,Z,V pontokat pedig úgy vettük fel, hogy az OEX,OGZ,OGV,OFY egybevágó derékszögű háromszögek kisebbik hegyesszöge 40o-os.
A továbbiakban megmutatjuk, hogy semmilyen tompaszögű háromszög esetén sem lehet a feladatot hétnél kevesebb hegyesszögű háromszöggel megoldani. Tekintsünk egy tompaszögű háromszöget, amelyet a lehető legkevesebb számú hegyesszögű háromszögből raktunk össze, melyek száma legyen h. Tudjuk már, hogy h 7. A tompaszögű csúcshoz legalább két háromszög illeszkedik. Egy ilyen kis háromszögnek nem lehet másik csúcsa a tompaszöggel szemközti oldal belsejében, mert akkor a kis háromszög egyik oldala az eredeti háromszögből vagy levágna egy tompaszögű háromszöget (aminek felbontásához legalább h hegyesszögű háromszög kellene), vagy pedig azt két derékszögű háromszögre vágná fel, egy derékszögű háromszöget azonban nyilván nem lehet négynél kevesebb hegyesszögű háromszögből összerakni. Van tehát legalább egy belső pont, ami valamelyik kis háromszögnek csúcsa. Egy ilyen belső pont vagy csúcsa legalább 5 kis háromszögnek, nevezzük ezt a) típusúnak, vagy pedig illeszkedik egy kis háromszög oldalára, és csúcsa lagalább 3 további kis háromszögnek, b) típus. Két belső pont egyszerre legfeljebb két háromszög határára eshet, ezért ha több belső pont is szerepel a felbontásban, akkor azonnal adódik, hogy h
7. A tompaszögű csúcshoz legalább két háromszög illeszkedik. Egy ilyen kis háromszögnek nem lehet másik csúcsa a tompaszöggel szemközti oldal belsejében, mert akkor a kis háromszög egyik oldala az eredeti háromszögből vagy levágna egy tompaszögű háromszöget (aminek felbontásához legalább h hegyesszögű háromszög kellene), vagy pedig azt két derékszögű háromszögre vágná fel, egy derékszögű háromszöget azonban nyilván nem lehet négynél kevesebb hegyesszögű háromszögből összerakni. Van tehát legalább egy belső pont, ami valamelyik kis háromszögnek csúcsa. Egy ilyen belső pont vagy csúcsa legalább 5 kis háromszögnek, nevezzük ezt a) típusúnak, vagy pedig illeszkedik egy kis háromszög oldalára, és csúcsa lagalább 3 további kis háromszögnek, b) típus. Két belső pont egyszerre legfeljebb két háromszög határára eshet, ezért ha több belső pont is szerepel a felbontásban, akkor azonnal adódik, hogy h 7, kivéve ha csak két belső pont van, és mind a kettő b) típusú. Az azonban nem lehet, hogy csak hat háromszög szerepel a felbontásban, melyek mindgyikének valamelyik csúcsa e két b) típusú pont valamelyike. Ha tehát h
7, kivéve ha csak két belső pont van, és mind a kettő b) típusú. Az azonban nem lehet, hogy csak hat háromszög szerepel a felbontásban, melyek mindgyikének valamelyik csúcsa e két b) típusú pont valamelyike. Ha tehát h 6, akkor a felbontásban pontosan egy belső pont szerepel. Ekkor a tompaszögű csúcshoz pontosan két kis háromszög illeszkedik, melyek közül legalább egyiknek csúcsa a szóban forgó belső pont. Ha ez b) típusú lenne, ellentmondásra jutnánk. Abból kiindulva, hogy ez az egyetlen belső pont a) típusú, már nem nehéz igazolni, hogy a felbontásban legalább hét kis háromszög szerepel.
6, akkor a felbontásban pontosan egy belső pont szerepel. Ekkor a tompaszögű csúcshoz pontosan két kis háromszög illeszkedik, melyek közül legalább egyiknek csúcsa a szóban forgó belső pont. Ha ez b) típusú lenne, ellentmondásra jutnánk. Abból kiindulva, hogy ez az egyetlen belső pont a) típusú, már nem nehéz igazolni, hogy a felbontásban legalább hét kis háromszög szerepel.
Statisztika:
123 dolgozat érkezett. 4 pontot kapott: Károlyi Gergely, Kriván Bálint, Nagy 235 János, Tossenberger Anna. 3 pontot kapott: Balambér Dávid, Blázsik Zoltán, Cseh Ágnes, Csima Géza, Csorba János, Duba Zsombor, Fekete Balázs Samu, Herber Máté, Hülber Tímea, Imre Gábor, Kovács 129 Péter, Kristóf Panna, Lamm Éva, Németh 007 Zsolt, Pásztor Attila, Salát Zsófia, Sümegi Károly, Szabó Beáta Tünde, Szakács Nóra, Szécsényi Ágnes, Szirmai Péter, Szudi László, Tolner Ferenc, Tóth 796 Balázs, Tóthmérész Lilla, Wolosz János. 2 pontot kapott: 38 versenyző. 1 pontot kapott: 27 versenyző. 0 pontot kapott: 28 versenyző.
A KöMaL 2005. novemberi matematika feladatai
