A B. 3879. feladat (2006. január)

B. 3879. Egy konvex sokszög hozzáírt körének egy olyan kört nevezünk, amely kívülről érinti a sokszög egyik oldalát és az ezzel szomszédos két oldalnak a meghosszabbítását. A hozzáírt körök kerületének összegét jelölje k, a sokszög oldalai mint átmérők fölé emelt körök területének összegét pedig t.

Tegyük fel, hogy a sokszögbe kör írható, és legyen a kerülete K, a területe pedig T. Mutassuk meg, hogy

$\frac{k}{t}\le \frac{K}{T}.$

(4 pont)

A beküldési határidő 2006. február 15-én LEJÁRT.

Megoldás: Legyenek a sokszög oldalai $a_1,a_2,\ldots, a_n$ , az ezeket érintő hozzáírt körök sugarai rendre $r_1,r_2,\ldots,r_n,$ a beírt kör sugara R. Ekkor $k=\sum_{i=1}^n 2r_i\pi$ , $t=\sum_{i=1}^n(a/2)^2\pi$ , K=2R $\pi$ és T=R² $\pi$ . Ezek alapján a bizonyítandó állítást

$\sum_{i=1}^n 4Rr_i\le \sum_{i=1}^n a_i^2$

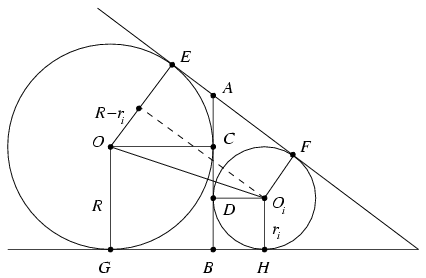
alakba írhatjuk át. Megmutatjuk, hogy minden i-re 4Rr_i $\le$ a_i². Legyen az i-edik oldal két végpontja A és B, ezt a beírt kör és a hozzáírt kör a C,D pontokban érinti. Ugyanezek a körök a szomszédos oldalak egyenesét érintsék az E,F, illetve G,H pontokban az ábra szerint. Ekkor AE=AC, AF=AD, BG=BC és BH=BD miatt

EF+GH=AC+AD+BC+BD=2a_i.

A szimmetria miatt tehát EF=GH=a_i. Ha a két kör középpontját O és O_i jelöli, akkor R+r_i $\le$ OO_i, és itt egyenlőség pontosan akkor áll fenn, ha a C,D pontok az OO_i szakaszra esnek, vagyis ha a sokszög A és B csúcsánál lévő két szöge egyenlő. A Pithagorasz-tétel alapján tehát

R²+2Rr_i+r_i² $\le$ OO_i²=EF²+(R-r_i)²=a_i²+R²-2Rr_i+r_i²,

vagyis valóban 4Rr_i $\le$ a_i². Ezeket az egyenlőtlenséget összegezve kapjuk a bizonyítandó állítást. Az is látszik ebből, hogy egyenlőség pontosan akkor áll fenn, ha a sokszög valamennyi szöge egyenlő. Mivel a sokszögbe kör írható, ez azt jelenti, hogy a sokszög szabályos.

Statisztika:

29 dolgozat érkezett.

4 pontot kapott: Herber Máté, Honner Balázs, Kovács 111 Péter, Kovács 129 Péter, Páldy Sándor, Sümegi Károly, Szalóki Dávid, Szirmai Péter, Szűcs Gergely, Tomon István.

3 pontot kapott: Blázsik Zoltán, Bogár 560 Péter, Csaba Ákos, Cseh Ágnes, Godó Zita, Horváth 385 Vanda, Komáromy Dani, Kunovszki Péter, Kurgyis Eszter, Nagy 235 János, Peregi Tamás, Sóti Gergely, Szakács Nóra, Szilágyi 987 Csaba, Tossenberger Anna, Udvari Balázs.

2 pontot kapott: 1 versenyző.

1 pontot kapott: 1 versenyző.

0 pontot kapott: 1 versenyző.

A KöMaL 2006. januári matematika feladatai

29 dolgozat érkezett.
4 pontot kapott:	Herber Máté, Honner Balázs, Kovács 111 Péter, Kovács 129 Péter, Páldy Sándor, Sümegi Károly, Szalóki Dávid, Szirmai Péter, Szűcs Gergely, Tomon István.
3 pontot kapott:	Blázsik Zoltán, Bogár 560 Péter, Csaba Ákos, Cseh Ágnes, Godó Zita, Horváth 385 Vanda, Komáromy Dani, Kunovszki Péter, Kurgyis Eszter, Nagy 235 János, Peregi Tamás, Sóti Gergely, Szakács Nóra, Szilágyi 987 Csaba, Tossenberger Anna, Udvari Balázs.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

Már regisztráltál?
Új vendég vagy?