A B. 3919. feladat (2006. május)

B. 3919. Szerkesszünk a hegyesszögű ABC háromszög belsejében olyan P pontot, amelyre PA^.BC=PB^.CA=PC^.AB.

Javasolta: Holló Gábor (Budapest)

(3 pont)

A beküldési határidő 2006. június 15-én LEJÁRT.

Megoldás: Az első feltétel azzal ekvivalens, hogy PA:PB=CA:CB, vagyis hogy P arra a k_c Apollóniusz-körre illeszkedik, amelynek középpontja az AB egyenesen van, és amely áthalad mind a C csúcson, mind pedig (a szögfelező-tétel értelmében) a C-ből induló szögfelezőnek az AB oldallal alkotott F_c metszéspontján. (A CA=CB esetben k_c az AB oldal felező merőlegesévé fajul el.) A második feltétel pedig azzal ekvivalens, hogy P illeszkedik arra a k_a Apollóniusz-körre, amelynek középpontja a BC egyenesen van, és amely áthalad mind az A csúcson, mind pedig az A-ból induló szögfelezőnek a BC oldallal alkotott F_a metszéspontján. E két evidens módon megszerkeszthető körnek a háromszögbe eső metszéspontja szolgáltatja a P pontot.

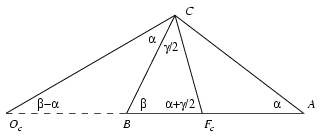
Hogy pontosan egy ilyen P pont létezik, ahhoz elég annyit látni, hogy a k_c (illetve k_a) körnek a C-t F_c-vel (A-t F_a-val) összekötő rövidebb íve végig a háromszög belsejében halad. Ez az elfajuló esetben triviálisan teljesül, ha pedig például $\beta$ > $\alpha$ , akkor az első állítás abból következik, hogy az O_cCA szög derékszögnél nagyobb, ahol O_c a k_c középpontja. Ezt pedig egyszerű szögszámolással így igazolhatjuk: mivel a BCF_c háromszögben a BCF_c szög $\gamma$ /2, a BF_cC szög $\alpha$ + $\gamma$ /2 lesz, ezért az O_cF_cC egyenlő szárú háromszög miatt az O_cCB szög $\alpha$ , és végül az O_cCA szög $\alpha$ + $\gamma$ , ami nagyobb 90^o-nál, mivel az ABC háromszög hegyesszögű.

Statisztika:

33 dolgozat érkezett.

3 pontot kapott: Bartha Zsolt, Faragó Kornél, Farkas Márton, Grósz Dániel, Győrffy Lajos, Herber Máté, Nagy 235 János, Sommer Dániel, Szabó Levente, Szakács Nóra, Szalkai Balázs, Szívós Eszter, Ta Phuong Linh, Tallián György, Tóth 222 Barnabás, Tóthmérész Lilla, Varga 111 Péter.

2 pontot kapott: Csató László, Földes Imre, Godó Zita, Károlyi Gergely, Milotai Zoltán, Nagy 314 Dániel, Nagy-Baló András, Páldy Sándor, Tóth 796 Balázs, Véges Márton.

1 pontot kapott: 1 versenyző.

0 pontot kapott: 5 versenyző.

A KöMaL 2006. májusi matematika feladatai

33 dolgozat érkezett.
3 pontot kapott:	Bartha Zsolt, Faragó Kornél, Farkas Márton, Grósz Dániel, Győrffy Lajos, Herber Máté, Nagy 235 János, Sommer Dániel, Szabó Levente, Szakács Nóra, Szalkai Balázs, Szívós Eszter, Ta Phuong Linh, Tallián György, Tóth 222 Barnabás, Tóthmérész Lilla, Varga 111 Péter.
2 pontot kapott:	Csató László, Földes Imre, Godó Zita, Károlyi Gergely, Milotai Zoltán, Nagy 314 Dániel, Nagy-Baló András, Páldy Sándor, Tóth 796 Balázs, Véges Márton.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	5 versenyző.

Már regisztráltál?
Új vendég vagy?