 |
A B. 4018. feladat (2007. szeptember) |
B. 4018. Az AB átmérőjű kör B-beli érintőjén adott egy P pont. A P-ből a körhöz húzott másik érintő érintési pontja C. A C pont merőleges vetülete az AB egyenesen T. Bizonyítsuk be, hogy AP felezi a CT szakaszt.
(4 pont)
A beküldési határidő 2007. október 15-én LEJÁRT.
Megoldás: Legyen a kör középpontja O, a C pontnak a BP egyenesre eső vetülete S, az AP és CT szakaszok metszéspontja pedig legyen Q. Az egyszerűség kedvéért vegyünk fel egy derékszögű koordinátarendszert, melynek középpontja O, a B pont koordinátái B(1;0), a P(1;p) pont második koordinátája pedig pozitív. A többi pont koordinátái ekkor A(-1;0), T(t;0), Q(t;q), C(t;c) és S(1;c) lesznek alkalmas t,q,c számokkal. Azt kell belátnunk, hogy q=c/2. Itt q,c>0, t pedig attól függően lesz pozitív, nagatív, vagy 0, hogy p értéke 0 és 1 közé esik, 1-nél nagyobb, vagy pedig 1-gyel egyenlő. A kör egyenlete x2+y2=1, tehát t2+c2=1.
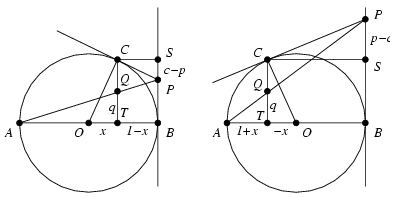
A CTO (t=0 esetén elfajuló) derékszögű háromszöget mindhárom esetben C körüli 90o-os forgatva nyújtás viszi a CSP háromszögbe, a megfelelő oldalak arányára tehát t:c=(c-p):(1-t) írható fel, ahonnan t-t2=c2-cp, cp=t2+c2-t=1-t adódik. Az ATC és ABP derékszögű háromszögek hasonlóságából pedig a q:(1+t)=p:2 arányosságot kapjuk, ahonnan
amint azt bizonyítanunk kellett.
Statisztika:
114 dolgozat érkezett. 4 pontot kapott: 71 versenyző. 3 pontot kapott: 18 versenyző. 2 pontot kapott: 11 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 9 versenyző.
A KöMaL 2007. szeptemberi matematika feladatai
