A B. 4110. feladat (2008. szeptember)

B. 4110. Az ABCDEF hatszög és a PQR háromszög úgy helyezkedik el a síkon, hogy az ABRQ, CDPR, EFQP négyszögek téglalapok.

a) Bizonyítsuk be, hogy a BC, DE, FA oldalak felezőmerőlegesei egy ponton mennek át.

b) Mutassuk meg, hogy létezik olyan P'Q'R' háromszög is, amelyre a BCR'Q', DEP'R', FAQ'P' négyszögek téglalapok.

(5 pont)

A beküldési határidő 2008. október 15-én LEJÁRT.

Megoldás: Tegyük fel, hogy a (2) állítást már igazoltuk. Ekkor a BC, DE, FA oldalak felezőmerőlegesei megegyeznek az R'Q', P'R', Q'P' szakaszok felezőmerőlegeseivel, melyek nyilván a P'Q'R' háromszög köré írható kör középpontjában metszik egymást, igazolva az (1) állítást. A (2) állítás igazolásához először a következő önmagában is érdekes segédtételt bizonyítjuk.

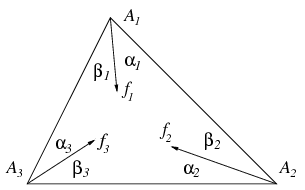
Az A₁A₂A₃ háromszög A_i csúcsából a háromszög belsejében induló f_i félegyenes zárjon be a háromszög megfelelő oldalaival $\alpha$ _i, illetve $\beta$ _i szöget az ábrán látható módon. Az f₁,f₂,f₃ félegyenesek pontosan akkor mennek át egy ponton, ha

sin $\alpha$ ₁sin $\alpha$ ₂sin $\alpha$ ₃=sin $\beta$ ₁sin $\beta$ ₂sin $\beta$ ₃.

Valóban, ha a félegyenesek a P pontban metszik egymást, mely nyilván a háromszög belsejében fekszik, akkor a szinusz-tétel alapján

$\frac{\sin\alpha_1}{\sin\beta_2}\cdot\frac{\sin\alpha_2}{\sin\beta_3}\cdot \frac{\sin\alpha_3}{\sin\beta_1}=\frac{PA_2}{PA_1}\cdot \frac{PA_3}{PA_2}\cdot\frac{PA_1}{PA_3}=1.$

Megfordítva, tegyük fel, hogy sin $\alpha$ ₁sin $\alpha$ ₂sin $\alpha$ ₃=sin $\beta$ ₁sin $\beta$ ₂sin $\beta$ ₃, és a háromszögnek az A₁ csúcsnál lévő szöge hegyesszög. Jelölje P az f₂ és f₃ félegyenesek metszéspontját, mely nyilván a háromszög belsejébe esik, az A₁P félegyenesnek a megfelelő oldalakkal bezárt szögét pedig $\alpha$ ₁', illetve $\beta$ ₁'. A feltételt egybevetve a segédtétel már igazolt felével kapjuk, hogy sin $\alpha$ ₁'/sin $\beta$ ₁'=sin $\alpha$ ₁/sin $\beta$ ₁. Mivel 0<x< $\alpha$ <90^o esetén az f(x)=sin x/sin ( $\alpha$ -x) függvény szigorúan monoton nő, ebből $\alpha$ ₁'= $\alpha$ ₁ adódik, ami azt jelenti, hogy az f₁ félegyenes is áthalad a P ponton.

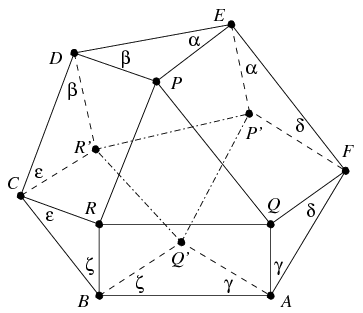
A fenti segédtétel felhasználásával a (2) állítás már könnyen levezethető. Párhuzamos eltolással vigyük a BRC, illetve AQF háromszögeket olyan helyzetbe, hogy a C pont D-be, az F pont pedig E-be kerüljön. Ekkor az R és a Q pont is P-be kerül, minek folytán a B és A pontok ugyanazon G pontba kerülnek. A DEG háromszögre alkalmazva a segédtételt kapjuk, hogy sin $\alpha$ sin $\gamma$ sin $\varepsilon$ =sin $\beta$ sin $\delta$ sin $\zeta$ . Most alkalmazzunk párhuzamos eltolásokat az AB, CD, illetve EF szakaszokra olyan módon, hogy D és E ugyanazon X, F és A ugyanozon Y, B és C pedig ugyanazon Z pontba kerüljenek. Az XYZ háromszögben vegyük fel az X-ből kiinduló f, az Y-ból kiinduló g és a Z-ből kiinduló h félegyeneseket úgy, hogy f az XY oldallal $\alpha$ , g az YZ oldallal $\gamma$ , h pedig a ZX oldallal $\varepsilon$ szöget zárjon be, ekkor f az XZ oldallal $\beta$ , g az YX oldallal $\delta$ , h pedig a ZY oldallal $\zeta$ szöget zár be. Ekkor a segédtétel másik irányát használva azt kapjuk, hogy az f,g,h félegyenesek egy közös U pontban metszik egymást. Az U pontra az iménti eltolások inverzét alkalmazva éppen a megfelelő Q', R', illetve P' ponthoz jutunk.

Statisztika:

18 dolgozat érkezett.

5 pontot kapott: Bálint Dániel, Bodor Bertalan, Éles András, Fonyó Dávid, Huszár Kristóf, Kalina Kende, Lovas Lia Izabella, Nagy 648 Donát.

3 pontot kapott: 2 versenyző.

2 pontot kapott: 1 versenyző.

1 pontot kapott: 4 versenyző.

0 pontot kapott: 3 versenyző.

A KöMaL 2008. szeptemberi matematika feladatai

18 dolgozat érkezett.
5 pontot kapott:	Bálint Dániel, Bodor Bertalan, Éles András, Fonyó Dávid, Huszár Kristóf, Kalina Kende, Lovas Lia Izabella, Nagy 648 Donát.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	3 versenyző.

Már regisztráltál?
Új vendég vagy?