A B. 4184. feladat (2009. május)

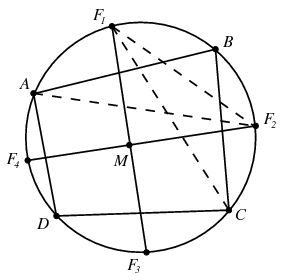
B. 4184. Egy húrnégyszög csúcsai a körülírt kört négy ívre osztják, melyek felezőpontjai sorban F₁, F₂, F₃ és F₄. Mutassuk meg, hogy az F₁F₃ szakasz merőleges F₂F₄-re.

(3 pont)

A beküldési határidő 2009. június 15-én LEJÁRT.

Megoldás. A sokszög csúcsai legyenek A,B,C,D az ábrán látható módon, az átlók metszéspontja legyen M. Az egymástól páronként diszjunkt AB,BC,CD,DA ívekhez tartozó középponti szögeket jelölje rendre $\alpha$ , $\beta$ , $\gamma$ , $\delta$ , ezek összege nyilván 2 $\pi$ .

Az F₂ pontból az AB ív $\alpha$ /2 szög alatt látszik, ezért az AF₁ ív $\alpha$ /4 szög alatt látszik. Az AF₂F₄ szög nagysága hasonlóképpen $\delta$ /4, vagyis az F₁F₂F₄ szög nagysága ( $\alpha$ + $\delta$ )/4. Ugyanígy számolhatjuk ki azt is, hogy az F₂F₁F₃ szög nagysága ( $\beta$ + $\gamma$ )/4. Ezek alapján az F₁F₂M háromszögben az F₁ és F₂ csúcsoknál lévő szögek összege ( $\alpha$ + $\beta$ + $\gamma$ + $\delta$ )/4= $\pi$ /2, tehát az M csúcsnál lévő szög valóban derékszög.

Statisztika:

75 dolgozat érkezett.

3 pontot kapott: 53 versenyző.

2 pontot kapott: 15 versenyző.

1 pontot kapott: 2 versenyző.

0 pontot kapott: 1 versenyző.

Nem versenyszerű: 4 dolgozat.

A KöMaL 2009. májusi matematika feladatai

75 dolgozat érkezett.
3 pontot kapott:	53 versenyző.
2 pontot kapott:	15 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	4 dolgozat.

Már regisztráltál?
Új vendég vagy?