Problem B. 4250. (February 2010)

B. 4250. The centre of the regular hexagon ABCDEF in the coordinate plane is at the origin O, and vertex A is the point (0,1). Let $\mathcal{H}_1$ and $\mathcal{H}_2$ denote the set of points inside or on the boundary of the regular triangles ACE and BDF, respectively. Determine the set of points P for which the vector $\overrightarrow{OP}$ can be written in the form $\overrightarrow{OP_1}+\overrightarrow{OP_2}$ , where $P_1\in \mathcal{H}_1$ and $P_2\in \mathcal{H}_2$ .

(4 pont)

Deadline expired on March 10, 2010.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A $\displaystyle BF$ szakaszt az $\displaystyle \overrightarrow{OA}$ vektorral eltolva az $\displaystyle XY$ szakaszt kapjuk, ahol $\displaystyle X(\sqrt{3}/2;3/2)$ és $\displaystyle Y(-\sqrt{3}/2;3/2)$. Az $\displaystyle XY$ szakasz pontjai tehát a keresett $\displaystyle \mathcal{H}$ halmazhoz tartoznak. Szimmetria okok miatt az $\displaystyle O$ középpontú $\displaystyle XYZUVW$ szabályos hatszög kerületének minden pontja $\displaystyle \mathcal{H}$-hoz tartozik.

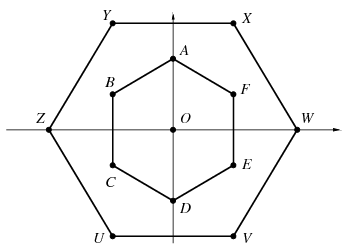
A $\displaystyle \mathcal{H}$ halmaz nyilván konvex, hiszen ha $\displaystyle P,Q\in\mathcal{H}$, vagyis alkalmas $\displaystyle P_i,Q_i\in\mathcal{H}_i$ pontokkal $\displaystyle \overrightarrow{OP}= \overrightarrow{OP_1}+\overrightarrow{OP_2}$ és $\displaystyle \overrightarrow{OQ}= \overrightarrow{OQ_1}+\overrightarrow{OQ_2}$, akkor minden $\displaystyle 0\le \lambda\le 1$ szám esetén a $\displaystyle \mathcal{H}_i$ halmazok konvex volta miatt

$\displaystyle \lambda\overrightarrow{OP}+(1-\lambda)\overrightarrow{OQ}= \left(\lambda\overrightarrow{OP_1}+(1-\lambda)\overrightarrow{OQ_1}\right)+ \left(\lambda\overrightarrow{OP_2}+(1-\lambda)\overrightarrow{OQ_2}\right) \in \mathcal{H}.$

Ezért a keresett $\displaystyle \mathcal{H}$ halmaz az $\displaystyle XYZUVW$ hatszöglemez minden pontját tartalmazza.

Másrészről $\displaystyle \mathcal{H}_1$, illetve $\displaystyle \mathcal{H}_2$ minden pontjának második koordinátája legfeljebb 1, illetve 1/2, vagyis $\displaystyle \mathcal{H}$ egyetlen pontja sem eshet az $\displaystyle XY$ egyenes fölé. Ugyanígy elmondható, hogy $\displaystyle \mathcal{H}$ minden pontja az $\displaystyle XYZUVW$ hatszög bármely oldalegyenesének az origót tartalmazó oldalára esik, vagyis a keresett $\displaystyle P$ pontok halmaza megegyezik az $\displaystyle XYZUVW$ szabályos hatszöglemezzel.

Statistics:

57 students sent a solution.

4 points: Ágoston Tamás, Árvay Balázs, Barczel Nikolett, Beke Lilla, Böőr Katalin, Bősze Zsuzsanna, Csere Kálmán, Éles András, Énekes Péter, Janzer Olivér, Karkus Zsuzsa, Köpenczei Gergő, Lajos Mátyás, Máthé László, Mészáros András, Mihálka Éva Zsuzsanna, Nagy 111 Miklós, Nagy Balázs, Nagy Róbert, Nguyen Milán, Ódor Gergely, Rábai Domonkos, Sándor Áron Endre, Sieben Bertilla, Strenner Péter, Szabó 928 Attila, Varga Vajk, Varju 105 Tamás, Veitz Kristóf Tamás, Weimann Richárd, Weisz Ágoston, Weisz Gellért, Zahemszky Péter, Zsakó András.

3 points: Bauer Barbara, Győrfi 946 Mónika, Hosszejni Darjus, Keresztfalvi Tibor, Remete László, Szenczi Zoltán, Tóth 222 Barnabás.

2 points: 7 students.

1 point: 6 students.

0 point: 3 students.

Problems in Mathematics of KöMaL, February 2010

57 students sent a solution.
4 points:	Ágoston Tamás, Árvay Balázs, Barczel Nikolett, Beke Lilla, Böőr Katalin, Bősze Zsuzsanna, Csere Kálmán, Éles András, Énekes Péter, Janzer Olivér, Karkus Zsuzsa, Köpenczei Gergő, Lajos Mátyás, Máthé László, Mészáros András, Mihálka Éva Zsuzsanna, Nagy 111 Miklós, Nagy Balázs, Nagy Róbert, Nguyen Milán, Ódor Gergely, Rábai Domonkos, Sándor Áron Endre, Sieben Bertilla, Strenner Péter, Szabó 928 Attila, Varga Vajk, Varju 105 Tamás, Veitz Kristóf Tamás, Weimann Richárd, Weisz Ágoston, Weisz Gellért, Zahemszky Péter, Zsakó András.
3 points:	Bauer Barbara, Győrfi 946 Mónika, Hosszejni Darjus, Keresztfalvi Tibor, Remete László, Szenczi Zoltán, Tóth 222 Barnabás.
2 points:	7 students.
1 point:	6 students.
0 point:	3 students.

Already signed up?
New to KöMaL?