 |
A B. 4252. feladat (2010. március) |
B. 4252. Milyen n>2 egészekre igaz a következő állítás? ,,Bármely konvex n-szögnek van olyan oldala, amelyen lévő két szög egyike sem hegyesszög.''
(3 pont)
A beküldési határidő 2010. április 12-én LEJÁRT.
Megoldás. Egy konvex sokszög külső szögeinek összege éppen \(\displaystyle 360^\circ\), ezek közül tehát legfeljebb 3 darab lehet tompaszög. Ezért \(\displaystyle n\ge 7\) esetén kell legyen két szomszédos csúcs, melyek egyikénél lévő külső szög sem tompaszög, vagyis található olyan oldal, amelyen lévő két szög egyike sem hegyesszög. Ha tehát \(\displaystyle n\ge 7\), akkor igaz az állítás.
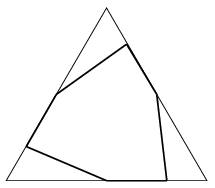
Ha \(\displaystyle n=6\), akkor nem igaz az állítás, ugyanis az ábrán látható konvex hatszög minden második szöge hegyesszög. Ez a hatszög úgy jött létre, hogy egy szabályos háromszög sarkait levágtuk egy-egy olyan szakasszal, amely egy oldalfelező pontot köt össze a levágott csúcshoz illeszkedő másik oldalnak a csúcshoz legközelebbi ötödölőpontjával. (Itt csak arra kellett vigyáznunk, hogy a negyedelőpontnál közelebbi pontot válasszunk, mivel a negyedelőpont esetében kaptunk volna éppen derékszöget.) Ha a levágott sarkokat egyenként visszahelyezzük, akkor meggyőződhetünk arról is, hogy az állítás \(\displaystyle n=5\), \(\displaystyle n=4\) és \(\displaystyle n=3\) esetén sem igaz. Ezzel minden esetet megvizsgáltunk.
Statisztika:
91 dolgozat érkezett. 3 pontot kapott: Ágoston Péter, Bálint Csaba, Barczel Nikolett, Bogár Blanka, Csizmadia Luca, Csuka Róbert, Éles András, Gyarmati Máté, Halász 423 Dániel, Havasi 0 Márton, Hosszejni Darjus, Janzer Olivér, Karkus Zsuzsa, Karl Erik Holter, Keresztfalvi Tibor, Kiss 232 Dóra, Kiss 902 Melinda Flóra, Korondi Zénó, Lajos Mátyás, Máthé László, Medek Ákos, Mihálka Éva Zsuzsanna, Mihálykó András, Nagy Róbert, Nguyen Noémi, Ódor Gergely, Repka 666 Dániel, Sándor Áron Endre, Sieben Bertilla, Szabó 928 Attila, Szórádi Márk, Uray Marcell János, Varga Vajk, Zahemszky Péter, Zelena Réka, Zsiros Ádám. 2 pontot kapott: 27 versenyző. 1 pontot kapott: 14 versenyző. 0 pontot kapott: 11 versenyző. Nem versenyszerű: 3 dolgozat.
A KöMaL 2010. márciusi matematika feladatai
