A B. 4348. feladat (2011. március)

B. 4348. Az ABCD húrnégyszög átlói nem merőlegesek egymásra. Az A, B, C, D csúcsokból a csúcsokon át nem menő átlókra bocsátott merőlegesek talppontjai rendre A', B', C', D'. Az AA' és DD', DD' és CC', CC' és BB', végül a BB' és AA' egyenesek metszéspontjai rendre E, F, G, H. Bizonyítsuk be, hogy az A'B'C'D' olyan húrnégyszög, mely körülírt körének középpontja az EG és FH szakaszok metszéspontja.

Javasolta: Bíró Bálint (Eger)

(5 pont)

A beküldési határidő 2011. április 11-én LEJÁRT.

Megoldás. Ha az átlók metszéspontja \(\displaystyle M\), akkor az általánosság megszorítása nélkül feltehetjük, hogy az \(\displaystyle AMB\) szög hegyesszög. Ebben az esetben az \(\displaystyle A',B', C',D'\) pontok rendre az \(\displaystyle MB, MA, MD, MC\) nyílt félegyeneseken helyezkednek el. Az egyszerűség kedvéért feltesszük, hogy az említett pontok az \(\displaystyle MB, MA, MD, MC\) belsejébe esnek; a feladat állítása a többi esetben is hasonló meggondolásokkal igazolható.

Mivel \(\displaystyle AA'B\angle=AB'B\angle=90^\circ\), az \(\displaystyle ABA'B'\) négyszög húrnégyszög. Ezért \(\displaystyle A'B'D'\angle=ABA'\angle=ABD\angle\). Hasonlóképp \(\displaystyle BB'C'C\) is húrnégyszög, így \(\displaystyle C'B'D'\angle=C'B'C\angle=C'BC\angle=CBD\angle\). Ezek alapján

\(\displaystyle A'B'C'\angle=A'B'D'\angle+C'B'D'\angle=ABD\angle+CBD\angle=ABC\angle.\)

Ugyanígy kapjuk, hogy \(\displaystyle \{A,B,C,D\}\) halmaz tetszőleges 3-elemű \(\displaystyle \{X,Y,Z\}\) részhalmazára \(\displaystyle X'Y'Z'\angle=XYZ\angle\). Kihasználva, hogy \(\displaystyle ABCD\) húrnégyszög,

\(\displaystyle A'B'C'\angle+A'D'C'\angle=ABC\angle+ADC\angle=180^\circ,\)

ami mutatja, hogy az \(\displaystyle A'B'C'D'\) négyszög is húrnégyszög.

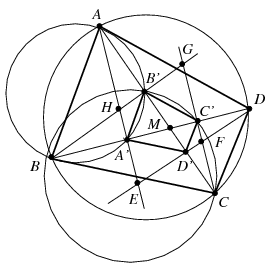
Az \(\displaystyle AA'=EH\) és \(\displaystyle CC'=FG\) egyenesek merőlegesek e négyszög köré írható kör \(\displaystyle A'C'\) húrjára, amiből következik, hogy ugyanolyan távolságra esnek a kör \(\displaystyle O\) középpontjától. Más szóval, az \(\displaystyle EH\) egyenest az \(\displaystyle O\) pontra tükrözve az \(\displaystyle FG\) egyenest kapjuk. Ugyanilyen alapon az \(\displaystyle EF\) egyenes \(\displaystyle O\)-ra vett tükörképe a \(\displaystyle GH\) egyenes lesz. Ez azt jelenti, hogy \(\displaystyle EFGH\) olyan paralelogramma, melynek középpontja, ami egyben az \(\displaystyle EG\) és \(\displaystyle FH\) átlók metszéspontja, egybeesik az \(\displaystyle A'B'C'D'\) húrnégyszög köré írható kör \(\displaystyle O\) középpontjával.

Statisztika:

23 dolgozat érkezett.
5 pontot kapott:	Baumgartner Róbert, Bogár Blanka, Bősze Zsuzsanna, Damásdi Gábor, Dolgos Tamás, Énekes Péter, Földvári Gábor, Frittmann Júlia, Köpenczei Gergő, Máthé László, Nagy Róbert, Schultz Vera Magdolna, Simig Dániel, Szabó 777 Bence, Tekeli Tamás, Weisz Gellért, Zsakó András.
3 pontot kapott:	5 versenyző.
2 pontot kapott:	1 versenyző.

A KöMaL 2011. márciusi matematika feladatai