A B. 4354. feladat (2011. április)

B. 4354. Adottak a síkon az egymástól különböző A, B, C, D pontok. Szerkesszünk két egymást kívülről érintő kört, amelyek egyike az A és B pontokon, másika a C és D pontokon megy át, továbbá érintési pontjuk rajta van a BC szakaszon.

(4 pont)

A beküldési határidő 2011. május 10-én LEJÁRT.

Megoldás. Az \(\displaystyle A\) és \(\displaystyle B\) pontokon átmenő kört jelölje \(\displaystyle k_1\), a másikat \(\displaystyle k_2\), a \(\displaystyle k_i\) kör középpontját \(\displaystyle O_i\), a két kör érintési pontját pedig \(\displaystyle E\).

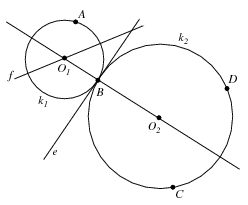
Először vizsgáljuk meg azt az esetet, amikor az \(\displaystyle E\) pont egybeesik a \(\displaystyle BC\) szakasz valamelyik végpontjával. Az \(\displaystyle E=B\) eset csak akkor fordulhat elő, ha a \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) pontok nem esnek egy egyenesre. Ekkor szerkesszük meg a \(\displaystyle k_2=BCD\) kört és annak \(\displaystyle O_2\) középpontját, továbbá a \(\displaystyle k_2\) kört \(\displaystyle B\)-ben érintő \(\displaystyle e\) egyenest. A feladatnak pontosan akkor lesz ilyen megoldása, ha az \(\displaystyle e\) egyenes elvásztja az \(\displaystyle A\) pontot a \(\displaystyle C,D\) pontoktól. Ha ez teljesül, akkor a megoldás egyértelmű lesz: az \(\displaystyle O_1\) pontot az \(\displaystyle O_2B\) egyenesnek és az \(\displaystyle AB\) szakasz \(\displaystyle f\) felező merőlegesének metszéspontjaként kapjuk meg. A \(\displaystyle E=C\) eset hasonlóképpen vizsgálható meg.

A továbbiakban azokat a megoldásokat keressük, ahol az \(\displaystyle E\) pont a \(\displaystyle BC\) szakasz belső pontja. Ha az \(\displaystyle A,D\) pontok közül valamelyik a \(\displaystyle BC\) egyenesre esik, akkor az egybe kell essen az \(\displaystyle E\) ponttal. Ez azt jelenti, hogy ha az \(\displaystyle A\), \(\displaystyle D\) pontok közül valamelyik a \(\displaystyle BC\) egyenesre esik, akkor csak az egyikük eshet arra, méghozzá a \(\displaystyle BC\) szakasz belső pontjaként. Tegyük fel, hogy \(\displaystyle A\) a \(\displaystyle BC\) szakasz belső pontja, de \(\displaystyle D\) nem esik a \(\displaystyle BC\) egyenesre. Ekkor a fenti eljárás szó szerint alkalmazható, ha abban felcseréljük az \(\displaystyle A\) és \(\displaystyle B\) pontok szerepét, es hasonlóképpen járhatunk el, ha a \(\displaystyle D\) pont a \(\displaystyle BC\) szakasz belső pontja, de \(\displaystyle A\) nem esik a \(\displaystyle BC\) egyenesre.

A továbbiakban tehát azt is feltesszük, hogy sem az \(\displaystyle A\), sem a \(\displaystyle D\) pont nem esik a \(\displaystyle BC\) egyenesre. Két esetet kell megkülönböztetnünk aszerint, hogy az \(\displaystyle A\), \(\displaystyle D\) pontok a \(\displaystyle BC\) egyenesnek ugyanarra az oldalára esnek, avagy nem.

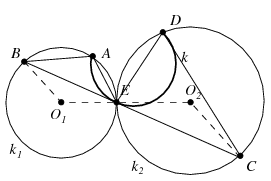
Mivel az \(\displaystyle E\) pont az \(\displaystyle O_1O_2\) szakasz belső pontja, a \(\displaystyle BO_1E\) és \(\displaystyle EO_2C\) irányított szögek egymást \(\displaystyle 360^\circ\)-ra egészítik ki. A kerületi szögek tétele alapján az első esetben ez azt jelenti, hogy az \(\displaystyle EAB\) és \(\displaystyle CDE\) szögek egymást \(\displaystyle 180^\circ\)-ra egészítik ki. Figyelembe véve, hogy az \(\displaystyle ABE\) és \(\displaystyle DEC\) háromszögek szögösszege, valamint a \(\displaystyle BEC\) egyenesszög nagysága is \(\displaystyle 180^\circ\), ez azt jelenti, hogy az \(\displaystyle AED\) irányított szög megegyezik az \(\displaystyle ABC\) és \(\displaystyle BCD\) irányított szögek összegével, ami kisebb kell legyen \(\displaystyle 180^\circ\)-nál, vagyis az \(\displaystyle E\) pont egy, az \(\displaystyle AD\) húr fölé szerkesztett \(\displaystyle k\) látóköríven helyezkedik el. Ez a feltétel könnyen láthatóan elégséges is, az \(\displaystyle E\) pont ismeretében pedig a két kör már könnyen megszerkeszthető.

Így 2, 1 vagy 0 megoldás adódik, annak megfelelően, hogy a \(\displaystyle k\) körívnek és a \(\displaystyle BC\) szakasznak hány közös belső pontja van.

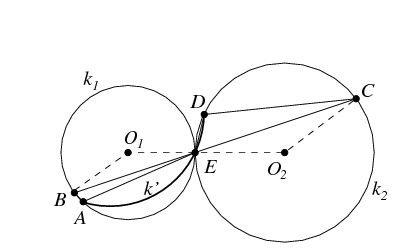
Végül vizsgáljuk azt az esetet, amikor a \(\displaystyle BC\) egyenes elválasztja az \(\displaystyle A\) és \(\displaystyle B\) pontokat. Az egyszerűség kedvéért tegyük fel, hogy \(\displaystyle CBA\angle\ge BCD\angle\). Ha itt egyenlőség áll, vagyis a \(\displaystyle BA\) és \(\displaystyle CD\) egyenesek párhuzamosak egymással, akkor világos, hogy a keresett \(\displaystyle E\) pont a \(\displaystyle BC\) és \(\displaystyle AD\) szakaszok metszéspontja lesz. Legyen tehát \(\displaystyle CBA\angle> BCD\angle\). Mivel ebben az esetben \(\displaystyle BAE\angle=CDE\angle\), azt kapjuk, hogy \(\displaystyle DEC\angle-AEB\angle=CBA\angle- BCD\angle\), vagyis

\(\displaystyle AED\angle=(180^\circ-DEC\angle)+AEB\angle=180^\circ-(CBA\angle- BCD\angle),\)

tehát az \(\displaystyle E\) pont ismétcsak egy, az \(\displaystyle AD\) húr fölé szerkesztett \(\displaystyle k'\) látóköríven helyezkedik el. Nem nehéz meggondolni, hogy a \(\displaystyle k'\) ívnek és a \(\displaystyle BC\) szakasznak pontosan egy közös belső pontja lesz, ami a keresett \(\displaystyle E\) pontot szolgáltatja.

Statisztika:

15 dolgozat érkezett.
4 pontot kapott:	Kabos Eszter, Weimann Richárd.
3 pontot kapott:	Bálint Csaba, Gyarmati Máté, Medek Ákos, Weisz Gellért.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2011. áprilisi matematika feladatai