A B. 4393. feladat (2011. november)

B. 4393. Egy szabályos háromszögnek kiválasztottuk a csúcsait, a középpontját és az oldalainak harmadolópontjait. Hány pontot tarthatunk meg közülük úgy, hogy semelyik három ne alkosson szabályos háromszöget?

Javasolta: Demeter Albert (Matlap, Kolozsvár)

(4 pont)

A beküldési határidő 2011. december 12-én LEJÁRT.

Megoldás. Ha valamelyik oldalról megtartottuk mind a 4 pontot, akkor egyetlen további pontot sem tarthatunk meg. Ha valamelyik oldalról pontosan 3 pontot tartottunk meg, akkor szimmetria okok miatt feltehetjük, hogy ezek az \(\displaystyle A,B,C\) vagy az \(\displaystyle A,B,D\) pontok. Az első esetben \(\displaystyle D\)-n kívül az \(\displaystyle E,F,H\) pontokat sem tarthatjuk meg, a \(\displaystyle G,I,J\) pontokat viszont igen. Tehát ebben az esetben 6 pont megtartható, de több nem. A másik esetben \(\displaystyle C\)-n kívül az \(\displaystyle E,I,J\) pontokat sem tarthatjuk meg, a \(\displaystyle G,H\) pontok közül pedig legfeljebb egyet tarthatunk meg, tehát összesen legfeljebb 5 pontot.

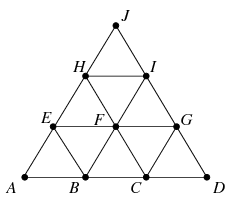
Most megmutatjuk, hogy úgy is csak legfeljebb 5 pontot tarthatunk meg, ha minden oldalról legfejebb kettőt tartunk meg, ami azt jelenti, hogy a feladat kérdésére legfeljebb hatot a helyes válasz. Ez nyilvánvaló, ha a megtartott pontok között két csúcs is szerepel, mert akkor az oldalakról összesen legfeljebb két további pont tartható meg. Az az eset is könnyen meggondolható, ha egyetlen csúcsot sem tartunk meg, ugyanis mind a \(\displaystyle C,E,I\), mind a \(\displaystyle B,G,H\) hármasból legfeljebb két pont tartható meg. Marad az az eset, amikor pontosan egy csúcsot tartunk meg, legyen ez \(\displaystyle J\), az \(\displaystyle A,D\) pontokat ekkor nem tarthatjuk meg. A \(\displaystyle H,I\) pontok közül legfeljebb egyet tarthatunk meg, az \(\displaystyle E,G\) pontok közül úgyszintén. Végül a \(\displaystyle B,C,F\) pontok közül legfeljebb kettő tartható meg, ami összesen valóban legfeljebb 5 pont megtartását jelenti.

Statisztika:

213 dolgozat érkezett.
4 pontot kapott:	101 versenyző.
3 pontot kapott:	21 versenyző.
2 pontot kapott:	29 versenyző.
1 pontot kapott:	36 versenyző.
0 pontot kapott:	26 versenyző.

A KöMaL 2011. novemberi matematika feladatai