A B. 4448. feladat (2012. április)

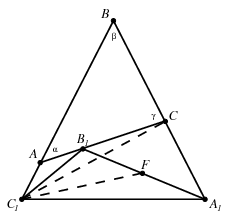
B. 4448. Az ABC háromszög AC oldalához tartozó hozzáírt köre a BC, AC és AB oldalegyeneseket rendre az A₁, B₁ és C₁ pontokban érinti. Legyen F az A₁B₁ szakasz felezőpontja. Igazoljuk, hogy $B_1C_1C \sphericalangle = A_1C_1F \sphericalangle$ .

(4 pont)

A beküldési határidő 2012. május 10-én LEJÁRT.

Megoldás. Tekintsük az AB₁C₁, BA₁C₁ és CA₁B₁ egyenlő szárú háromszögeket. A szokásos jelölésekkel $AB_1C_1\sph=AC_1B_1\sph= \alpha/2$ , $CA_1B_1\sph=CB_1A_1\sph=\gamma/2$ és $BA_1C_1\sph=BC_1A_1\sph= 90^\circ-\beta/2=\alpha/2+\gamma/2$ . Innen kapjuk, hogy $CB_1C_1\sph= 180^\circ-\alpha/2$ , $A_1B_1C_1\sph=180^\circ-\alpha/2-\gamma/2= 90^\circ+\beta/2$ , $B_1A_1C_1\sph=\alpha/2$ , valamint $A_1C_1B_1\sph=\gamma/2<90^\circ$ .

A szinusz-tételt az A₁C₁F és B₁C₁F háromszögekre alkalmazva

$\frac{\sin A_1C_1F\sph}{\sin C_1A_1F\sph}=\frac{A_1F}{C_1F}= \frac{B_1F}{C_1F}=\frac{\sin B_1C_1F\sph}{\sin C_1B_1F\sph}$

adódik, ahonnan

$\frac{\sin A_1C_1F\sph}{\sin B_1C_1F\sph}= \frac{\sin C_1A_1F\sph}{\sin C_1B_1F\sph}= \frac{\sin \alpha/2}{\sin (90^\circ+\beta/2)}.$

Ugyanezt az A₁C₁C és B₁C₁C háromszögekre elvégezve a

$\frac{\sin A_1C_1C\sph}{\sin C_1A_1C\sph}=\frac{A_1C}{C_1C}= \frac{B_1C}{C_1C}=\frac{\sin B_1C_1C\sph}{\sin C_1B_1C\sph},$

$\frac{\sin A_1C_1C\sph}{\sin B_1C_1C\sph}= \frac{\sin C_1A_1C\sph}{\sin C_1B_1C\sph}= \frac{\sin (90^\circ-\beta/2)}{\sin (180^\circ-\alpha/2)}$

összefüggéseket kapjuk. Mivel sin (90^o+ $\beta$ /2)=sin (90^o- $\beta$ /2) és sin (180^o- $\alpha$ /2)=sin $\alpha$ /2, végül

$\frac{\sin A_1C_1F\sph}{\sin B_1C_1F\sph}= \frac{\sin B_1C_1C\sph}{\sin A_1C_1C\sph}.$

Figyelembe véve, hogy

$A_1C_1C\sph+B_1C_1C\sph=B_1C_1F\sph+A_1C_1F\sph= A_1C_1B_1\sph<90^\circ$

és hogy a (0,90^o) intervallumon a $\sin x/\sin({A_1C_1B_1\sph}-x)$ függvény szigorúan monoton növekedő, ebből éppen a bizonyítandó állítást kapjuk.

Statisztika:

21 dolgozat érkezett.

4 pontot kapott: Ágoston Tamás, Bingler Arnold, Fehér Zsombor, Forrás Bence, Havasi 0 Márton, Janzer Olivér, Medek Ákos, Mester Márton, Nagy Anna Noémi, Ódor Gergely, Strenner Péter, Szabó 789 Barnabás, Szabó 928 Attila.

3 pontot kapott: Bősze Zsuzsanna, Gyarmati Máté, Nagy Róbert.

2 pontot kapott: 2 versenyző.

1 pontot kapott: 3 versenyző.

A KöMaL 2012. áprilisi matematika feladatai

21 dolgozat érkezett.
4 pontot kapott:	Ágoston Tamás, Bingler Arnold, Fehér Zsombor, Forrás Bence, Havasi 0 Márton, Janzer Olivér, Medek Ákos, Mester Márton, Nagy Anna Noémi, Ódor Gergely, Strenner Péter, Szabó 789 Barnabás, Szabó 928 Attila.
3 pontot kapott:	Bősze Zsuzsanna, Gyarmati Máté, Nagy Róbert.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	3 versenyző.

Már regisztráltál?
Új vendég vagy?