A B. 4485. feladat (2012. november)

B. 4485. Legfeljebb mekkora részét fedheti le egy háromszögnek egy olyan négyzet, amelynek minden csúcsa a háromszög valamelyik oldalán van?

Javasolta: Légrádi Imre (Sopron)

(4 pont)

A beküldési határidő 2012. december 10-én LEJÁRT.

Útmutatás: Határozzuk meg a négyzetek oldalát.

Megoldás: A négyzet csúcsai az ABC háromszög oldalain az ábrán látható módon helyezkednek el azzal a megjegyzéssel, hogy az X csúcs egybeeshet A-val (vagy az Y csúcs B-vel).

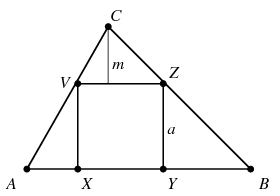
A négyzet oldalának hosszát jelölje a, a VZC háromszög VZ oldalhoz tartozó magasságát m. Az (esetleg elfajuló) AXV és YBZ háromszögeket egymás mellé tolva egy olyan, a VZC háromszöghöz hasonló, vele egyállású háromszöget kapunk, melynek m-mel párhuzamos magassága XV=YZ=a, alapja pedig ennek megfelelően a²/m. A négyzet által az ABC háromszögből levágott 3 kis háromszög területének összege tehát a számtani-mértani egyenlőtlenség szerint

$\frac{1}{2}\left(am+\frac{a^2}{m}\cdot a\right)\ge \sqrt{am\cdot\frac{a^2}{m}\cdot a}=\sqrt{a^4}=a^2,$

ahol a² éppen az XYZV négyzet területe. A négyzet tehát az ABC háromszög területének legfeljebb a felét fedheti le, ahol egyenlőség pontosan az a=m esetben áll fenn, vagyis ha a háromszög egyik magasságának hossza megegyezik a hozzá tartozó alap hosszával, és a négyzet egyik oldala erre az alapra esik.

Statisztika:

152 dolgozat érkezett.

4 pontot kapott: Árkos Gergely, Balogh Tamás, Barna István, Bingler Arnold, Bognár Máté, Boguszlavszkij Gergely, Bősze Zsuzsanna, Csernák Tamás, Czipó Bence, Di Giovanni Márk, Fehér Zsombor, Fekete Panna, Fonyó Viktória, Forrás Bence, Havasi 0 Márton, Janzer Barnabás, Janzer Olivér, Jenei Adrienn, Kabos Eszter, Kaprinai Balázs, Kátay Tamás, Khayouti Sára, Kovács 101 Dávid Péter, Leitereg András, Maga Balázs, Medek Ákos, Nagy Bence Kristóf, Nagy Gergely, Németh Gergely, Petrényi Márk, Porupsánszki István, Qian Lívia, Sagmeister Ádám, Schultz Vera Magdolna, Schwarcz Tamás, Seress Dániel, Simon Kristóf, Szabó 262 Lóránt, Szaksz Bence, Szebellédi Márton, Szőke Tamás, Varga 149 Imre Károly, Varga 911 Szabolcs, Venczel Tünde, Weisz Ambrus, Zilahi Tamás.

3 pontot kapott: 60 versenyző.

2 pontot kapott: 17 versenyző.

1 pontot kapott: 16 versenyző.

0 pontot kapott: 13 versenyző.

A KöMaL 2012. novemberi matematika feladatai

152 dolgozat érkezett.
4 pontot kapott:	Árkos Gergely, Balogh Tamás, Barna István, Bingler Arnold, Bognár Máté, Boguszlavszkij Gergely, Bősze Zsuzsanna, Csernák Tamás, Czipó Bence, Di Giovanni Márk, Fehér Zsombor, Fekete Panna, Fonyó Viktória, Forrás Bence, Havasi 0 Márton, Janzer Barnabás, Janzer Olivér, Jenei Adrienn, Kabos Eszter, Kaprinai Balázs, Kátay Tamás, Khayouti Sára, Kovács 101 Dávid Péter, Leitereg András, Maga Balázs, Medek Ákos, Nagy Bence Kristóf, Nagy Gergely, Németh Gergely, Petrényi Márk, Porupsánszki István, Qian Lívia, Sagmeister Ádám, Schultz Vera Magdolna, Schwarcz Tamás, Seress Dániel, Simon Kristóf, Szabó 262 Lóránt, Szaksz Bence, Szebellédi Márton, Szőke Tamás, Varga 149 Imre Károly, Varga 911 Szabolcs, Venczel Tünde, Weisz Ambrus, Zilahi Tamás.
3 pontot kapott:	60 versenyző.
2 pontot kapott:	17 versenyző.
1 pontot kapott:	16 versenyző.
0 pontot kapott:	13 versenyző.

Már regisztráltál?
Új vendég vagy?