 |
A B. 4495. feladat (2012. december) |
B. 4495. Adott az ABCD parallelogramma, valamint az F és a G pontok, melyekre teljesül, hogy AF=FC, BG=GD, továbbá az AFC és a BGD háromszögek hasonlóak. Mutassuk meg, hogy az FG egyenes merőleges a parallelogramma egyik oldalára.
Javasolta: Miklós Szilárd (Herceghalom)
(5 pont)
A beküldési határidő 2013. január 10-én LEJÁRT.
Útmutatás: Milyen forgatva nyújtás viszi az AC szakaszt az AF szakaszba? (Kiszámolhatjuk komplex számokkal is.)
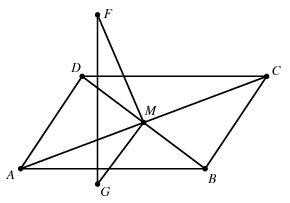
Megoldás: Az átlók metszéspontját jelölje M. Az F pont az AC átló, G pedig a BD átló felező merőlegesén helyezkedik el. Mivel FM:MC=GM:MD, az FMG háromszöget az M pontból alkalmas nagyítással egy olyan F'MG' háromszögbe vihetjük, melyre F'M=MC és G'M=MD. Ekkor F'G' párhuzamos FG-vel, ezért elég azt igazolni, hogy az F'G' egyenes merőleges a parallelogramma egyik oldalára. Másképp fogalmazva, elegendő a feladat állítását az FM=MC, GM=MD feltétel mellett bizonyítani.
Szimmetria okok miatt elég két esetet megkülönböztetni. Az egyik eset látható az ábrán, a másik esetben G helyett annak M-re vett tükörképével kell dolgozni. Az ábrán látható esetben az FMG háromszöget megkaphatjuk a CMD háromszögből, azt M körül pozitív irányban 90o-os szöggel elforgatva. Ezért ekkor FG merőleges a CD oldalra. A másik esetben az FMG háromszöget úgy kapjuk meg, hogy az AMD háromszöget forgatjuk el M körül negatív irányban 90o-os szöggel, így ekkor FG az AD oldalra lesz merőleges.
Statisztika:
114 dolgozat érkezett. 5 pontot kapott: 73 versenyző. 4 pontot kapott: 36 versenyző. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2012. decemberi matematika feladatai
