 |
A B. 4498. feladat (2012. december) |
B. 4498. Azt mondjuk, hogy az ABCD konvex négyszög B csúcsa ,,különleges'', ha a BD egyenesnek az ABC szög felezőjére vett tükörképe felezi az AC átlót. Bizonyítsuk be, hogy ha egy húrnégyszög valamelyik csúcsa különleges, akkor minden csúcsa az.
Javasolta: Maga Péter
(5 pont)
A beküldési határidő 2013. január 10-én LEJÁRT.
Útmutatás: Legyen F az AC szakasz felezőpontja. Írjuk fel a szinusztételt az ABF és a BCF háromszögekre.
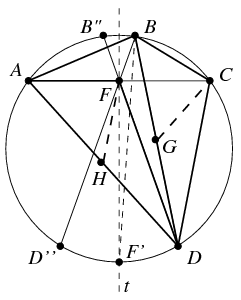
Megoldás: Elegendő annyit belátni, hogy ha a B csúcs különleges, akkor az A csúcs is az. Az AC, BD és AD szakaszok felezőpontját jelölje rendre F, G, illetve H. Legyen az AC szakasz felező merőlegese t. A B,D pontok t-re vett tükörképét jelölje B'',D'', továbbá legyen F' a t egyenesnek a B-t nem tartalmazó AC ívvel vett metszéspontja. Ekkor F' az AC ív felezőpontja, vagyis az a pont, amelyben a B-ből induló szögfelező az AC ívet metszi.
Az hogy a B csúcs különleges, ekvivalens tehát azzal, hogy a BD'' és B''D szakaszok áthaladnak az F ponton, vagyis hogy a CDB szög egyenlő az FDA szöggel. Az ,
,
megfeleltetés szerint pedig az A csúcs különleges volta ekvivalens azzal, hogy a DCA szög egyenlő az GCB szöggel. Annyit kell ezek szerint csak belátnunk, hogy ha CDB
 =FDA
=FDA , akkor DCA
, akkor DCA =GCB
=GCB is teljesül.
is teljesül.
Tegyük fel tehát, hogy CDB =FDA
=FDA . Mivel a kerületi szögek tétele szerint DBC
. Mivel a kerületi szögek tétele szerint DBC =DAF
=DAF , a DBC és DAF háromszögek hasonlóak. Ezért a GBC és HAF háromszögek is hasonlóak. Mivel pedig az FH szakasz párhuzamos CD-vel, látható hogy valóban GCB
, a DBC és DAF háromszögek hasonlóak. Ezért a GBC és HAF háromszögek is hasonlóak. Mivel pedig az FH szakasz párhuzamos CD-vel, látható hogy valóban GCB =HFA
=HFA =DCA
=DCA .
.
Statisztika:
30 dolgozat érkezett. 5 pontot kapott: Balogh Tamás, Bingler Arnold, Bogár Blanka, Bősze Zsuzsanna, Emri Tamás, Fehér Zsombor, Gyulai-Nagy Szuzina, Janzer Barnabás, Janzer Olivér, Kúsz Ágnes, Maga Balázs, Nagy-György Pál, Paulovics Zoltán, Petrényi Márk, Sagmeister Ádám, Simkó Irén, Simon 047 Péter, Szabó 789 Barnabás, Szabó 928 Attila, Tossenberger Tamás, Venczel Tünde. 4 pontot kapott: Dinev Georgi, Herczeg József, Kabos Eszter, Medek Ákos, Nagy Róbert, Schultz Vera Magdolna. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2012. decemberi matematika feladatai
