 |
A B. 4499. feladat (2012. december) |
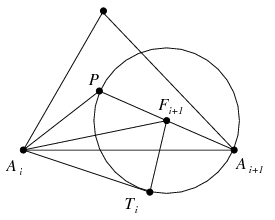
B. 4499. Legyen P az A1A2A3 hegyesszögű háromszög belső pontja. A Ti pontokat úgy vesszük fel, hogy az AiTi szakasz Ti-ben érintse a PAi+1 átmérőjű kört (i=1,2,3, A4=A1). Mutassuk meg, hogy
Javasolta: Péter Árpád (Sepsiszentgyörgy) (Matlap, Kolozsvár)
(4 pont)
A beküldési határidő 2013. január 10-én LEJÁRT.
Útmutatás: Vetítsük a P pontot az oldalakra.
Megoldás: Az PAi szakasz felezőpontját, vagyis a PAi átmérőjű kör középpontját jelölje Fi. Az AiTiFi+1 derékszögű háromszögből
2AiTi2=2(AiFi+12-TiFi+12)=2AiFi+12-2Ai+1Fi+12.
Mivel pedig AiFi+1 a PAiAi+1 háromszög súlyvonala,
AiAi+12+AiP2=2AiFi+12+2Ai+1Fi+12.
Ezek alapján
2AiTi2=AiAi+12+AiP2-4Ai+1Fi+12=AiAi+12+AiP2-Ai+1P2.
Ezt i=1,2,3 esetén összegezve a bizonyítandó egyenlőséget kapjuk.
Statisztika:
46 dolgozat érkezett. 4 pontot kapott: Ágoston Péter, Balogh Tamás, Barna István, Bereczki Zoltán, Bingler Arnold, Bogár Blanka, Boguszlavszkij Gergely, Bősze Zsuzsanna, Demeter Dániel, Di Giovanni Márk, Emri Tamás, Fehér Zsombor, Fonyó Viktória, Forrás Bence, Győrfi 946 Mónika, Janzer Barnabás, Janzer Olivér, Kabos Eszter, Kovács Balázs Marcell, Lelkes János, Maga Balázs, Medek Ákos, Nagy Bence Kristóf, Nagy-György Pál, Paulovics Zoltán, Petrényi Márk, Porupsánszki István, Qian Lívia, Sagmeister Ádám, Sal Kristóf, Sárosdi Zsombor, Schultz Vera Magdolna, Schwarcz Tamás, Simon 047 Péter, Stein Ármin, Sütő Máté, Szabó 524 Tímea, Szabó 789 Barnabás, Szabó 928 Attila, Szőke Tamás, Tóth 095 Zsombor, Varga 911 Szabolcs, Venczel Tünde, Vető Bálint, Wiandt Péter, Zilahi Tamás.
A KöMaL 2012. decemberi matematika feladatai
