 |
A B. 4504. feladat (2013. január) |
B. 4504. Egy derékszögű háromszögben az átfogó felezőmerőlegesének a befogók egyenesei közé eső szakasza ugyanolyan hosszú, mint az átfogó. Mekkorák a háromszög szögei?
(4 pont)
A beküldési határidő 2013. február 11-én LEJÁRT.
Megoldási ötlet: Keressünk egyenlő szárú háromszögeket.
Megoldás. Legyen a háromszög átfogója AB, derékszögű csúcsa C, az átfogó felezőpontja F, a befogók egyenesei és az átfogó felező merőlegesének metszéspontja P, illetve Q, az ábra szerint. Legyen .
Mivel P az AB felező merőlegesén van, . Az ABC és a QBF derékszögű háromszögek hasonlók, mert B-nél levő szögük közös, ezért
. Az ABC és a QPC háromszögek is hasonlók, mert két szögük megegyezik.
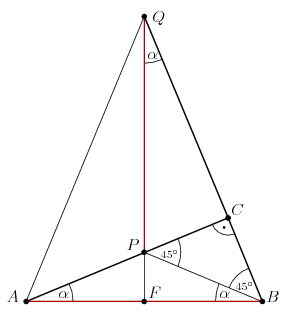
Az ABC és a QPC derékszögű háromszögek átfogója egyenlő, ezért a két háromszög egybevágó; többek közt BC=PC. A BPC háromszög tehát egyenlő szárú derékszögű háromszög, és . (Hasonlóan láthatjuk, hogy AC=QC, és az ACQ háromszög is egyenlő szárú derékszögű háromszög.) Ezután az ABC háromszög szögeiből leolvashatjuk, hogy
 =22,5o.
=22,5o.
A lépéseink megfordíthatóak: ha  =22,5o, akkor
=22,5o, akkor , az ABC és a QPC háromszögek egybevágók, végül AB=PQ.
Az ABC háromszög szögei tehát 90o, 22,5o és 67,5o.
Statisztika:
205 dolgozat érkezett. 4 pontot kapott: 129 versenyző. 3 pontot kapott: 53 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 14 versenyző.
A KöMaL 2013. januári matematika feladatai
