 |
A B. 4510. feladat (2013. január) |
B. 4510. Az O középpontú szabályos (2k+1)-szög alapú egyenes gúla alapéleinek hossza 1, OB magasságának hossza pedig m. Tükrözzük a gúlát az OB szakasz felezőpontjára. Mekkora a két gúla közös részének a térfogata?
(6 pont)
A beküldési határidő 2013. február 11-én LEJÁRT.
Megoldási ötlet: A gúlák közös tengelyére illeszkedő félsíkokkal bontsuk részekre a gúlákat és a közös részüket (mint egy tortát), és számítsuk ki a térfogatokat egy-egy szeletben.
Megoldás. Legyen a gúla alaplapja , a tükörkép alaplapja
, csúcsa O. Az alaplapok csúcsait modulo 2k+1 fogjuk indexelni, tehát például A2k+1=A0.
Legyen az AiAi+1 él felezőpontja Fi, a CiCi+1 él felezőpontja pedig Gi. Például az AiFiO derékszögű háromszögekből leolvashatjuk, hogy az alaplapok köré írt kör sugara
a beírt körök sugara pedig
A B, O, Ai és Gk+i pontok egy síkba esnek, mert CiBGk+i =180o; legyen Ui=AiB
=180o; legyen Ui=AiB Gk+iO. Hasonlóan legyen Vi=FiB
Gk+iO. Hasonlóan legyen Vi=FiB Ck+i+1O.
Ck+i+1O.
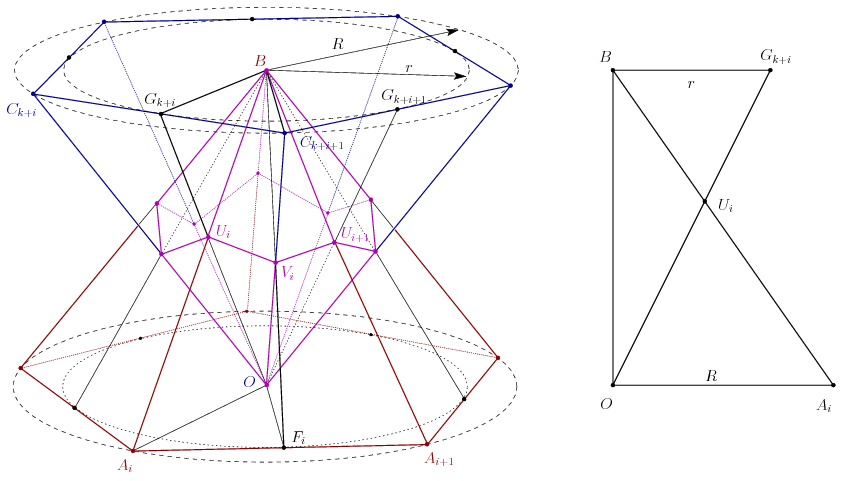
Tekintsük most a gúláknak és a metszetüknek a BOAiGk+i és BOFiCk+i+1 félsíkok közé eső részét. A közös részt a két félsík, továbbá az AiAi+1B és Ck+iCk+i+1O lapok határolják, a közös rész tehát egy tetraéder, amelynek csúcsai B, O, Ui és Vi.
A BOUiVi tetraéder térfogatát a BOAiFi tetraéder térfogatával fogjuk összehasonlítani. A OAiGk+iB derékszögű trapéz alapjainak hossza OAi=R és Gk+iB=r, az átlók metszéspontja Ui. A OAiUi és Gk+iBUi háromszögek hasonlók, így , és
Hasonlóan, a OFiCk+i+1B trapéz vizsgálatából kapjuk, hogy
Ezek után
A szimmetria miatt az arány mindegyik térrészben ugyanaz. Ezért a két gúla közös részének térfogata
Statisztika:
27 dolgozat érkezett. 6 pontot kapott: Balogh Tamás, Fehér Zsombor, Forrás Bence, Havasi 0 Márton, Janzer Olivér, Maga Balázs, Schwarcz Tamás, Tardos Jakab, Tossenberger Tamás, Venczel Tünde. 5 pontot kapott: Ágoston Péter, Herczeg József, Lelkes János, Medek Ákos, Németh Gergely, Paulovics Zoltán, Simkó Irén, Szabó 789 Barnabás. 4 pontot kapott: 3 versenyző. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 4 versenyző.
A KöMaL 2013. januári matematika feladatai
