Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A B. 4523. feladat (2013. március)

B. 4523. Egy szimmetrikus trapézban az átlók merőlegesek egymásra. Mekkora lehet a trapéz kerületének és középvonalának aránya?

Javasolta: Kovács Béla (Szatmárnémeti)

(4 pont)

A beküldési határidő 2013. április 10-én LEJÁRT.

Megoldási ötlet: Rajzoljuk meg a szárak felezőpontja és az átlók metszéspontja által meghatározott háromszöget.

1. megoldás. Betűzük a négyszög csúcsait az ábra szerint; legyen E és F a BC, illetve az AD szár felezőpontja és M az átlók metszéspontja.

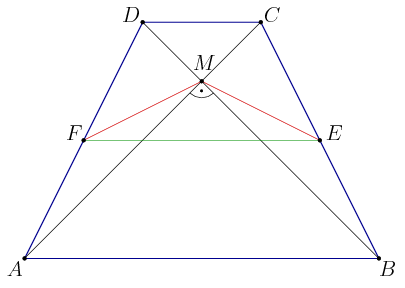
A trapézban az EF középvonal az AB és CD alapok átlaga:

EF = \frac{AB+CD}{2}

A feltétel szerint az átlók merőlegesek, ezért a BCM háromszög derékszögű. A derékszögű háromszög köré írt kör középpontja az átfogó felezőpontja, E. Tehát

EM=\frac{BC}{2} és hasonlóan FM=\frac{AD}{2}.

Ezért

\frac{ker\ddot{u}let}{k\ddot{o}z\acute{e}pvonal} = \frac{AB+BC+CD+DA}{EF} = \frac{2EF+2EM+2FM}{EF} = 2+4\frac{EM}{EF}.

Az FEM (esetleg szakasszá elfajuló) egyenlő szárú háromszög csúcsszöge tompaszög, alapon fekvő szögei 45o-nál kisebbek. Ezért

\frac12 \le \frac{EM}{EF} = \frac1{2\cos FEM\angle} < \frac1{2\cos 45^\circ} = \frac{\sqrt{2}}2 ,

tehát

4 \le \frac{ker\ddot{u}let}{k\ddot{o}z\acute{e}pvonal} < 2+2\sqrt2 . (*)

Végük vázoljuk, annak igazolását, hogy ezek az értékek mind lehetségesek. Ehhez elegendő azt ellenőriznünk, hogy az ábra rekonstruálható tetszőleges olyan egyenlő szárú FEM (esetleg elfajuló) hármszögből, amelyben FEM\angle<45o.

Vegyünk egy tetszőleges ilyen FEM háromszöget. Húzzuk meg M-en kereszül azt az e és f egyenest, amely EF-fel 45o-os szöget zár be; ezek lesznek az átlók egyenesei. Az e és f egyenesek a síkot négy részre osztják; mivel EMF\angle>90o, az E és F pontok egymással szemközti síknegyedekben vannak. A két síknegyed határán vegyük fel azokat A, B, C, D pontokat, amelyekre az AMF, BME, CME, DMF háromszögek egyenlő szárúak; mivel BEM\angle+MEC\angle=2CME\angle+2EMB\angle=180o, a B,E,C pontok egy egyenesre esnek. Hasonlóan kapjuk, hogy az A,F,D pontok is egyenesre esnek. A szimmetria miatt az ABCD négyszög szimmetrikus trapéz.

Megjegyzés. A (*) becslés levezetése minimális módosítással akkor is elmondató, ha a trapéz nem szimmetrikus.

2. megoldás (vázlat). Használjuk az 1. megoldás jelöléseit, legyen MA=MB=x>0 és MC=MD=y>0. ekkor

\frac{ker\ddot{u}let}{k\ddot{o}z\acute{e}pvonal} = \frac{AB+BC+CD+DA}{\frac12(AB+CD)} = \frac{\sqrt2x + \sqrt{x^2+y^2} +\sqrt2y +\sqrt{x^2+y^2}}{ \frac{\sqrt2}2(x+y)} =

= 2+2\sqrt2\sqrt{\frac{x^2+y^2}{(x+y)^2}} = 2+2\sqrt{1+\left(\frac{|x-y|}{x+y}\right)^2}.

Mivel 0\le|x-y|<x+y,

4\le 2+2\sqrt{1+\left(\frac{|x-y|}{x+y}\right)^2} < 2+2\sqrt2.

A \frac{|x-y|}{x+y} kifejezés tetszőleges, 1-nél kisebb nemnegatív értéket felvehet, ezért a \left[4,2+2\sqrt2\right) intervallumban minden érték lehetséges.

Statisztika:

114 dolgozat érkezett.
4 pontot kapott:Balogh Dániel, Balogh Tamás, Bereczki Zoltán, Bingler Arnold, Bogár Blanka, Csépai András, Csurgai-Horváth Bálint, Di Giovanni Márk, Fekete Panna, Forrás Bence, Janzer Barnabás, Janzer Olivér, Kabos Eszter, Khayouti Sára, Kovács 972 Márton, Lajos Hanka, Maga Balázs, Mezősi Máté, Nagy Gergely, Nagy-György Pál, Németh Gergely, Osváth Tibor Attila, Sagmeister Ádám, Sal Kristóf, Schwarcz Tamás, Szabó 789 Barnabás, Szabó 928 Attila, Szász Dániel Soma, Tóth László Gábor, Venczel Tünde, Vető Bálint, Weisz Ambrus, Zilahi Tamás.
3 pontot kapott:24 versenyző.
2 pontot kapott:20 versenyző.
1 pontot kapott:25 versenyző.
0 pontot kapott:9 versenyző.
Nem versenyszerű:3 dolgozat.

A KöMaL 2013. márciusi matematika feladatai